#Puzzle: What if I told you that the North Pole isn't the only place on Earth from which you can walk 1km due south, turn and walk 1km due east, turn again and walk 1km due north and find yourself back where you started? Where is this other mysterious place? Or places? How many?
There's an old riddle about this. An explorer walks 1km S + 1km E + 1km N, gets back to the starting point and sees a bear. What colour is the bear? The standard answer is white, because the North Pole has this property. The journey would look something like this (not to scale). 
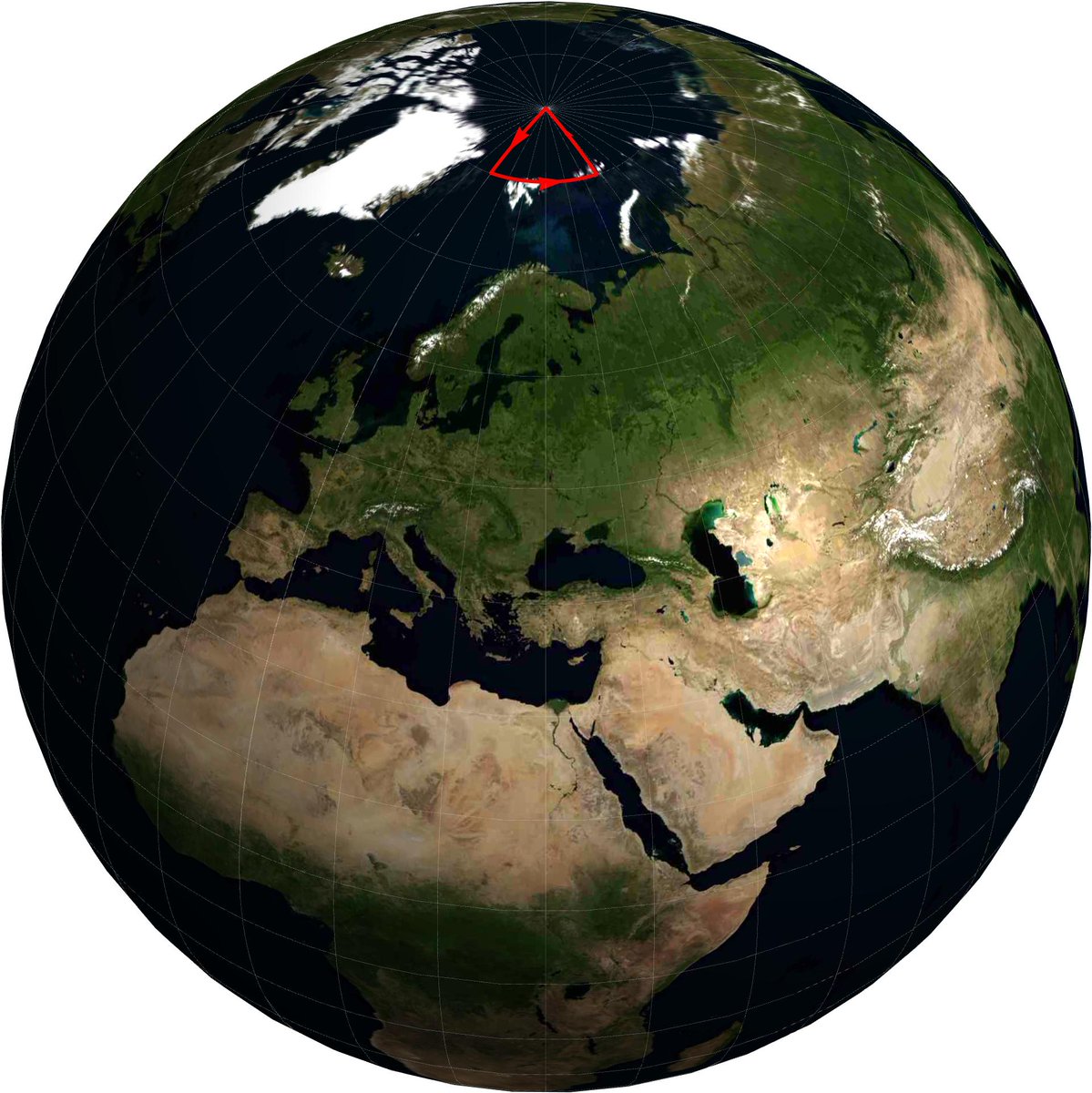
Solution. Take any point on a circle of latitude from which going 1km S lands you on a circle of latitude with circumference 1/M km (M=1,2,3,..). Then go around that smaller circle M times due east. Finally, go 1km N and you're back where you started. (Image not to scale.) 

• • •
Missing some Tweet in this thread? You can try to
force a refresh












