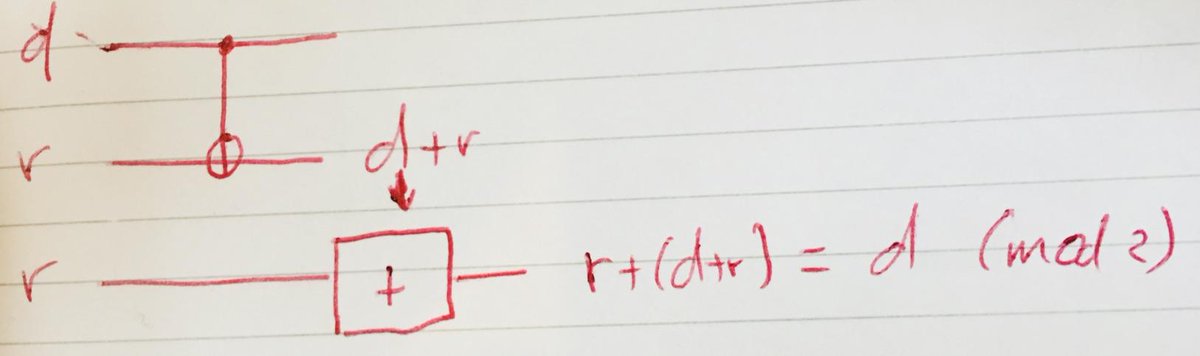Thread by @michael_nielsen

When trying to understand a scientific or mathematical result, I often find it helpful to write what I call discovery fiction.

Discovery fiction is a plausible story of how someone could have discovered a result - a reasonable path of small ideas, false starts, backtracking, and incremental improvement, eventually leading to the result.

Of course, it IS fiction. Such stories shouldn't be taken too seriously - genuine discovery is very different. But I nonetheless find writing discovery fiction useful as a way of helping me understand results more deeply than I otherwise would. It's often a fun form to read, too.

So, how could one discover quantum teleportation? Here's a very abbreviated piece of discovery fiction as a (not entirely serious) answer to that question!

(If you'd like follow along in detail, you may find it helpful to read @andy_matuschak's and my essay: quantum.country/qcvc Testimonial: x.com/KeithMansfield… But you can also just follow along in gist!)

The basic job for teleportation is for Alice to transmit an unknown quantum state a|0>+b|1> to Bob, without directly sending the quantum state or any quantum system.

Coming to this for the first time, you might hope that Alice would be able to measure her state, figure out the quantum amplitudes a and b, and send a classical description of those amplitudes to Bob, who could re-create the state.

Trouble is, it turns out to be impossible to do that in quantum mechanics. It's not just that it's difficult or hard to do, it's genuinely forbidden by the laws of physics!

In fact, in quantum mechanics it turns out that if you acquire information about a state through measurement, that actually damages the state. There's no way round this!

That seems discouraging. But maybe we can tip the problem upside down? Might it be possible for Alice to do a measurement that DOESN'T acquire any information about the amplitudes a and b, but somehow can still help Bob acquire the original state?

That sounds pretty unlikely. But if you know some classical cryptography, you'll know that something like this is done routinely in the cryptosystem known as a one-time pad. Here's how it works.

Alice has a data bit, d, which she'd like to send to Bob. Alice and Bob share a pair of random bits (r, r). Alice XORs d onto her half of the random pair, and sends the result d + r to Bob. Bob can then recover d by adding (d+r) to his random bit: d+(d+r) = d (modulo 2).

The interesting thing for us is that the message d+r from Alice to Bob is completely uncorrelated with the data d. In other words, that message tells us nothing whatsoever about the identity of Alice's data. (This is also why it's cryptographically useful, of course!)

We can draw this in a classical circuit representation as:

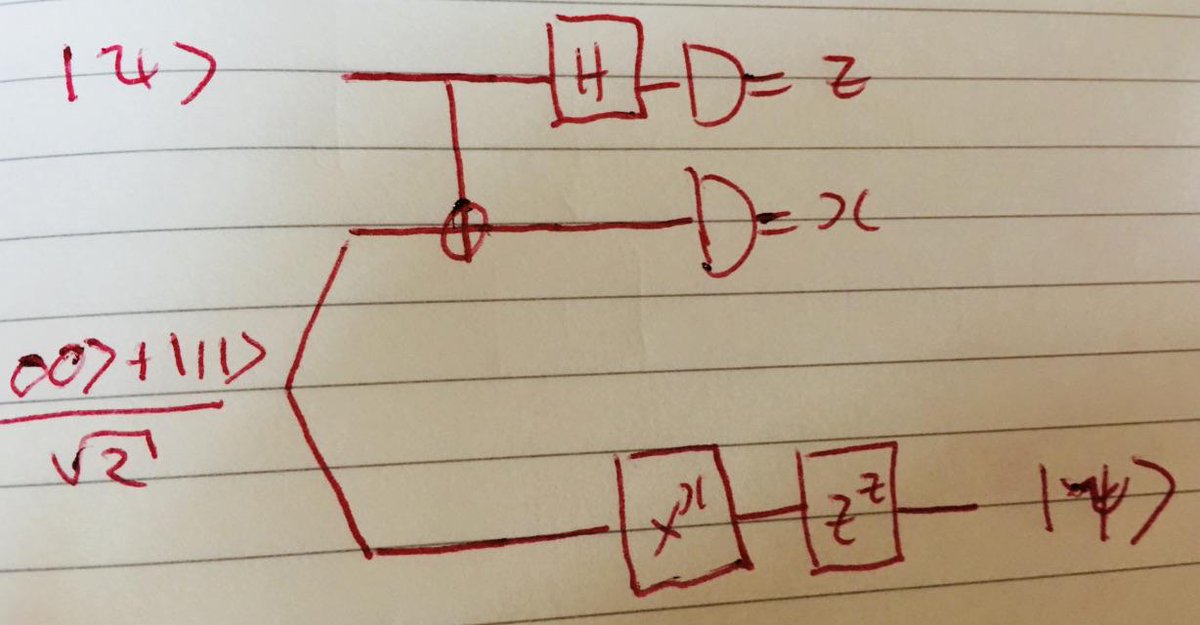
Here's the natural analogous quantum circuit, replacing the random pair of bits (r, r) by the analogous quantum state (|00>+|11>)/(sqrt 2):

Now, you can compute the effect of this circuit mechanically - it's just algebra. I won't go through those details now, though the ideas I
described yesterday
( ) can
be used to verify that if the input is |psi> = a|0>+b|1> then the
output is a|00>+b|11>:

https://x.com/michael_nielsen/status/1131784174203953153

This seems promising: Alice and Bob now share an entangled quantum state with the amplitudes a and b. Can they do something so Bob ends up with the original state a|0>+b|1>?

Unfortunately, Alice can't do it by simply applying a quantum gate - the state will remain entangled. But maybe she can make a measurement of some sort?

Suppose Alice measures her remaining qubit in some basis |m>. The resulting conditional state for Bob is, up to normalization:

a<m|0> |0> + b <m|1> |1>

Ahah! This is very promising! If we simply choose the basis |m> to be the equal superposition states |+> = (|0>+|1>)/sqrt 2 and |-> = (|0>-|1>)/sqrt 2 then Bob will get the following conditional states:

a|0>+b|1>
a|0>-b|1>

That is, Bob's state is just Z^z|psi>, where z is the outcome of a measurement in the |+>, |-> basis.

And so the following quantum circuit teleports |psi> from Alice to Bob:

This is, in fact, the standard quantum teleportation protocol!

This leaves something to be desired as discovery fiction. Still, it's a lot of fun, and think it's pretty good for Twitter!

Particularly egregious: it doesn't tell us WHY you might suspect teleportation is possible in the first place. Though I wonder if some quantum person thinking hard about classical one-time pads might have discovered it, largely by following their nose.

Anyway, this kind of discovery fiction can be a lot of fun, and going through this exercise certainly helped me understand teleportation better!