Algumas coisas são simples de provar, como se a terra é redonda (será? 🤔)
Mostrar isso é mais difícil, pois cada corpo recebe efeitos diferentes quando começam a fazer exercício. Alguns perdem peso mais fácil e outros não.
Analogamente, nossa hipótese nula é o oposto: "exercícios físicos não interferem no peso". Podemos começar pensando que a hipótese nula é verdade
Vamos supor que 10 pessoas fizeram atividade física durante 3 meses.
Ao final, descobrimos que elas perderam em média 3kg, com um desvio padrão de 1kg (as pessoas pouco variam de peso em relação a média)
Acabou? provamos algo?
Só que se, por acaso, o grupo que você testou só perdeu 0,2kg? Você ainda bateria o martelo? Ou acharia que a perda foi insignificante?
Difícil, né?
Um pouco de matemática pode ajudar!
Com probabilidades fica mais fácil entender o que poderá ocorrer no futuro e ter mais certeza sobre o resultado e efeito da pesquisa!
Assim sendo, o p-valor mede a probabilidade de se observar resultados
Nem preciso dizer que para uma pesquisa ser confiável, o p-valor precisa ser muito baixo. Tanto que normalmente o valor que ele assume é abaixo de 0,05
E agora vocês entendem o problema da pesquisa
-Lucas, como calcula?
Então, eu precisaria estudar mais pra fazer um bom vídeo ou texto explicando isso 😅 é bom saber isso, principalmente quando você vai fazer uma pesquisa robusta em Machine Learning!
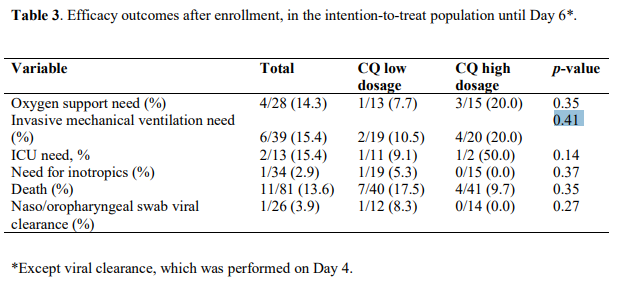
Não manjo muito disso na área médica, mas o p-valor de 0,41 ali parece ser sobre a necessidade de ventilação mecânica usando a cloroquina
De maneira geral os p-valores
mas enfim, não sou médico, só sou um curioso das ciências mesmo =)



