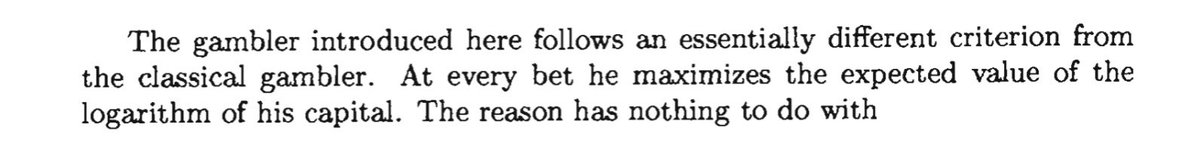In this thread, I'm going to walk you through "The Kelly Criterion".
This is what is now known as the Kelly Criterion.
He also enrolls you in Robinhood's fractional share trading program, but not in margin or options trading.

At the end of 20 years, all the stock in your account will be liquidated, the account will be closed, and its entire value will be given to you in cash.
During this month, ALAD can either double or halve.
So, for every $1 you invest in ALAD at the beginning of the month, you'll have either $2 or $0.50 at the end.
On average, you'll have ($2 + $0.50)/2 = $1.25.
This is beginning to look like a no-brainer.
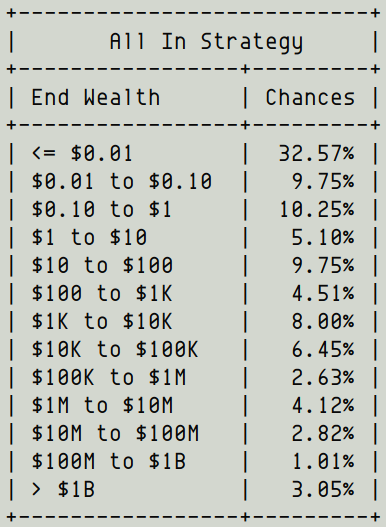
Clearly, the best way to proceed is to go "All In". Put your entire initial $1 in ALAD, and hold it for 20 yrs.
Best case: ALAD doubles every single month. That leaves you with many, many billions of dollars.
Worst case: ALAD gets halved every single month. That leaves you with an insignificant fraction of a penny.
These are like tossing a coin 240 times (once a month for 20 years) and expecting to get heads (or tails) every single time.
So what does the *average* case look like?
Remember that on average, you make 25% per month? Compounded over 20 years, that turns your $1 into many billions.
So, in all likelihood, you'll make out like a bandit, right?
Not so fast.
And a 67.4% chance that you'll end up with less than $100.
And only a 3% chance that you'll end up a billionaire.
It's because outliers skew the average.
The billion dollar plus outcomes are so good that they lift up the entire average.
Kind of like one winning lottery ticket compensating for thousands of duds.
These doublings and halvings cancel each other, leaving you with roughly the same $1 you started with.
*Most likely* outcomes are not swayed by outliers. *Averages* are.
In this case, you will *most likely* end up with just $1. But *on average*, you expect to end up with billions.
You need a strategy that maybe gives up some of the unlikely billions in potential upside, but buys you a very good chance of turning that $1 into $100K or $1M.
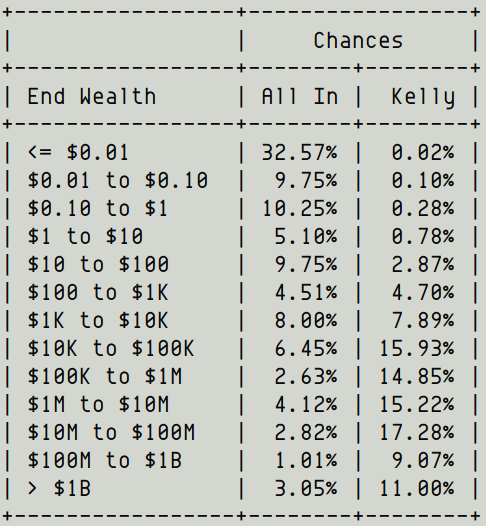
That's the genius of Kelly. He found that strategy.
At the start of each month, rebalance your portfolio so that exactly half of it is in cash and the other half is in ALAD stock.
Kelly also gives you a 50+% chance of ending up a millionaire, and a 11% chance of ending up a billionaire!
The *average* outcome is still in the many billions, although Kelly does sacrifice some of the tail-end mega-billions.
When you apply the math to this particular problem, it so happens that you get 1/2 and 1/2 as the optimal strategy.
What if ALAD could quadruple, double, stay the same, or halve?
What if there was more than 1 stock: Aladdin Enterprises and Jasmine Enterprises?
Kelly's theory is applicable to all this and more.
"Fortune's Formula" by @WPoundstone is an excellent non-technical book that covers the Kelly Criterion in some detail.
amazon.com/Fortunes-Formu…
amazon.com/The-Dhandho-In…
amazon.com/Kelly-Capital-…
turtletrader.com/kelly.pdf
…godicityeconomics.files.wordpress.com/2018/06/ergodi…
/End
Turns out there’s actually some interest in the core mathematical theory behind the Kelly Criterion.
So, with a shout out to @borrowed_ideas who encouraged me to include this, here’s an appendix to the tweetstorm that gets into the math.
Instead of maximizing the wealth you expect to have at the end of each round, maximize the logarithm of this wealth.
At the start of a particular month, suppose our portfolio is worth $X. We divide this into two fractions: $f*X and $(1-f)*X.
We put $f*X in ALAD and keep $(1-f)*X in cash.
If we’re lucky, the ALAD part of our portfolio would have doubled. So the whole portfolio will be worth $f*X*2 + $(1-f)*X.
But if we’re unlucky, the ALAD part would have halved, leaving us with $f*X/2 + $(1-f)*X.
Lucky case: $X*(1+f)
Unlucky case: $X*(1-f/2)
Lucky case: log(X*(1+f))
Unlucky case: log(X*(1-f/2))
0.5*log(X*(1+f)) + 0.5*log(X*(1-f/2)),
which simplifies to:
log(X) + 0.5*log(1 + f/2 - f^2/2).
That’s the same as maximizing 1 + f/2 - f^2/2, which happens to be:
9/2 - 2*(f - 1/2)^2.
Maximizing this means minimizing (f - 1/2)^2.
And that means choosing f = 1/2.
So choosing f=1/2 means we put half the portfolio in ALAD stock.
The other half, (1-f), goes to cash.
And that’s how you do the math behind the Kelly Criterion.
But the key idea is the same: maximize the expectation of the logarithm of your wealth at every step.
/End