Thread by @jorgeluisaliaga

SOBRE GRAFICOS (lineal, exponencial): Este hilo lo debí hacer hace mucho, pero como esto lo había explicado en varias charlas que están en mi sitio web de COVID-19, pensé (mal) que ya no era necesario.
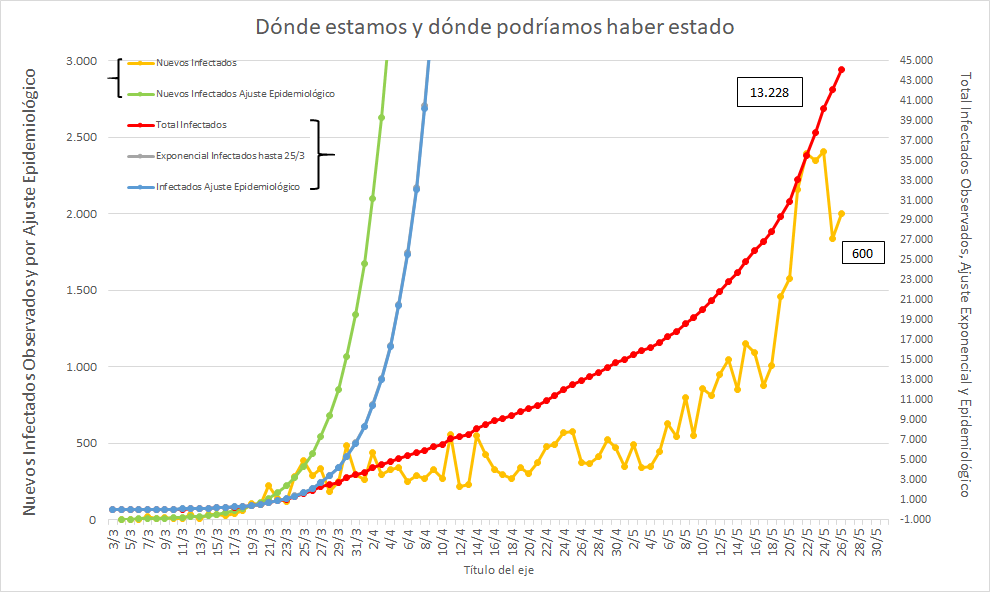
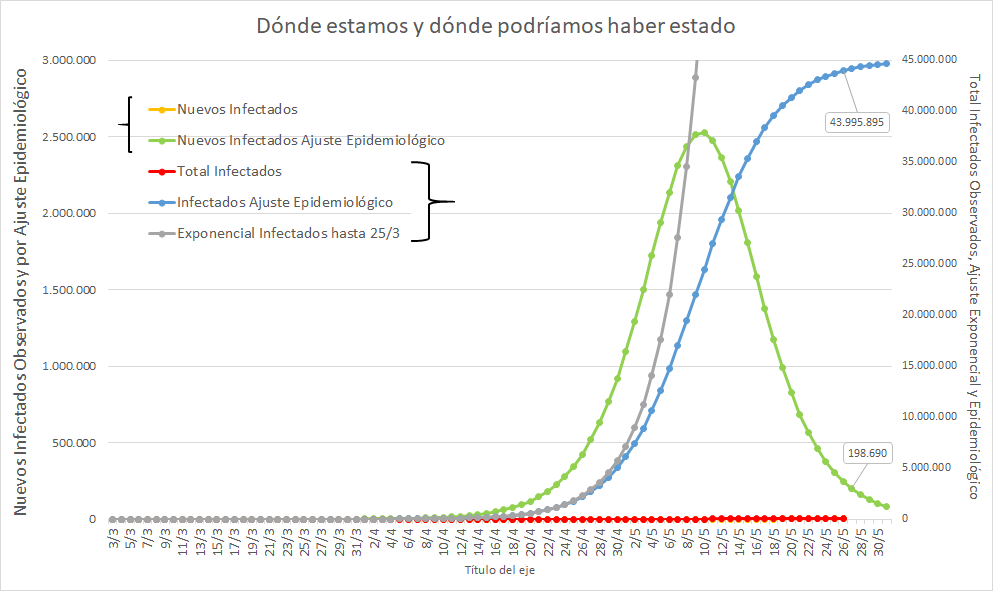
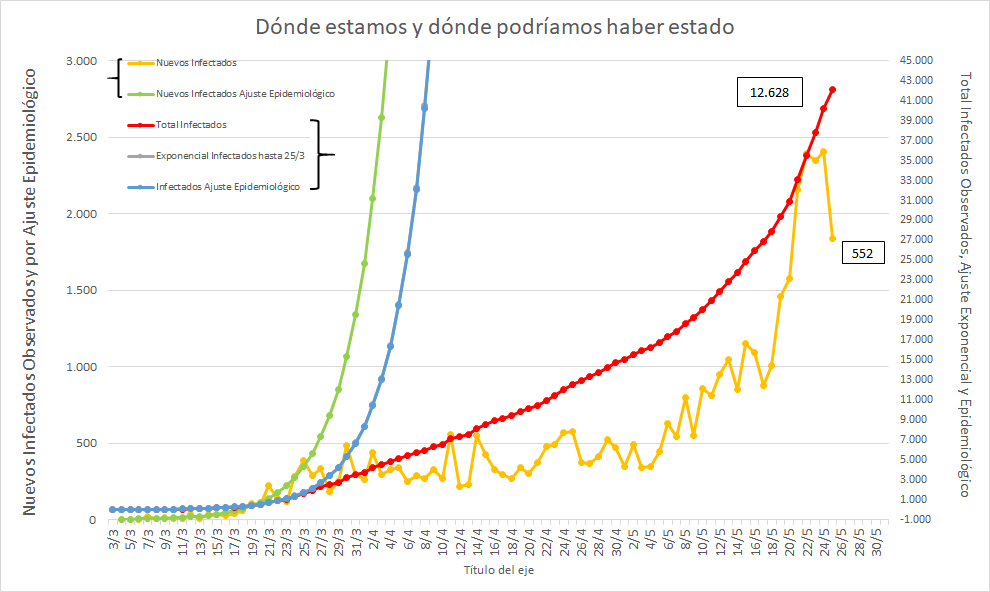
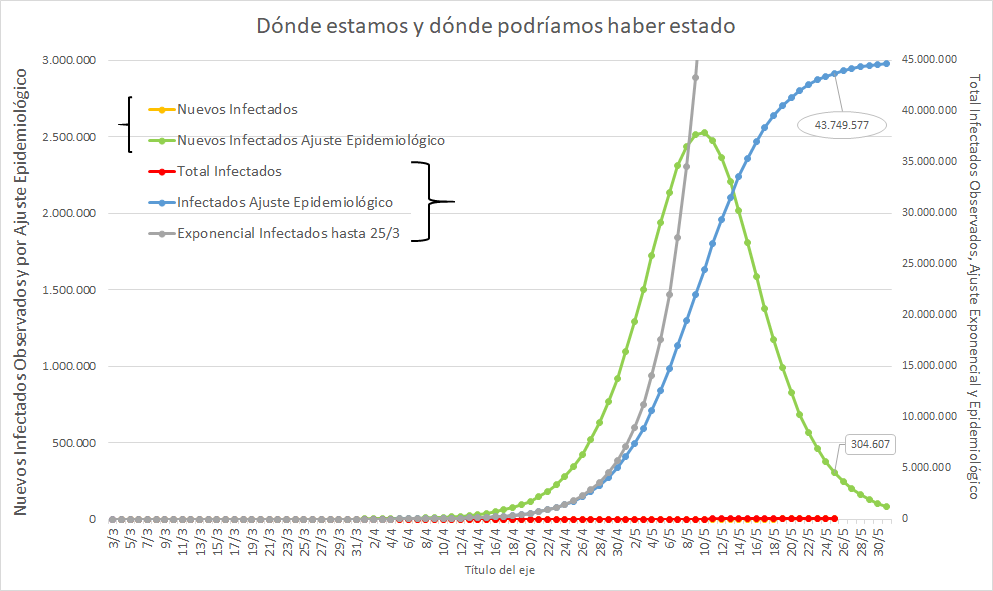
Sin embargo sigo viendo periodistas que se confunden.

1 /

Si uno grafica una función LINEAL (y = a * x), en una escala lineal en x e y, se ve así.
El valor de "a" indica la "velocidad" con que crece la función. Si "a" es más grande la función crece más rápido (llega a valores mayores de y para el mismo x).

2/

Ahora, acá muestro 3 funciones que NO son lineales. Las armé para que tengan valores iniciales y finales "similares". Son funciones DISTINTAS, las primeras dos son POTENCIAS, la tercera una EXPONENCIAL.

3 /

La linea "roja" muestra una recta que es "tangente" a la curva en un dado punto. Esa sería la "derivada" de la curva en ese punto. Como la curva no es lineal la derivada cambia de un punto a otro.

4 /

Y esa "derivada" da idea de la "velocidad" de cambio de la curva. En una curva lineal la velocidad es siempre la misma ("a"), porque justamente es una recta (su derivada, "a", es una constante).
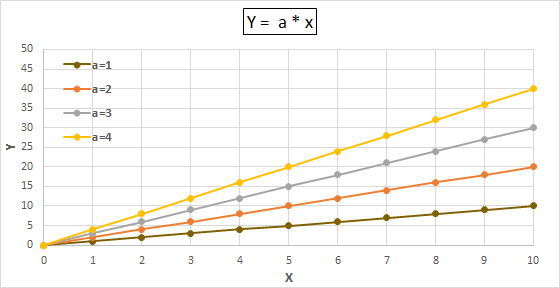
Eso no es así cuando la curva no es lineal.

5 /

Es MUY difícil decir "a ojo" cuál es la curva "cuadrática" (x^2), cúbica (x^3) o exponencial (e^x). Por eso no se hace "a ojo".
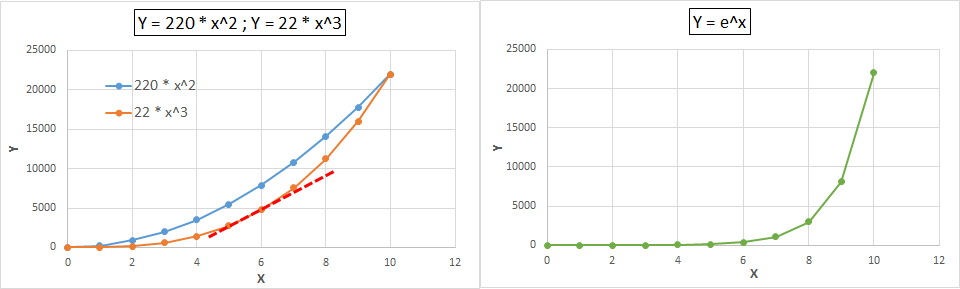
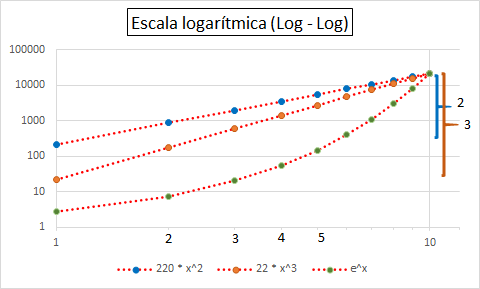
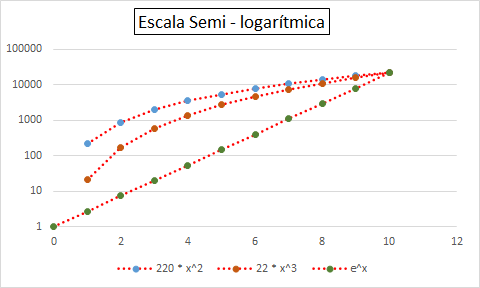
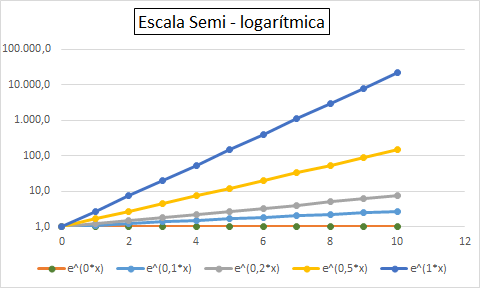
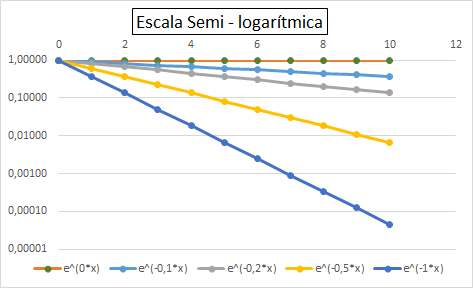
Se grafican las curvas usando distintas escalas, y se busca en qué escala la curva es una RECTA (es lo único que se ve "a ojo").

6 /

Acá muestro x^2, x^3 y e^x en escalas logarítmicas tanto en x como en y (log - log). En una escala logarítmica la distancia entre 1 y 10 es la misma que entre 10 y 100; 100 y 1000, ...
En este gráfico x^2 y x^3 (potencias) dan RECTAS

7 /

y la pendiente de la recta da la "potencia", como se muestra a la izquierda (2 y 3, respectivamente).
En cambio la "exponencial" NO da una recta, sino una curva.
Es decir, en log-log uno identifica "potencias", y obtiene el exponente, porque se ven como RECTAS

8 /

Ahora muestro las mismas funciones en escala lineal en x y logarítmica en y (semi-log).
En este gráfico la exponencial es una RECTA y las potencias son curvas.

9 /

Entonces, si uno tiene una función que no es lineal:
- graficás en log-log y da lineal, es potencia.
- graficás en semi-log y da lineal, es exponencial.

Ahora, si la función es y = e^(a*x), puedo calcular el valor de "a".

10/

Grafico la función y = e^(a*x) para a = 0; 0,1; 0,2; 0,5 y 1 en escala semi-log.
Todas son RECTAS, pero la "pendiente es distinta", porque la pendiente es "a".
(Ln(y) = a * x. Además, la derivada de y =e^(a*x), es y´ = a* e^(a*x) = a * y)

11 /

AHORA, vean en 10 "unidades de x" a qué valor llega y para cada valor de a:

a=0, y= 1
a=0,1 y= 2,7
a=0,2 y= 7,4
a=0,5 y= 148
a=1 y= 22.027

(cuando "a" = 0 los casos se mantienen constantes)

12 /

Puede parecer que la diferencia entre a=0 y a=0,1 es poca, pero al ser exponencial genera diferencias enormes en pocos cambios de x. Ni hablar si a=1.

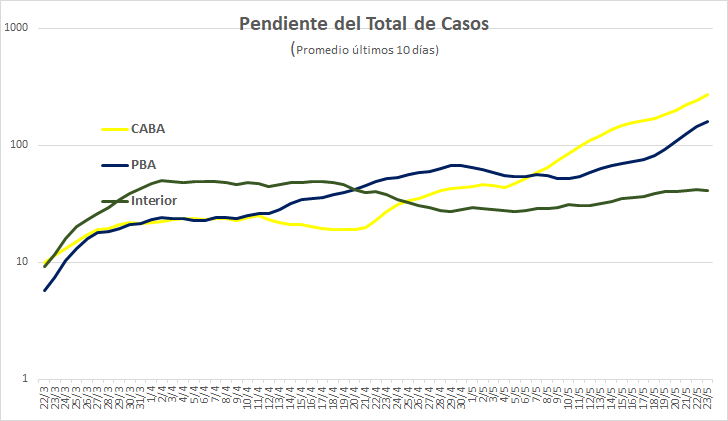
NO es cierto que si crece poco es "lineal" y si crece mucho es "exponencial". Y muchas crecen y no son exponencial

13 /

Eso depende de la forma de la curva, y del valor de "a".

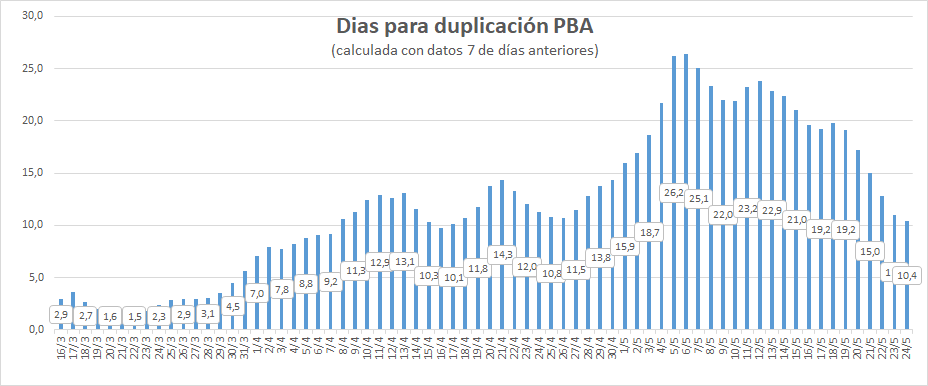
El número de días para duplicar decrece cuando crece "a".
El R (ritmo reproductivo), del que hablan los epidemiólogos, crece con "a".

14 /

Si "a" es menor que 0, los casos bajan (equivale a R menor que 1).
Cuando R es menor que 1 (a menor que cero) la epidemia se termina.

15 /

Visto esto, veámos como da la curva de Casos ordenados según fecha de síntoma en CABA (Los datos publicados por @msalnacion son de hace una semana)

16 /

El gráfico está en escala "semi-log". Desde el 10/4 es una recta (linea violeta).
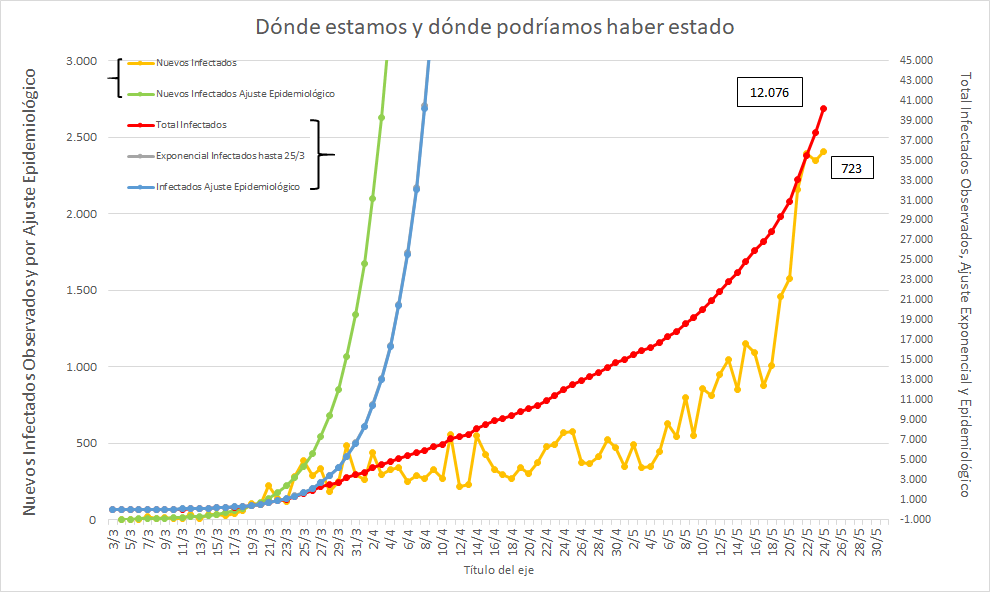
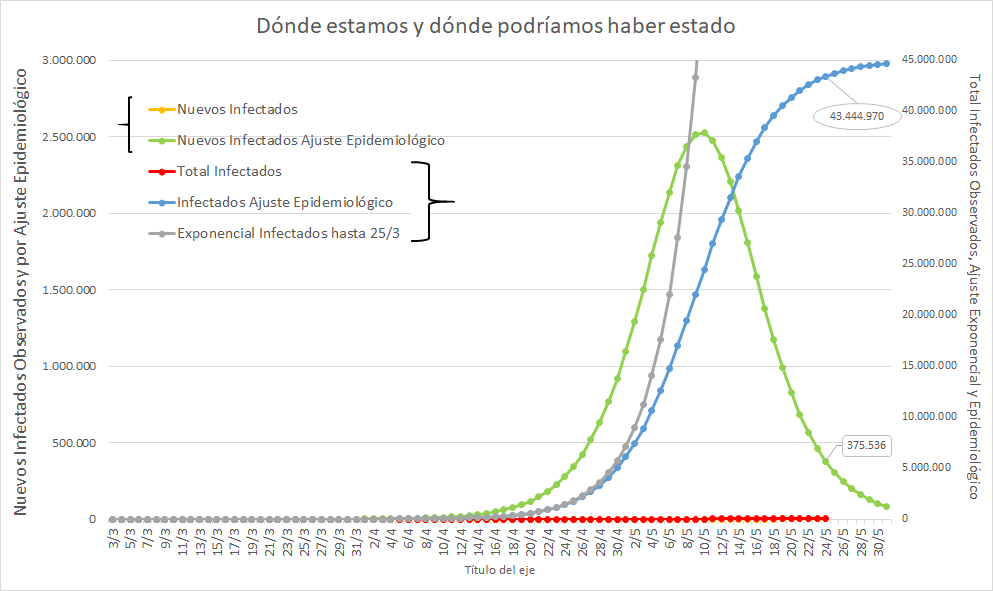
Uno puede calcular "a". La cantidad de días en los que se duplican los casos es Ln(2) / a. Si "a" es más grande, se duplica en menos días, es decir más rápido.

17 /

Hace 55 días que CABA crece exponencial, con una duplicación cada 11 días (aprox) hasta principios de mayo.

No tengo datos nuevos por fecha de síntoma, pero sí por fecha de confirmación (no es lo mejor, sino lo que hay):
En lo últimos días se acaleró CABA (y también PBA).

18 /

Esto se refleja en la cantidad de días de duplicación.

Si llegaron hasta acá, vieron de (12) que si a es mayor que 0 crece exponencial, más o menos rápido.
En ese réginen TODO satura, sólo cambia cuándo.

19 /

Y entonces voy al hilo de hoy de @rquiroga777 .
No importa el detalle de sus cuentas, porque a lo sumo cambian las cosas unos días, antes o después. El punto es que sólo NO satura si "a" es menor que 0. Y hace mucho que no lo es.

20 /

threadreaderapp.com/thread/1264751…

El ministro de Salud de CABA @FernanQuirosBA dijo hoy: "la evolución de la curva tomó una dinámica nueva, exponencial".
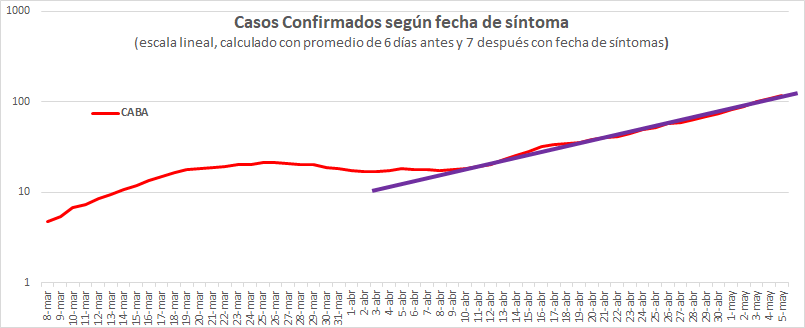
Como vimos, eso pasó hace 55 días. Primero por contagios de exceptuados, desde hace 40 también por Barrio Populares.

21 /

lanacion.com.ar/sociedad/coron…

Sobre cómo se generan picos, cada vez que uno quiera, pueden leer lo que escribí hace unos días. Si no se hizo lo necesario "a" es mayor que cero, cuando se hace, "a" es menor que cero ("pico").

Dista mucho de lo que dice el Ministro en esa nota.

22 /

jorgealiaga.com.ar/?p=2123

Lamento que no haya asesores científicos que puedan explicar esto de mejor forma.

Seguro periodistas científicas como @norabar @ValeriaRoman @NadiaLuna88 @FlorBallarino , .. lo contarían genial.

23 / 23 FIN

@threadreaderapp unroll