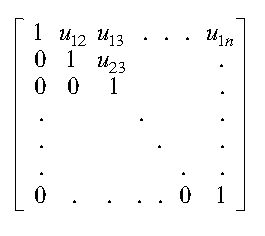Thread by @littmath

In celebration of reaching 3k followers, here's a thread on the Sylow theorems and algebraic geometry. I'll start by recalling the Sylow theorems, and then explain how they are in some cases manifestations of the geometry of certain algebraic varieties. 1/n

Let G be a finite group (say, the set of symmetries of some object) and p a prime. If the size |G| of G is p^k*m, where m is not divisible by p, we call a subgroup of G a *p-Sylow subgroup* if it has size p^k.

The first Sylow theorem says p-Sylow subgroups always exist. 2/n

That is, there is always a subgroup of G of order p^k, where k is as big as can be (since the size of a subgroup always divides the size of the group). 3/n

For example, let G be the set of symmetries of a regular tetrahedron. this has size 4!=24=2^3*3, so we want to construct a subgroup of size 3 and a subgroup of size 2^3=8. 4/n

Making the four 3-Sylow subgroups is easy; they're just given by rotation 0, 120, or 240 degrees along the axis between a vertex and the center of the opposite face (that is, the dotted blue line in the picture below). 5/n

The 2-Sylow subgroups, of order 8, are harder to see. Divide the six edges of the tetrahedron into three sets of two disjoint edges each (labeled {u,U}, {v, V}, {w,W} in the picture). Then fix one of these pairs, say (v,V). The set of symmetries preserving {v,V} is a 2-Sylow. 6/n

The second Sylow theorem says that any two p-Sylow subgroups are conjugate to one another. In our example, a 3-Sylow is determined by an axis of rotation. So if a symmetry takes one axis of rotation to another, it conjugates the corresponding 3-Sylows into one another. 7/n

A 2-Sylow is determined by a pair of disjoint edges of the tetrahedron; again, a symmetry sending one such pair into another conjugates the corresponding 2-Sylows into one another. 8/n

Finally, the third Sylow theorem says that the *number* of p-Sylow subgroups is always 1 modulo p. For example, their are four 3-Sylow subgroups above (as there are four possible axes of rotation) and three 2-Sylow subgroups (as there are three pairs of disjoint edges). 9/n

OK, now I want to talk about how this is related to algebraic geometry. Let p be a prime, let F_p be the field with p elements, and let G=GL_n(F_p) be the group of n x n invertible matrices with coefficients in F_p. 10/n

This is the set of automorphisms of an n-dimensional F_p-vector space V=F_p^n.

What is the size of this group? 11/n

Well, the first column of an invertible matrix can be any non-zero vector, so there are p^n-1 choices. The second can be any vector not in the span of the first, so there are p^n-p choices. The third can be anything not in the span of the first two, so p^n-p^2 choices. 12/n

Continuing in this manner, we see that the size of GL_n(F_p) is

(p^n-1)(p^n-p)(p^n-p^2)...(p^n-p^{n-1}).

The biggest power of p dividing this number is

p^{1+2+...+(n-2)+(n-1)}=p^{n(n-1)/2},

so a p-Sylow of G should have size p^{n(n-1}/2}. 13/n

Let's make such a subgroup! Take upper-triangular matrices with 1's on the diagonal. Such matrices are always invertible, so we can fill in the upper right triangle however we want. There are n(n-1)/2 entries, and we have p choices for each, so this is indeed a p-Sylow. 14/n

Now the second Sylow theorems tells us that any other p-Sylow is conjugate to this one, and the third tells us that the number of such p-Sylows is equal to 1 mod p.

But what does this mean geometrically? 15/n

Suppose you're given a *full flag* of your vector space V. That is, a sequence of subspace V_1 ⊂ V_2 ⊂ V_3 ⊂ ... ⊂ V_n=V, where V_i is i-dimensional. Consider the set of matrices which preserve this flag and act trivially on V_i/V_{i-1} for each i. This is a p-Sylow! 16/n

Indeed, our original p-Sylow is the case where each V_i is spanned by the first i standard basis vectors. 17/n

Given an arbitrary full flag, choosing a basis where V_i is spanned by the first i basis vectors shows that any full flag can be sent to any other by some element of G; hence the same element of G conjugates the corresponding p-Sylows into one another. 18/n

Finally, let's count full flags, and hence p-Sylows. How many choices are there for V_1? Well, if we choose a vector spanning V_1, there are p^n-1 choices. But rescaling our vector gives the same V_1, so there are really

(p^n-1)/(p-1) = 1+p+...+p^{n-1}

choices. 19/n

Now given any full flag V_1 ⊂ V_2 ⊂ V_3 ⊂ ..., quotienting by V_1 gives a full flag of an (n-1)-dimensional vector space. So induction tells us that the number of full flags is

(p^n-1)(p^{n-1}-1)...(p^2-1)/(p-1)^{n-1}=
(1+p+...+p^{n-1})(1+p+...+p^{n-2})...(1+p).

20/n

And this is indeed 1 modulo p, as claimed. 21/n

OK, but I promised you some geometry. So let's find a version of the Sylow theorems over the complex numbers! Set G=GL_n(C), the set of n x n invertible matrices with complex coefficients. This is the set of automorphisms of the vector space V=C^n. 22/n

This is an infinite group, so we can't look for p-Sylows; instead, taking a page out of our GL_n(F_p) example, we'll look for subgroups which stabilize a *full flag* V_1 ⊂ V_2 ⊂ V_3 ⊂ ... ⊂ V_n=V and act trivially on V_i/V_{i-1}. 23/n

These subgroups have a name and an intrinsic description; they're called "maximal unipotent subgroups." 24/n

The same argument as before -- that GL_n(C) acts transitively on the set of full flags -- tells us that any two such subgroups are conjugate to one another. But what's the analogue of the third Sylow theorem? 25/n

Well, there are infinitely many maximal unipotent subgroups, so we can't count them. But instead, we can analyze the geometry of the *space* of maximal unipotent subgroups, or equivalently the space of full flags. 26/n

This space has a name -- it's called the flag variety, and I'll denote it by FL_n. The map sending a full flag V_1 ⊂ V_2 ⊂ V_3 ⊂ ... ⊂ V_n=V to V_1 is a map from FL_n --> P^{n-1}, where P^{n-1} is the space of one-dimensional subspaces of V. 27/n

And just like before, the fibers of this map are full flags on V/V_1, and so they're isomorphic to Fl_{n-1}.

Now we can write P^{n-1}=pt ∪ C^1 ∪ C^2 ∪ ... ∪ C^{n-1}, so a (non-trivial!) inductive argument shows that Fl_n is a union of copies of C^m. 28/n

How many copies of C^m show up? Well the exact same argument from before shows it's the coefficient of L^m in the polynomial

(1+L+...+L^{n-1})(1+L+...+L^{n-2})...(1+L).

29/n

This polynomial is 1 modulo L! And that's a geometric analogue of the third Sylow theorem (for GL_n).

Doing this argument in algebraic geometry (rather than complex analytically) implies the third Sylow theorem for GL_n(F_p) for all p. 30/n

In fact the same kind of argument works for general "split reductive groups" (think Sp_{2n}, SO_n, PGL_n, etc.) -- the associated "generalized flag varieties" always have cell decompositions like this. 31/n

And the existence of these cell decompositions always implies the corresponding Sylow theorems for the analogues of these groups over finite fields. 32/n

But one can do more! For example, instead of considering "maximal unipotent subgroups," you can consider other types of subgroups. For example, all tori in GL_n(C) are conjugate to each other (and to the group of diagonal matrices). 33/n

For example the space of tori in GL_2(C) has fundamental group Z/2Z; it has torsion cohomology away from degree zero. I claim that this is analogous to the fact that there are p^2 tori in GL_n(F_p). 34/n

And there's lots more one can do, by e.g. considering block upper triangular matrices or other types of groups, but I'll end here! 35/35.

Ah sorry that “n” in GL_n should be a 2!

BTW, it's mentioning that I started thinking about this b/c of some very interesting conversations with/questions from @AShmakovMath!