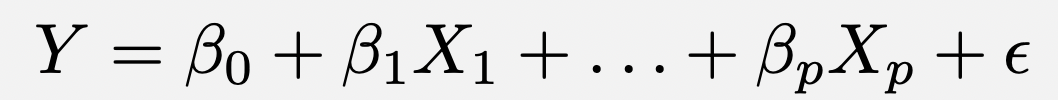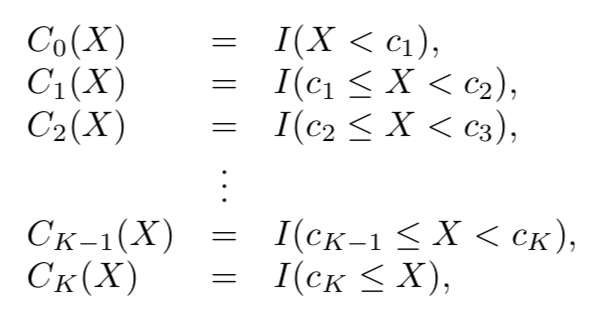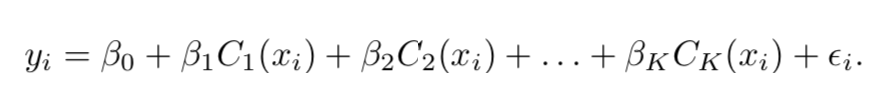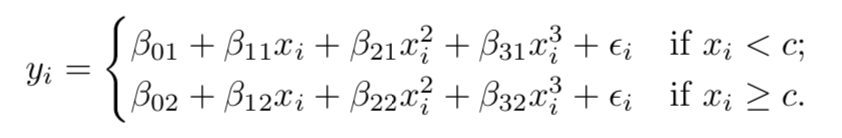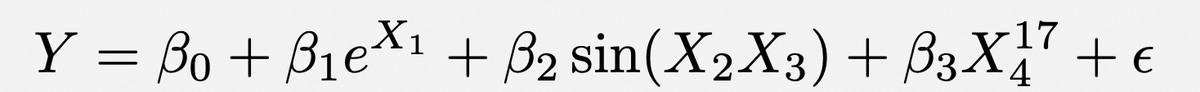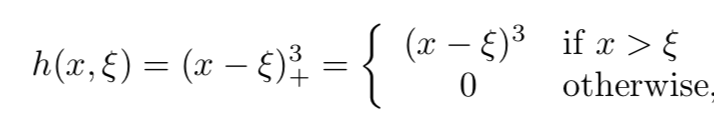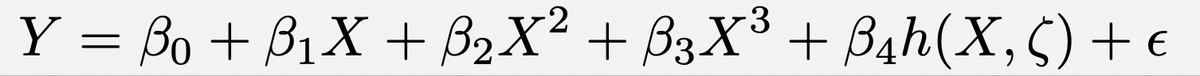Thread by @WomenInStat

Today, we’re going to play a game I’m calling “IT’S JUST A LINEAR MODEL” (IJALM).

It works like this: I name a model for a quantitative response Y, and then you guess whether or not IJALM.

1/

I’ll go first:

Y= \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_p X_p + \epsilon

You guessed it …. IJALM!

2/

How about the lasso? Ridge regression?

IJALM but you’re not fitting it using least squares — it’s penalized/regularized least squares instead.

3/

How about forward or backward stepwise regression regression?

IJALM using a subset of the predictors. We fit the linear model using least squares on a subset of the predictors, though of course this isn’t the same is if we had performed least squares on ALL the predictors.

4/

How about a piecewise constant model? Like this one?

You guessed it… IJALM, using basis functions that are piecewise constant. Typically fit with least squares.

5/

What if it’s piecewise cubic?

Yes, IJALM, but now the basis functions are piecewise cubic. Fit with least squares.

6/

Now, what if I predict Y using very complicated functions of my features, like e^{X_1}, \sin(X_2 X_3), and X_4^{17}?

Can’t fool me!!! IJALM! It’s linear in transformations of the features, e^{X_1}, \sin (X_2 X_3), and X_4^17. Can fit with least squares.

7/

OK, how about a B-spline (or regression spline)? [Remember: a kth-order B-spline is a piecewise kth-order polynomial w/derivatives that are cont. up to order k-1.]

You guessed it: IJALM. The basis functions look wacky, but nonetheless, IJALM. Fit using least squares.

8/

Alright, on to the good stuff.

How about a regression tree? That is fundamentally non-linear, right?

Well, sort of . . . but no. IJALM w/ adaptive choice of predictors (predictors are indicator variables corresponding to a region of tree). Fit w/least squares.

9/

OK, this is getting old. How about principal components regression? Non-linear, right?

Well, no. The model is linear in the PCs, which are linear in the features, so, IJALM. Fit w/least squares.

Partial least squares? IJALM, for the same reason. Fit using least squares.

10/

How about deep learning? Super non-linear, right?

Well, as a function of some non-linear activations, it's IJALM.

You can put lipstick on a linear model, but it’s still a linear model.

Fit it w/least squares … w/ bells & whistles like dropout, SGD, & regularization.

11/

So to sum it all up:

No you didn't fit a "super complicated non-linear model”. I bet you all my winnings from this round of IJALM it was actually JALM.

Perhaps not linear in the original features, and perhaps fit using a variant of least squares. But, IJALM nonetheless.

12/

Linear models.

They might not be what your data thinks it wants, but they’re what your data needs, and they’re almost certainly what your data is going to get.

13/

Thanks for playing!!!

Stay tuned for my next installment: IT’S JUST LOGISTIC REGRESSION (IJLR), which is literally just this same exact thread but now Y is a binary response.

14/14