Thread by @daniela_witten

The Bias-Variance Trade-Off & "DOUBLE DESCENT" 🧵

Remember the bias-variance trade-off? It says that models perform well for an "intermediate level of flexibility". You've seen the picture of the U-shape test error curve.

We try to hit the "sweet spot" of flexibility.

1/🧵

This U-shape comes from the fact that

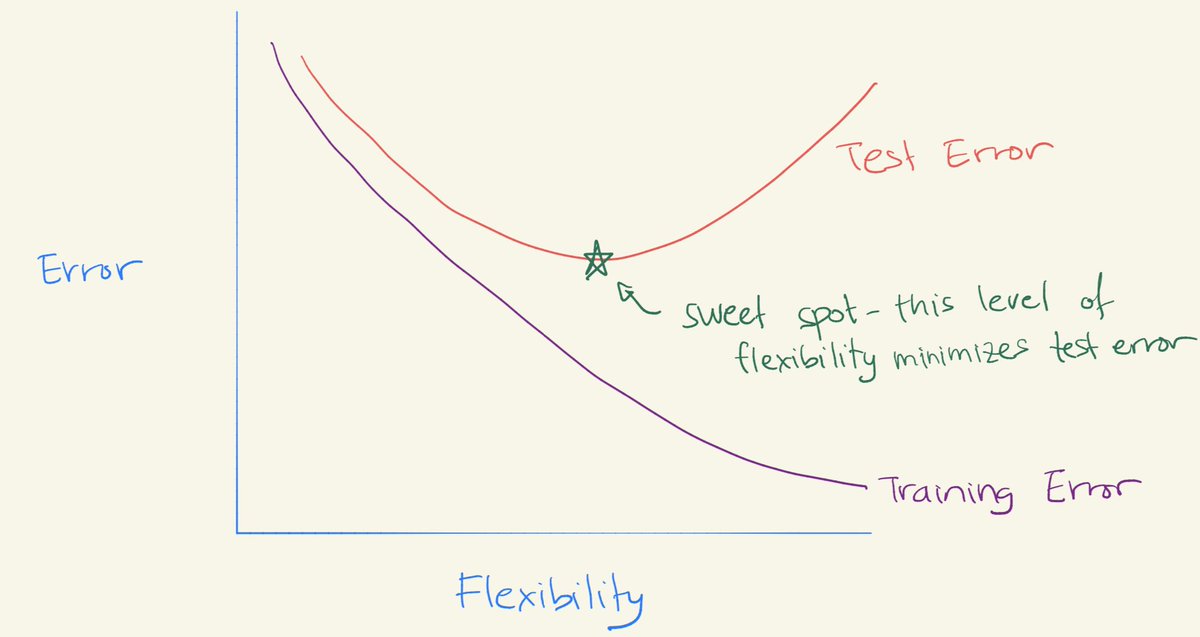
Exp. Pred. Error = Irreducible Error + Bias^2 + Var

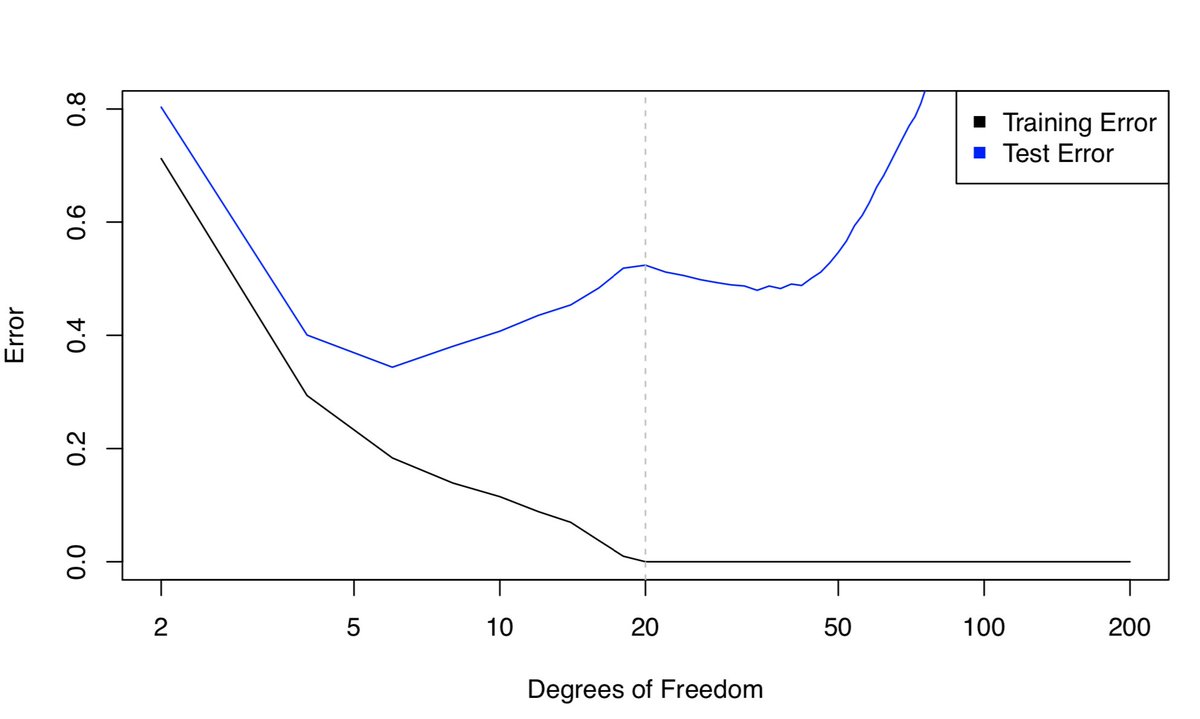
As flexibility increases, (squared) bias decreases & variance increases. The "sweet spot" requires trading off bias and variance -- i.e. a model with intermediate level of flexibility.

2/

In the past few yrs, (and particularly in the context of deep learning) ppl have noticed "double descent" -- when you continue to fit increasingly flexible models that interpolate the training data, then the test error can start to DECREASE again!!

Check it out: 
3/

This seems to come up in particular in the context of deep learning (though, as we'll see, it happens elsewhere too).

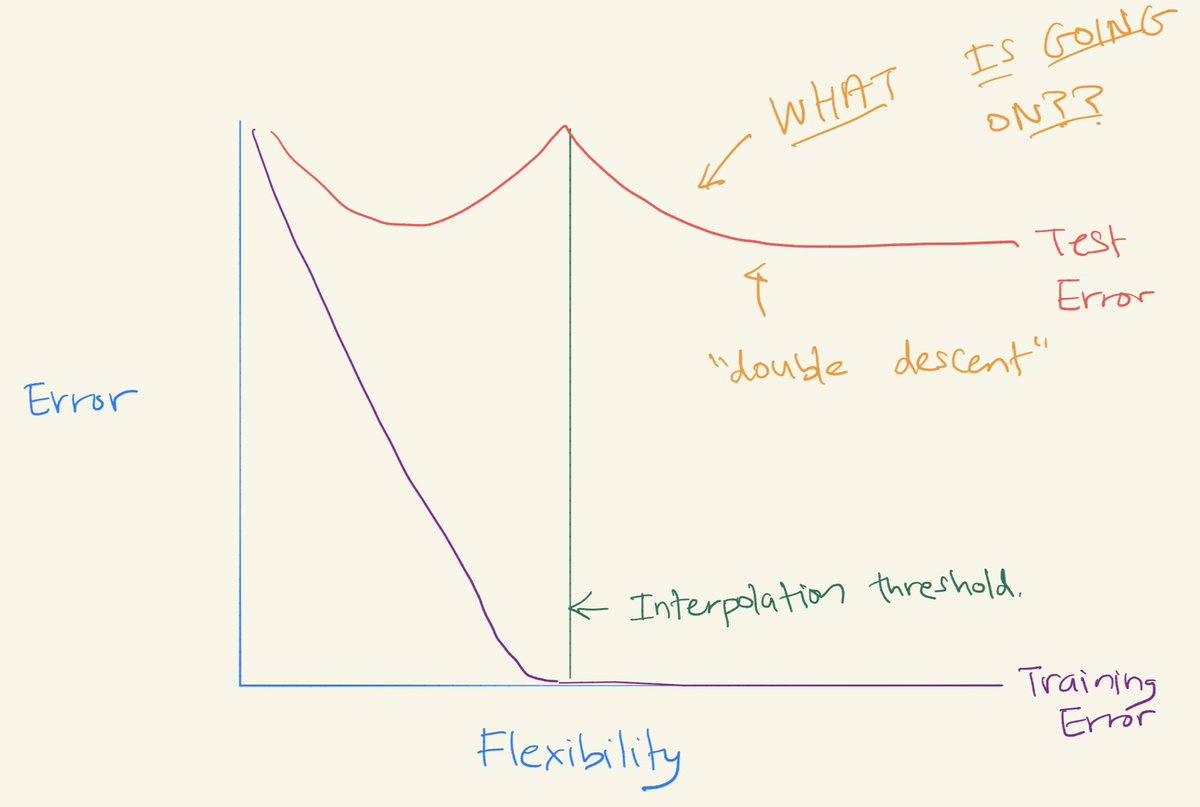
What the heck is going on? Does the bias-variance trade-off NOT HOLD? Are the textbooks all wrong?!?!?!

Or is deep learning *magic*?

4/

OK everyone, hold onto your hats.

I promise, the bias-variance trade-off is OK!

To understand double descent, let's check out a simple example that has nothing to do with deep learning: natural cubic splines.

5/

What's a spline? Basically, it's a way to fit the model Y=f(X)+epsilon, with f non-parametric, using very smooth piecewise polynomials.

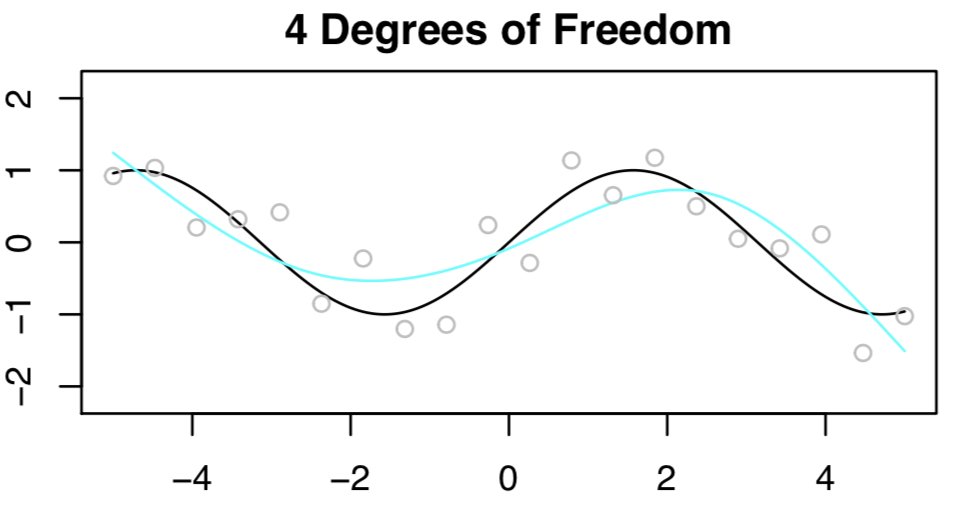
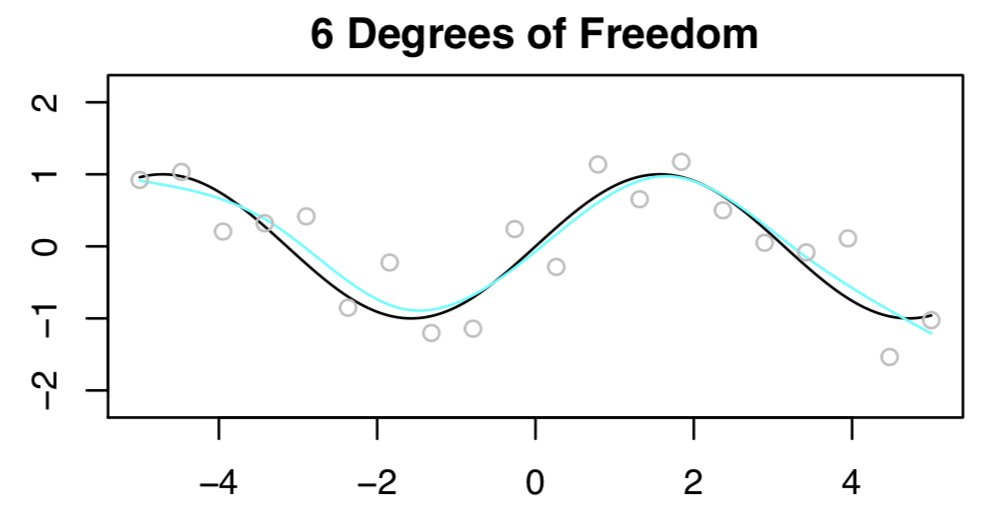
To fit a spline, we construct some basis functions and then fit the response Y to the basis functions via least squares.

6/

The number of basis functions we use is the number of *degrees of freedom* of the spline.

The basis functions more or less look like this, but the details really aren't that important.

7/

OK, so, suppose we have n=20 (X,Y) pairs, and we want to estimate f(X) in Y=f(X)+epsilon (here f(X)=sin(X)) using a spline.

First we fit a spline w/ 4 DF. The n=20 observations are in gray, true function f(x) is in black, and the fitted function is in light blue. Not bad!

8/

Now let's try again, this time with 6 degrees of freedom. Bam -- looks awesome!! 

9/

Now what if we use 20 degrees of freedom? Ummm... this is a bad idea... because we have n=20 observations and to fit a spline with 20 DF I need to run least squares with 20 features!! We'll get ZERO training error (i.e. interpolate the training set) and bad test error!

10/

And you can see it from the figure.... bad results... just as the bias-variance trade-off predicts. All's well in the world.

11/

Now put on your seatbelt because we're to fit a spline with 36 DF.

You heard me right: least squares with n=20 and p=36. WHAT THE WHAT?!!

12/

W/ p>n the LS solution isn't even unique!

To select among the infinite number of solutions, I choose the "minimum" norm fit: the one with the smallest sum of squared coefficients. [Easy to compute using everybody's favorite matrix decomp, the SVD.]

https://twitter.com/WomenInStat/status/1285610321747611653?s=20

13/

The result will be HORRIBLE, because p>n, right??

Right??!!!!!!

Here's what we get:

14/

Hmmm... not as bad as we expected... let's compare the results with 20 DF to 36 DF....

what is going on??? Shouldn't the fit with 36 DF look WORSE than the one with 20 DF? If anything, it looks a little BETTER!!

15/

We can take a peek at the training and test error:

WHAT THE HECK IS HAPPENING?!??!  Why did the test error (briefly) DECREASE when p>n? Isn't that literally THE OPPOSITE of what the bias-variance trade-off says should happen?

Should we burn our copies of ISL?!

16/

Calm down!! This actually makes sense.

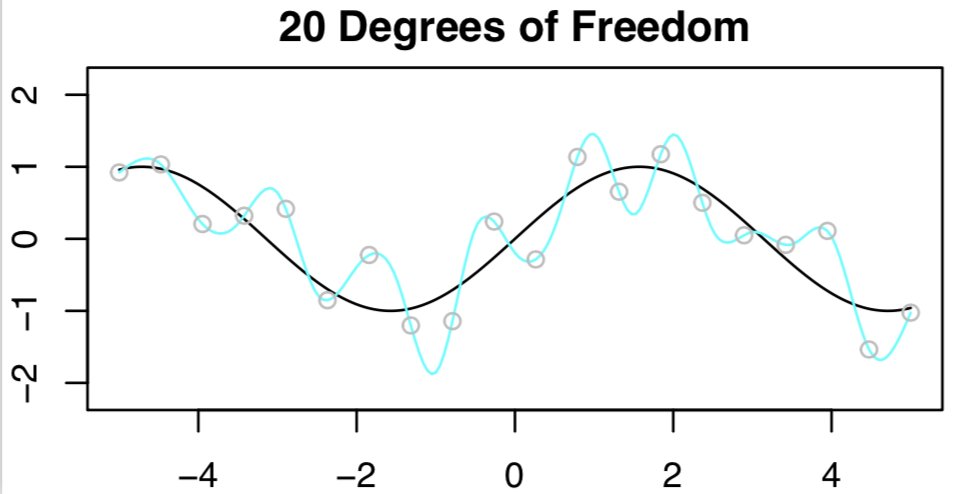
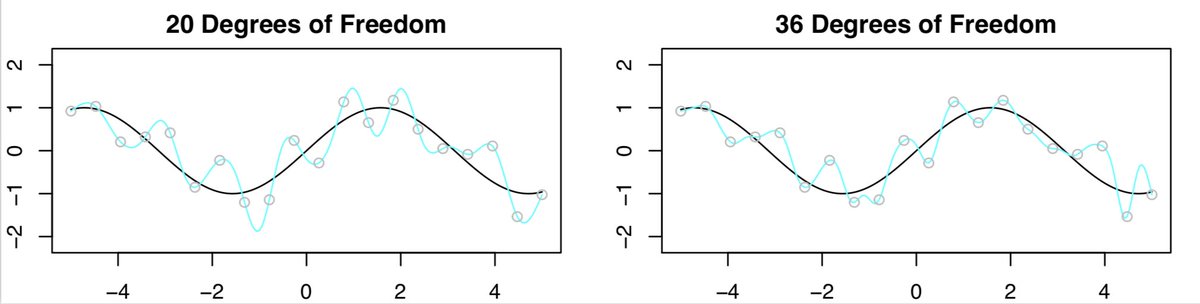
The key point is with 20 DF, n=p, and there's exactly ONE least squares fit that has zero training error. And that fit happens to have oodles of wiggles.....

17/

.... but as we increase the DF so that p>n, there are TONS of interpolating least squares fits.

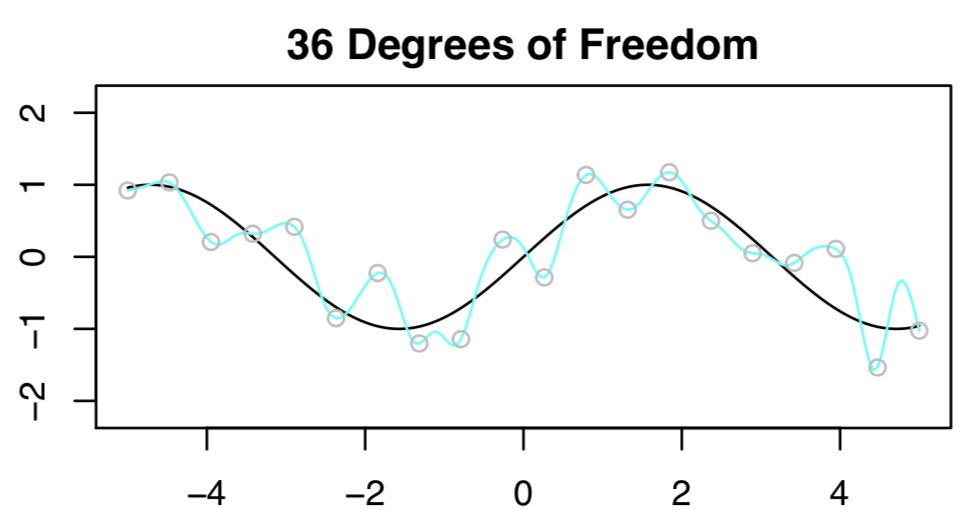
The MINIMUM NORM least squares fit is the "least wiggly" of those zillions of fits. And the "least wiggly" among them is even less wiggly than the fit when p=n !!!

18/

So, "double descent" is happening b/c DF isn't really the right quantity for the the x-axis: like, the fact that we are choosing the minimum norm least squares fit actually means that the spline with 36 DF is **less** flexible than the spline with 20 DF.

Crazy, huh?

19/

Now... what if had used a ridge penalty when fitting the spline (instead of least squares)?

Well then we wouldn't have interpolated training set, we wouldn't have seen double descent, AND we would have gotten better test error (for the right value of the tuning parameter!)

20/

How does this relate to deep learning?

When we use (stochastic) gradient descent to fit a neural net, we are actually picking out the minimum norm solution!!

So the spline example is a pretty good analogy for what is happening when we see double descent for neural nets.

21/

So, what's the point?

✅ double descent is a real thing that happens
✅ it is not magic 🚫
✅ it is understandable through the lens of stat ML and the bias-variance trade-off.

Actually, the B/V T/O helps us understand *why* DD is happening!

No magic ... just statistics 

22/

But then again ... statistics is magical!! 💫💫💫🪄

Thanks to my co-authors @robtibshirani @HastieTrevor and Gareth James for discussions leading to some of the ideas in this thread

24/24