1/
Get a cup of coffee.
In this thread, I'll help you understand geometric sequences.
Geometric sequences are the basis for *so* many financial calculations -- from DCFs to mortgages.
And the math behind them is not very complicated. So I think it makes sense to master it.
Get a cup of coffee.
In this thread, I'll help you understand geometric sequences.
Geometric sequences are the basis for *so* many financial calculations -- from DCFs to mortgages.
And the math behind them is not very complicated. So I think it makes sense to master it.
2/
First things first. What is a geometric sequence?
In simple terms, it's just a list of numbers.
But not just any numbers.
No, these numbers have a very special property: they grow (or shrink) *exponentially*.
First things first. What is a geometric sequence?
In simple terms, it's just a list of numbers.
But not just any numbers.
No, these numbers have a very special property: they grow (or shrink) *exponentially*.
3/
Here's an example.
Suppose your 2020 salary is $100K. And you get a 5% raise every year.
So, in 2021, your salary will be $100K * 1.05 = $105K.
And in 2022, your salary will be $105K * 1.05 = $110.25K.
And so on.
Here's an example.
Suppose your 2020 salary is $100K. And you get a 5% raise every year.
So, in 2021, your salary will be $100K * 1.05 = $105K.
And in 2022, your salary will be $105K * 1.05 = $110.25K.
And so on.
4/
These salary numbers -- $100K, $105K, $110.25K, etc. -- are growing *exponentially*.
In other words, they form a geometric sequence.
Here's a graph of this sequence:
These salary numbers -- $100K, $105K, $110.25K, etc. -- are growing *exponentially*.
In other words, they form a geometric sequence.
Here's a graph of this sequence:

5/
But suppose your annual salary increments were a fixed *dollar amount* (say, $5K) instead of a fixed *percentage* (like 5%).
In this case, your "salary sequence" will be: $100K, $105K, $110K, $115K, ...
But suppose your annual salary increments were a fixed *dollar amount* (say, $5K) instead of a fixed *percentage* (like 5%).
In this case, your "salary sequence" will be: $100K, $105K, $110K, $115K, ...
6/
These salary numbers are growing too.
But they're growing only *linearly*. Not *exponentially*.
So these numbers don't form a geometric sequence.
These salary numbers are growing too.
But they're growing only *linearly*. Not *exponentially*.
So these numbers don't form a geometric sequence.
7/
The math behind geometric sequences is super simple.
A geometric sequence has just 2 parameters:
1. The first number (denoted "a"), and
2. The exponential growth rate (denoted "r").
If you know these 2 parameters, you can construct the entire sequence.
The math behind geometric sequences is super simple.
A geometric sequence has just 2 parameters:
1. The first number (denoted "a"), and
2. The exponential growth rate (denoted "r").
If you know these 2 parameters, you can construct the entire sequence.
8/
So, knowing "a" and "r", how exactly do you construct the entire sequence?
It's simple. You just have to do some multiplications.
The first number in the sequence is: a.
The second number is: a*r.
The third number is: a*r*r.
The fourth number is: a*r*r*r.
And so on.
So, knowing "a" and "r", how exactly do you construct the entire sequence?
It's simple. You just have to do some multiplications.
The first number in the sequence is: a.
The second number is: a*r.
The third number is: a*r*r.
The fourth number is: a*r*r*r.
And so on.
9/
Let's try to connect this with your exponentially growing salary.
Remember: you start at $100K in 2020, and you get a 5% raise every year. So:
Your 2020 salary is: $100K.
Your 2021 salary is: $100K * 1.05.
Your 2022 salary is: $100K * 1.05 * 1.05.
And so on.
Let's try to connect this with your exponentially growing salary.
Remember: you start at $100K in 2020, and you get a 5% raise every year. So:
Your 2020 salary is: $100K.
Your 2021 salary is: $100K * 1.05.
Your 2022 salary is: $100K * 1.05 * 1.05.
And so on.
10/
Just look at the last 2 tweets.
You don't need a whole lot of pattern recognition to see that your salary sequence is simply a geometric sequence with a = $100K and r = 1.05.
Just look at the last 2 tweets.
You don't need a whole lot of pattern recognition to see that your salary sequence is simply a geometric sequence with a = $100K and r = 1.05.
11/
This is why geometric sequences arise in so many financial calculations.
Whenever you have money that's compounding steadily -- whether it's salaries, dividends, revenues, earnings, or free cash flows -- it's a good bet that there's a geometric sequence in there somewhere.
This is why geometric sequences arise in so many financial calculations.
Whenever you have money that's compounding steadily -- whether it's salaries, dividends, revenues, earnings, or free cash flows -- it's a good bet that there's a geometric sequence in there somewhere.
12/
OK. So what useful things can we learn about geometric sequences, that'll help us with our financial calculations?
There are 2 key formulas:
1. Formula for the n'th number, and
2. Formula for the sum of the first n numbers.
OK. So what useful things can we learn about geometric sequences, that'll help us with our financial calculations?
There are 2 key formulas:
1. Formula for the n'th number, and
2. Formula for the sum of the first n numbers.
13/
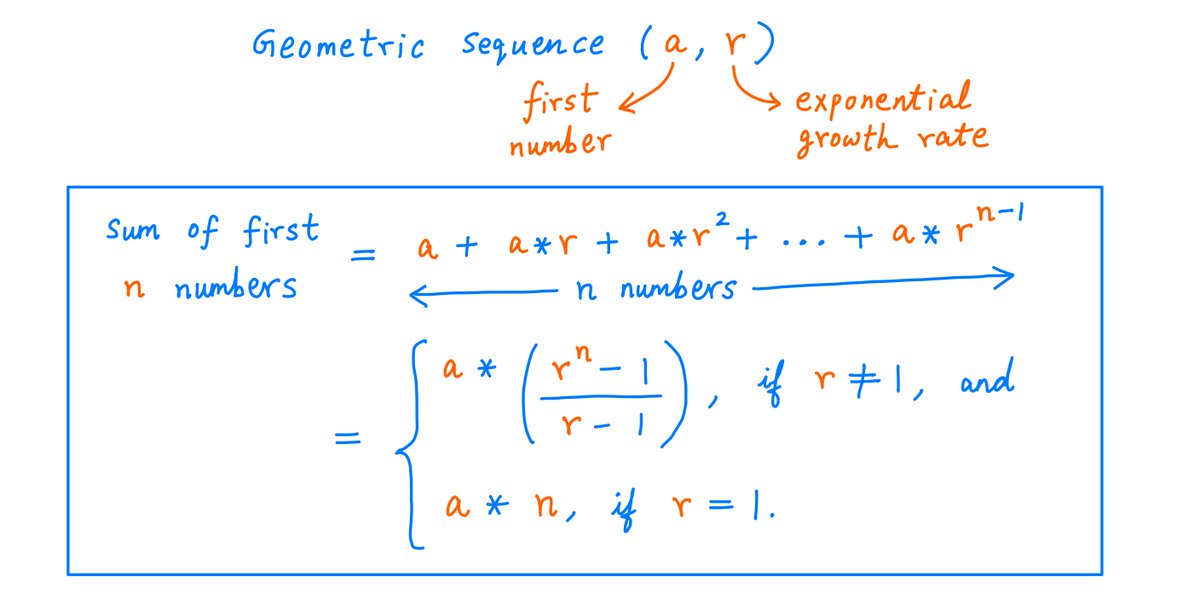
Formula for the n'th number of a geometric sequence.
This is a pretty simple formula. It's almost self-evident. Pics:

Formula for the n'th number of a geometric sequence.
This is a pretty simple formula. It's almost self-evident. Pics:


14/
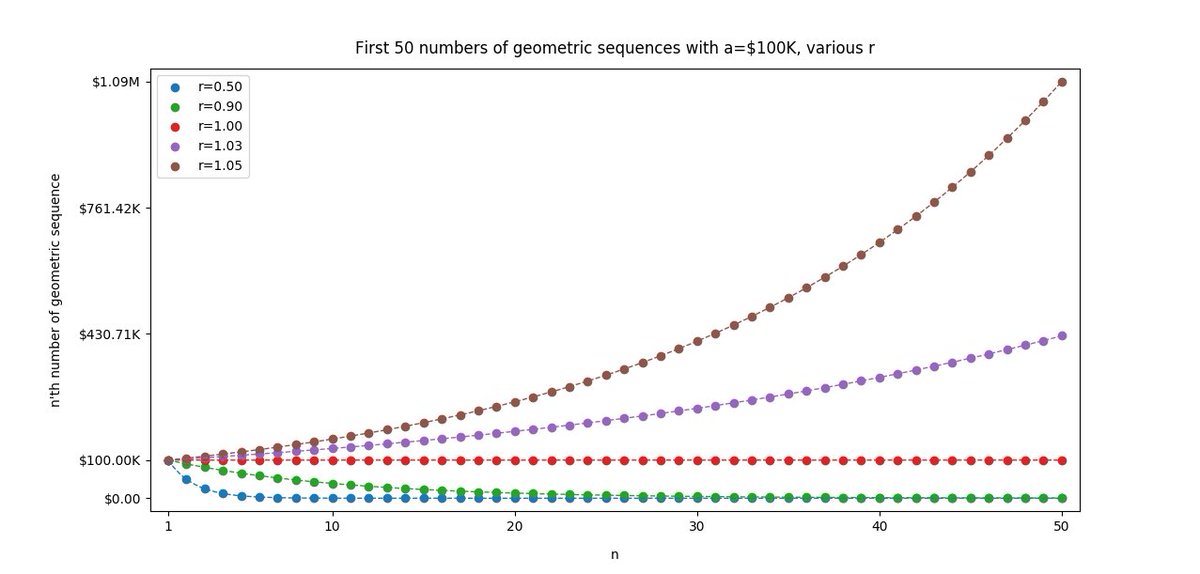
By applying the formula above to various "n" and "r" values (holding "a" constant at $100K), you can get a qualitative feel for geometric sequences.
For example, you can tell from the picture below that if r > 1, the numbers in the sequence will grow exponentially.
By applying the formula above to various "n" and "r" values (holding "a" constant at $100K), you can get a qualitative feel for geometric sequences.
For example, you can tell from the picture below that if r > 1, the numbers in the sequence will grow exponentially.
15/
But if 0 < r < 1, the numbers in the sequence will *shrink* exponentially -- and get close to 0 pretty quickly.
Finally, if r is exactly equal to 1, the numbers will neither grow nor shrink. They will remain constant at "a", no matter how large you make "n".
But if 0 < r < 1, the numbers in the sequence will *shrink* exponentially -- and get close to 0 pretty quickly.
Finally, if r is exactly equal to 1, the numbers will neither grow nor shrink. They will remain constant at "a", no matter how large you make "n".
17/
I've found the formula above extraordinarily useful.
It simplifies so many different kinds of financial calculations.
I think this is the third most useful formula in all of finance -- after the compound interest and present value formulas.
I've found the formula above extraordinarily useful.
It simplifies so many different kinds of financial calculations.
I think this is the third most useful formula in all of finance -- after the compound interest and present value formulas.
18/
Let me demonstrate.
Suppose you start with a $100K salary in 2020, and get a 5% raise each year.
You save 25% of your salary each year.
You invest these savings in a basket of stocks, which goes up 7% each year.
How much money will you have at the end of 2050?
Let me demonstrate.
Suppose you start with a $100K salary in 2020, and get a 5% raise each year.
You save 25% of your salary each year.
You invest these savings in a basket of stocks, which goes up 7% each year.
How much money will you have at the end of 2050?
19/
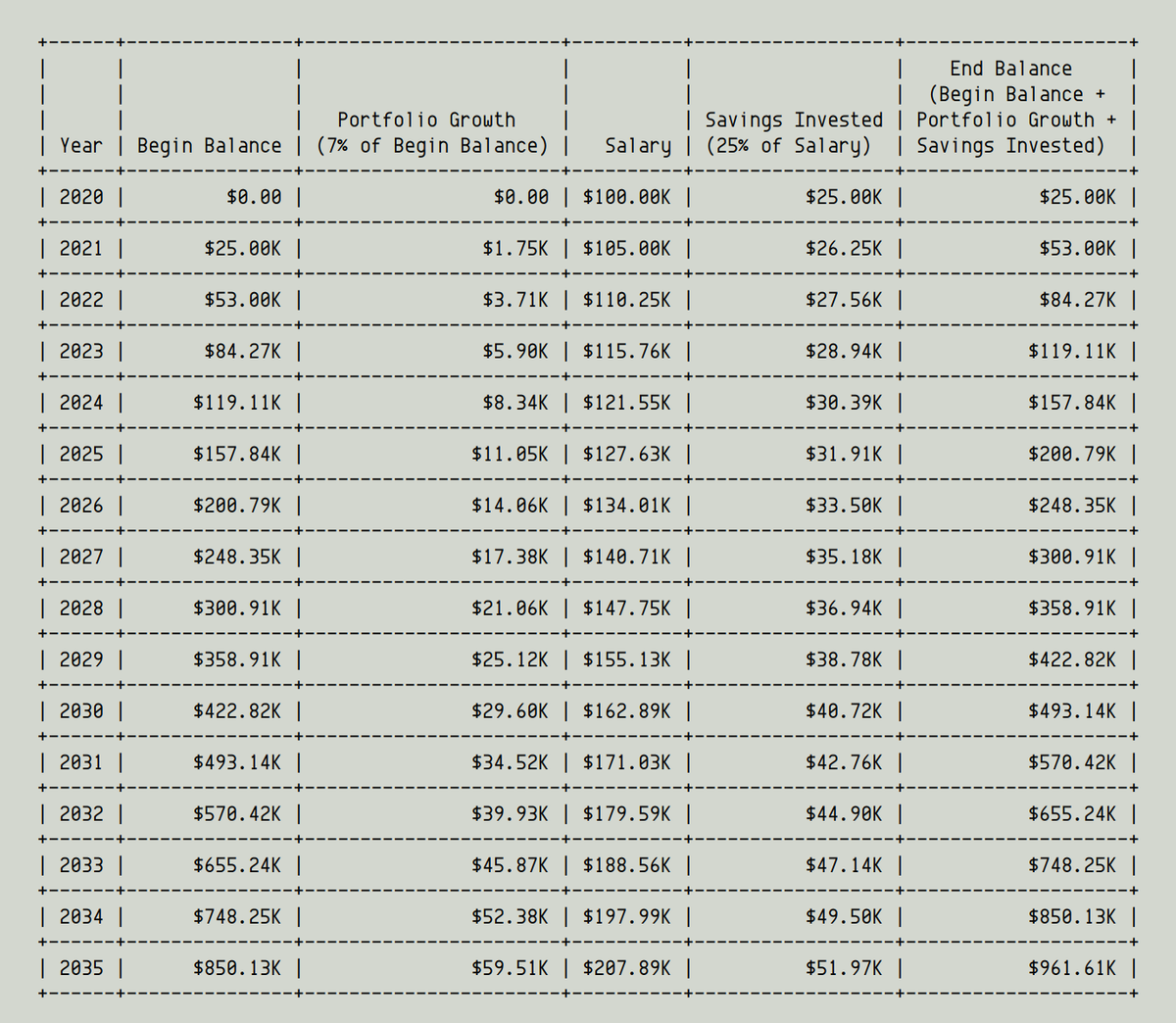
To someone *not* well-versed in geometric sequences, this looks like a simulation problem.
To solve the problem, you have to build a model that projects your future earnings, savings, investments, etc.
Then you simulate the model and get your answer.
Like so:

To someone *not* well-versed in geometric sequences, this looks like a simulation problem.
To solve the problem, you have to build a model that projects your future earnings, savings, investments, etc.
Then you simulate the model and get your answer.
Like so:

20/
In this case, the answer is that you'll have $4.51M at the end of 2050 -- as the simulation above predicts.
We can of course get the answer this way, even if we know nothing of geometric sequences.
In this case, the answer is that you'll have $4.51M at the end of 2050 -- as the simulation above predicts.
We can of course get the answer this way, even if we know nothing of geometric sequences.
21/
But knowing about geometric sequences is a powerful advantage.
It can help us reduce these pages of simulations to a single formula.
This way, we don't need to build a model or run simulations -- our formula will directly give us the 2050 end balance!
Like so:



But knowing about geometric sequences is a powerful advantage.
It can help us reduce these pages of simulations to a single formula.
This way, we don't need to build a model or run simulations -- our formula will directly give us the 2050 end balance!
Like so:




22/
That's the power of understanding geometric sequences and knowing a couple formulas about them.
We can reduce Excel worksheets and financial projections to simple formulas and back-of-the-envelope calculations in many cases.
That's the power of understanding geometric sequences and knowing a couple formulas about them.
We can reduce Excel worksheets and financial projections to simple formulas and back-of-the-envelope calculations in many cases.
23/
Plus, staring at the formula can give us additional insights into how the key variables come together to affect the final answer.
Such insights can significantly improve our understanding of the underlying financial model.
Plus, staring at the formula can give us additional insights into how the key variables come together to affect the final answer.
Such insights can significantly improve our understanding of the underlying financial model.
24/
For example, one glance at the formula above tells us that a 1% increase in investment returns (7% to 8%) will have a much greater impact than a 1% increase in savings (25% to 26%).
This is because the formula *compounds* investment returns, but only *multiplies* savings.
For example, one glance at the formula above tells us that a 1% increase in investment returns (7% to 8%) will have a much greater impact than a 1% increase in savings (25% to 26%).
This is because the formula *compounds* investment returns, but only *multiplies* savings.
25/
One last topic: what if you add up *all* the numbers in a geometric sequence?
But a geometric sequence has infinitely many numbers, right? After all, you can keep generating new numbers simply by multiplying existing numbers by "r".
One last topic: what if you add up *all* the numbers in a geometric sequence?
But a geometric sequence has infinitely many numbers, right? After all, you can keep generating new numbers simply by multiplying existing numbers by "r".
26/
So what does adding up *all* the numbers even mean?
Well, the key idea is that if 0 < r < 1, the numbers will keep becoming smaller and smaller, until they no longer matter as far as the sum is concerned.
Mathematicians call this "convergence".
So what does adding up *all* the numbers even mean?
Well, the key idea is that if 0 < r < 1, the numbers will keep becoming smaller and smaller, until they no longer matter as far as the sum is concerned.
Mathematicians call this "convergence".
27/
In finance, this kind of converged infinite sum is often used in DCF analyses, to value perpetuities and such.
Here's the formula for it, along with an example.
For more details, please see my thread on DCFs:

In finance, this kind of converged infinite sum is often used in DCF analyses, to value perpetuities and such.
Here's the formula for it, along with an example.
For more details, please see my thread on DCFs:
https://twitter.com/10kdiver/status/1292130833273257984


28/
But remember: if r > 1, this convergence won't happen. In this case, adding up *all* the numbers is meaningless -- the sum will just blow up.
But remember: if r > 1, this convergence won't happen. In this case, adding up *all* the numbers is meaningless -- the sum will just blow up.
29/
To sum up (see what I did there!), I want to say: geometric sequences arise all the time in financial calculations.
If you take the time to learn about geometric sequences, you'll understand compounding better. You'll become a better investor.
To sum up (see what I did there!), I want to say: geometric sequences arise all the time in financial calculations.
If you take the time to learn about geometric sequences, you'll understand compounding better. You'll become a better investor.
30/
I hope this helped.
Thanks for reading. Enjoy your weekend!
/End
I hope this helped.
Thanks for reading. Enjoy your weekend!
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh