1/
Get a cup of coffee.
In this thread, I'll help you understand the basics of game theory and Nash Equilibria.
This can help you systematically analyze many economics and business situations.
Get a cup of coffee.
In this thread, I'll help you understand the basics of game theory and Nash Equilibria.
This can help you systematically analyze many economics and business situations.
2/
Since this is a magical topic, we'll set this thread in the Harry Potter universe.
Imagine that you're Ollivander, the wand maker.
You source magical raw materials and make wands out of them. You sell these wands to witches and wizards out of a shop located in Diagon Alley.
Since this is a magical topic, we'll set this thread in the Harry Potter universe.
Imagine that you're Ollivander, the wand maker.
You source magical raw materials and make wands out of them. You sell these wands to witches and wizards out of a shop located in Diagon Alley.

3/
The wand business is highly seasonal.
95% of your sales happen in the two weeks before Hogwarts reopens each year.
Most witches and wizards buy a wand just before their first year at Hogwarts. And they use that wand their whole lives -- so there's not much repeat business.
The wand business is highly seasonal.
95% of your sales happen in the two weeks before Hogwarts reopens each year.
Most witches and wizards buy a wand just before their first year at Hogwarts. And they use that wand their whole lives -- so there's not much repeat business.
4/
And the wand business is a duopoly. There are only 2 major wand makers: (1) you (Ollivander), and (2) your arch rival Gregorovitch.
Every year, the two of you compete fiercely to sell wands to Hogwarts first years. As each student buys exactly 1 wand, it's a zero sum game.
And the wand business is a duopoly. There are only 2 major wand makers: (1) you (Ollivander), and (2) your arch rival Gregorovitch.
Every year, the two of you compete fiercely to sell wands to Hogwarts first years. As each student buys exactly 1 wand, it's a zero sum game.
5/
To convince students to buy their wands from you instead of from Gregorovitch, you can run ads in the Daily Prophet -- the newspaper of the wizarding world.
But of course, these ads cost money. So running them will cut into your profits.
And Gregorovitch can run ads too.
To convince students to buy their wands from you instead of from Gregorovitch, you can run ads in the Daily Prophet -- the newspaper of the wizarding world.
But of course, these ads cost money. So running them will cut into your profits.
And Gregorovitch can run ads too.
6/
Let's say 1,000 first year students enter Hogwarts each year.
If *neither* of you runs ads in the Daily Prophet, these customers will be split 50/50 between the two of you. That is, about 500 students will come to you, and the other 500 will go to Gregorovitch.
Let's say 1,000 first year students enter Hogwarts each year.
If *neither* of you runs ads in the Daily Prophet, these customers will be split 50/50 between the two of you. That is, about 500 students will come to you, and the other 500 will go to Gregorovitch.
7/
What happens if *one* of you runs ads, but the other doesn't?
Well, as you may expect, the one who runs ads will get more customers.
Let's say 900 customers will go to the one who runs ads, and only 100 will go to the one who doesn't.
What happens if *one* of you runs ads, but the other doesn't?
Well, as you may expect, the one who runs ads will get more customers.
Let's say 900 customers will go to the one who runs ads, and only 100 will go to the one who doesn't.
8/
What if *both* of you run ads?
Well, then, your ads will cancel each other out.
You'll each still get 500 customers -- same as if neither of you had run ads.
But in this case, you'll both be poorer as a result of your ad spending.
What if *both* of you run ads?
Well, then, your ads will cancel each other out.
You'll each still get 500 customers -- same as if neither of you had run ads.
But in this case, you'll both be poorer as a result of your ad spending.
9/
Let's say the Daily Prophet charges 5,000 Galleons (the wizard currency) for ads.
Also, let's say both you and Gregorovitch make 25 Galleons on every wand you sell -- not including ad expenses.
Let's say the Daily Prophet charges 5,000 Galleons (the wizard currency) for ads.
Also, let's say both you and Gregorovitch make 25 Galleons on every wand you sell -- not including ad expenses.
10/
Then:
If *neither* one of you runs ads, you each make 12,500 Galleons.
If *one* of you runs ads and the other doesn't, the one who runs ads makes 17,500 Galleons. The one who doesn't makes 2,500 Galleons.
If you *both* run ads, you both make 7,500 Galleons.
Calculations:
Then:
If *neither* one of you runs ads, you each make 12,500 Galleons.
If *one* of you runs ads and the other doesn't, the one who runs ads makes 17,500 Galleons. The one who doesn't makes 2,500 Galleons.
If you *both* run ads, you both make 7,500 Galleons.
Calculations:

11/
Notice how, in this situation, *your* payoff depends on not just your actions, but also on *Gregorovitch's*?
Similarly, *his* payoff depends partly on *your* actions.
Analyzing situations like this -- with cross-dependent payoffs -- is what "game theory" is all about.
Notice how, in this situation, *your* payoff depends on not just your actions, but also on *Gregorovitch's*?
Similarly, *his* payoff depends partly on *your* actions.
Analyzing situations like this -- with cross-dependent payoffs -- is what "game theory" is all about.
12/
Every "game" in game theory has 3 defining characteristics:
1) The "players" who play the game,
2) The "actions" that each player can take, and
3) The "payoffs" that each player gets from the game.
Every "game" in game theory has 3 defining characteristics:
1) The "players" who play the game,
2) The "actions" that each player can take, and
3) The "payoffs" that each player gets from the game.
13/
Our game above has just 2 "players": you (Ollivander) and your rival (Gregorovitch).
But generally speaking, games can have any number of players.
For example, if a third wand maker decided to set up shop, we would suddenly have 3 players. And so on.
Our game above has just 2 "players": you (Ollivander) and your rival (Gregorovitch).
But generally speaking, games can have any number of players.
For example, if a third wand maker decided to set up shop, we would suddenly have 3 players. And so on.
14/
Each player has a set of "actions" open to them.
From these actions, they have to choose one.
In our example, you have 2 actions to choose from: you can either "place ads" or "not place ads". Gregorovitch also has the same 2 actions open to him.
Each player has a set of "actions" open to them.
From these actions, they have to choose one.
In our example, you have 2 actions to choose from: you can either "place ads" or "not place ads". Gregorovitch also has the same 2 actions open to him.
15/
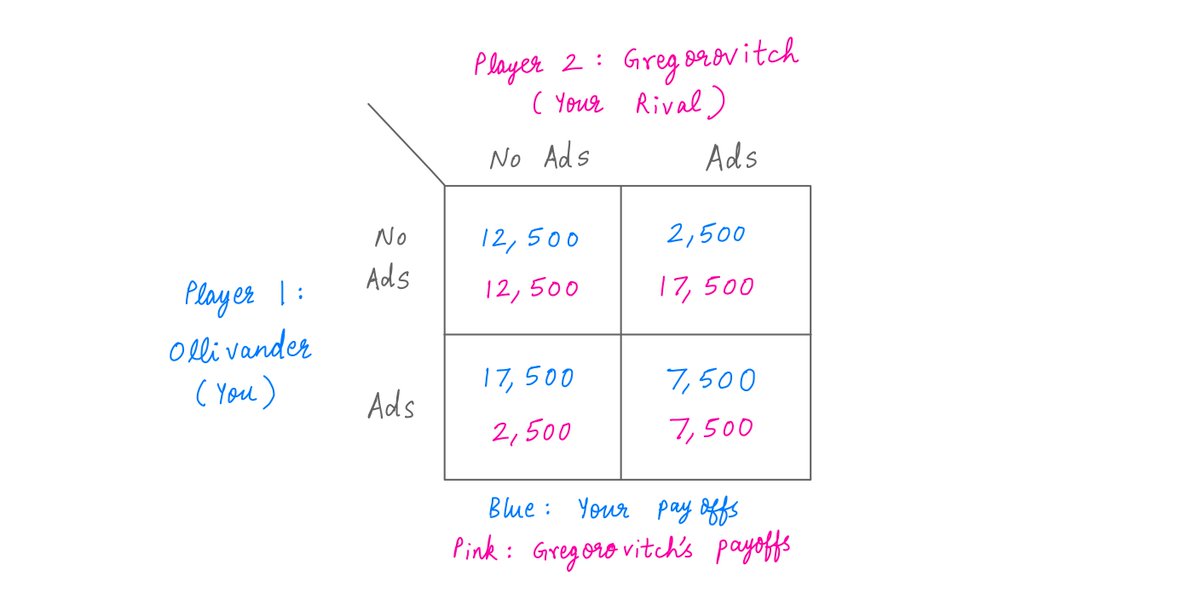
Once each player has chosen an action, the players all receive "payoffs".
The payoff that each player gets depends not just on their own actions, but also on the actions chosen by the other players.
This is usually captured by a "payoff matrix".
Like so:
Once each player has chosen an action, the players all receive "payoffs".
The payoff that each player gets depends not just on their own actions, but also on the actions chosen by the other players.
This is usually captured by a "payoff matrix".
Like so:
16/
As you can see above, the payoff matrix tells you everything there is to know about the game.
It lists the players, the actions open to each player, and the payoffs that each player will get for every possible combination of all the players' actions.
As you can see above, the payoff matrix tells you everything there is to know about the game.
It lists the players, the actions open to each player, and the payoffs that each player will get for every possible combination of all the players' actions.
17/
Once we have the payoff matrix, the next step is to analyze it -- to try and figure out how the game will unfold.
This is where "Nash Equilibrium" comes in.
John Nash, who first proposed it and discovered many of its properties, won a Nobel prize for it in 1994.
Once we have the payoff matrix, the next step is to analyze it -- to try and figure out how the game will unfold.
This is where "Nash Equilibrium" comes in.
John Nash, who first proposed it and discovered many of its properties, won a Nobel prize for it in 1994.

18/
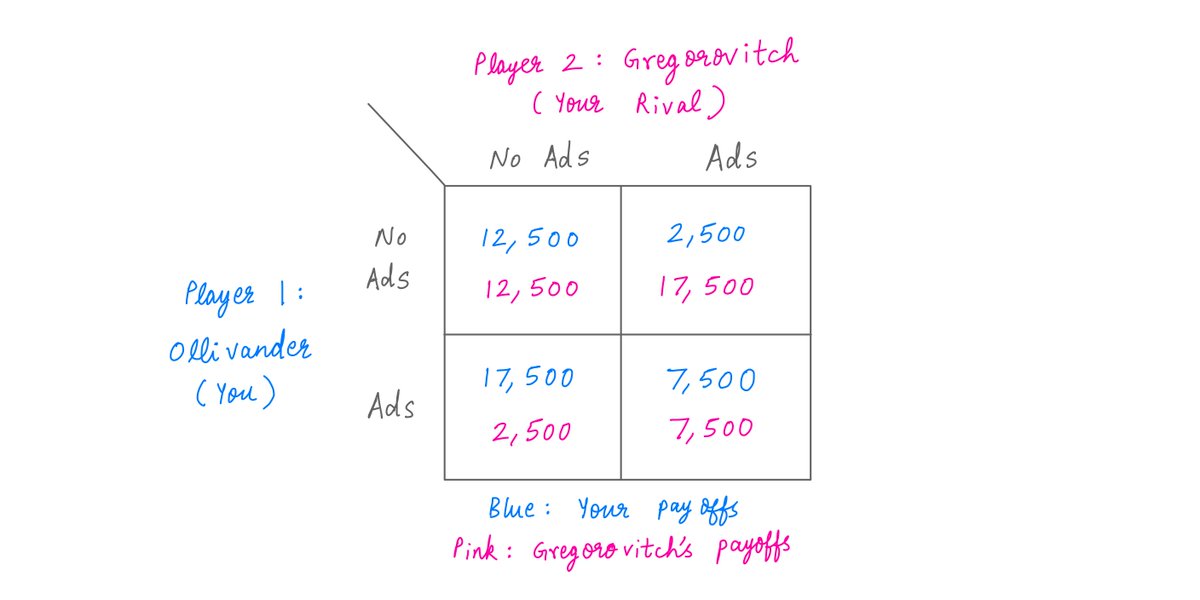
Let's take our example game again.
Suppose Gregorovitch decides not to run ads. In this case, your payoff is 12,500 if you don't run ads and 17,500 if you run ads (from the first column of the payoff matrix below).
Clearly, your optimal strategy in this case is to run ads.
Let's take our example game again.
Suppose Gregorovitch decides not to run ads. In this case, your payoff is 12,500 if you don't run ads and 17,500 if you run ads (from the first column of the payoff matrix below).
Clearly, your optimal strategy in this case is to run ads.
19/
But what if Gregorovitch does the opposite and runs ads?
In this case, your payoff is 2,500 if you don't run ads and 7,500 if you run ads. Clearly, in this case also, your optimal strategy is to run ads.
So, no matter what Gregorovitch does, *you* should be running ads.
But what if Gregorovitch does the opposite and runs ads?
In this case, your payoff is 2,500 if you don't run ads and 7,500 if you run ads. Clearly, in this case also, your optimal strategy is to run ads.
So, no matter what Gregorovitch does, *you* should be running ads.
20/
The same reasoning also applies to Gregorovitch.
No matter what *you* do, *he* will be better served by running ads.
So, in this situation, if the two of you are rational, you'll both end up running ads.
The same reasoning also applies to Gregorovitch.
No matter what *you* do, *he* will be better served by running ads.
So, in this situation, if the two of you are rational, you'll both end up running ads.
21/
Such an outcome -- where your action is the optimal response to his *and* his action is the optimal response to yours -- is called a Nash Equilibrium.
In a Nash Equilibrium, *every* player's chosen action is the optimal response to the actions chosen by the other players.
Such an outcome -- where your action is the optimal response to his *and* his action is the optimal response to yours -- is called a Nash Equilibrium.
In a Nash Equilibrium, *every* player's chosen action is the optimal response to the actions chosen by the other players.
22/
To put it differently: once the players reach a Nash Equilibrium, *no* player has an incentive to change their chosen action.
Why would they? Their current choice is already optimal.
This is why it's called an "equilibrium". Nobody has an incentive to depart from it.
To put it differently: once the players reach a Nash Equilibrium, *no* player has an incentive to change their chosen action.
Why would they? Their current choice is already optimal.
This is why it's called an "equilibrium". Nobody has an incentive to depart from it.
23/
A Nash Equilibrium can sometimes seem paradoxical.
For instance, you and Gregorovitch both run ads in the Nash Equilibrium. In this outcome, you'll both make 7,500 Galleons.
But if you both decided not to run ads, you'd *both* be better off -- with 12,500 Galleons each.
A Nash Equilibrium can sometimes seem paradoxical.
For instance, you and Gregorovitch both run ads in the Nash Equilibrium. In this outcome, you'll both make 7,500 Galleons.
But if you both decided not to run ads, you'd *both* be better off -- with 12,500 Galleons each.
24/
So, by running ads, you're each leaving 5,000 Galleons on the table.
And yet, the outcome where neither of you runs ads is *not* a Nash Equilibrium. The moment one of you decides not to run ads, the other has all the more incentive to run them.
So, by running ads, you're each leaving 5,000 Galleons on the table.
And yet, the outcome where neither of you runs ads is *not* a Nash Equilibrium. The moment one of you decides not to run ads, the other has all the more incentive to run them.
25/
Some games don't have a Nash Equilibrium.
Other games have more than one.
Our example game is special. It has a single, unique Nash Equilibrium. Such games arise frequently in economics and business strategy.
Some games don't have a Nash Equilibrium.
Other games have more than one.
Our example game is special. It has a single, unique Nash Equilibrium. Such games arise frequently in economics and business strategy.
26/
You can use "game theoretic thinking" to help you work out the dynamics of many competitive situations.
For example, in commodity businesses, the optimal pricing strategy of any one company is almost always to try and undercut the others on price.
You can use "game theoretic thinking" to help you work out the dynamics of many competitive situations.
For example, in commodity businesses, the optimal pricing strategy of any one company is almost always to try and undercut the others on price.
27/
Why? Because, in a commodity business, there's no product differentiation. *Only* price matters.
So, even slightly undercutting your competitors can bring you significantly increased unit volumes. This can increase your profits -- provided you keep costs low.
Why? Because, in a commodity business, there's no product differentiation. *Only* price matters.
So, even slightly undercutting your competitors can bring you significantly increased unit volumes. This can increase your profits -- provided you keep costs low.
28/
This is why it's so critical to be a low cost producer in such industries. If not, you end up being the one undercut by the others.
This is why it's so critical to be a low cost producer in such industries. If not, you end up being the one undercut by the others.
29/
By contrast, if a company's products are significantly differentiated in the eyes of consumers (the opposite of a commodity type situation), this can give the company greater pricing power, and hence greater control over its own destiny.
By contrast, if a company's products are significantly differentiated in the eyes of consumers (the opposite of a commodity type situation), this can give the company greater pricing power, and hence greater control over its own destiny.
30/
In game theory terms, the payoffs earned by such companies are strongly correlated to their own actions -- rather than the actions of competitors.
If enough wizards believe that your wands are the best, they won't be swayed much by Gregorovitch's ads.
In game theory terms, the payoffs earned by such companies are strongly correlated to their own actions -- rather than the actions of competitors.
If enough wizards believe that your wands are the best, they won't be swayed much by Gregorovitch's ads.
31/
In many ways, game theoretic thinking is a systematic way to model the power of incentives.
The "payoff matrix" clearly captures each agent's incentives -- and the actions they can take to optimize their own self-interest.
In many ways, game theoretic thinking is a systematic way to model the power of incentives.
The "payoff matrix" clearly captures each agent's incentives -- and the actions they can take to optimize their own self-interest.
32/
As Charlie Munger is fond of saying: Show me the incentives, and I'll show you the outcome.
John Nash might word it slightly differently: Show me the payoff matrix, and I'll show you the Nash Equilibrium.
As Charlie Munger is fond of saying: Show me the incentives, and I'll show you the outcome.
John Nash might word it slightly differently: Show me the payoff matrix, and I'll show you the Nash Equilibrium.
33/
If you're interested in learning more about the applications of game theory to business and finance, I can recommend the book "Competition Demystified", by Bruce Greenwald and Judd Kahn:
amazon.com/Competition-De…
If you're interested in learning more about the applications of game theory to business and finance, I can recommend the book "Competition Demystified", by Bruce Greenwald and Judd Kahn:
amazon.com/Competition-De…
34/
If you read the book, you'll realize that the "Ollivander vs Gregorovitch" game in this thread is just a thinly disguised version of the famous Prisoner's Dilemma.
The book also describes several other games that naturally arise in business -- such as "entry/preemption".
If you read the book, you'll realize that the "Ollivander vs Gregorovitch" game in this thread is just a thinly disguised version of the famous Prisoner's Dilemma.
The book also describes several other games that naturally arise in business -- such as "entry/preemption".
35/
Game theory and Nash Equilibria can seem like esoteric mathematical subjects.
But their fundamental concepts are simple, elegant, and beautiful.
Such mental models have helped sharpen my thinking about strategic interactions. I hope they're useful to you as well.
Game theory and Nash Equilibria can seem like esoteric mathematical subjects.
But their fundamental concepts are simple, elegant, and beautiful.
Such mental models have helped sharpen my thinking about strategic interactions. I hope they're useful to you as well.
36/
If you've reached this point, your strategy is definitely optimal -- and your execution is flawless.
Thanks for reading. Enjoy your weekend!
/End
If you've reached this point, your strategy is definitely optimal -- and your execution is flawless.
Thanks for reading. Enjoy your weekend!
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh