Thread by @prathyvsh

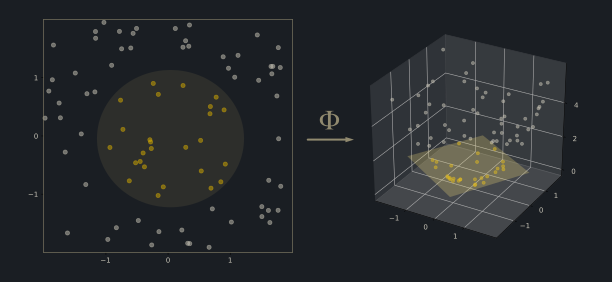
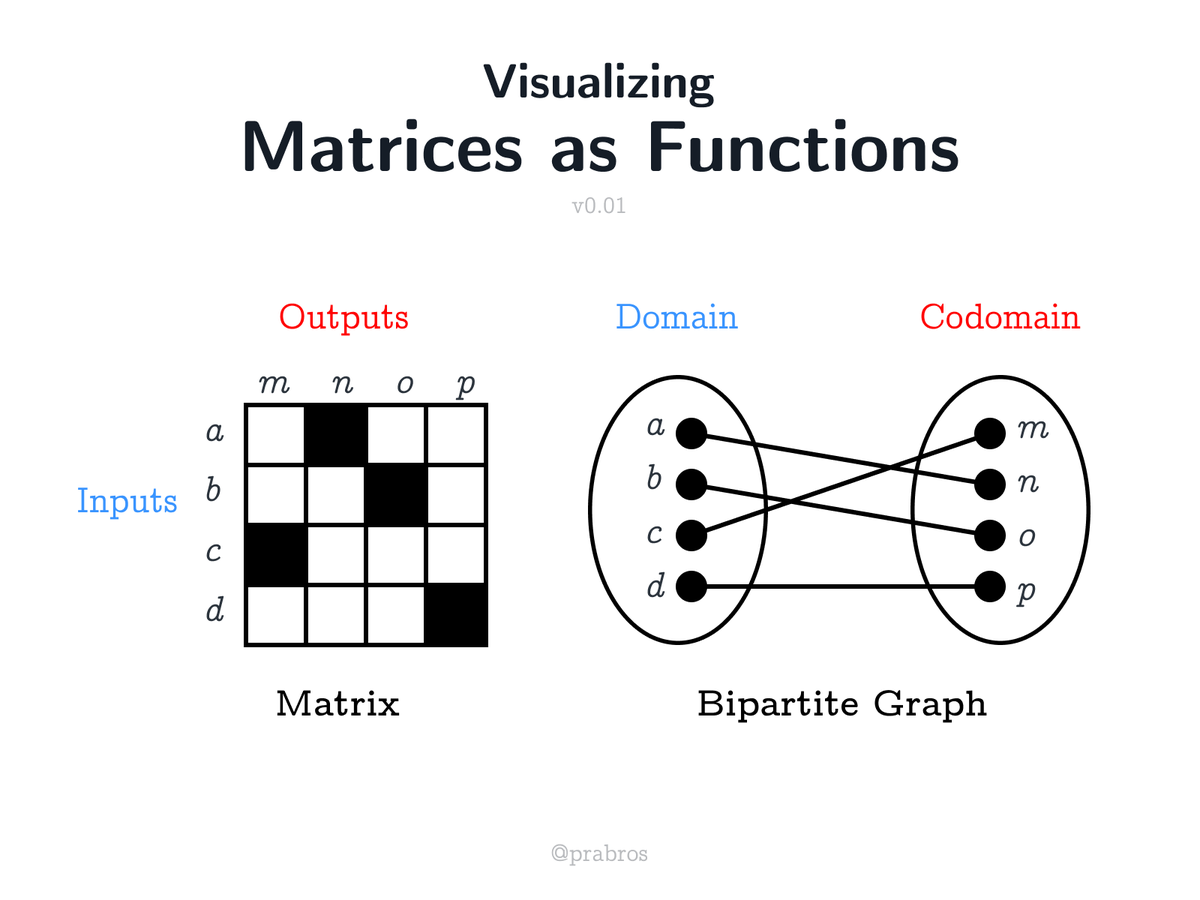
Awesome ontology map of Mathematics by Daniel Tubbenhauer here: dtubbenhauer.com/Talk-Dublin-20…

After my explorations in the last few years, I arrived at an almost same global partitioning except that I had geometry and topology united and number theory featuring as a prominent circle.

I found out previously that Category Theory derives from Kant’s work:

https://twitter.com/prathyvsh/status/1302515424240652288

but looks like Lawvere was attempting to formalize Hegel, who was inspired by Kant’s work!

Have a look at this nLab page to see how deep the rabbit hole runs: ncatlab.org/nlab/show/Scie…

This is in the philosophical realm but use of “relay signs” by artists and mathematicians as sharing the same protogeometry is an interesting take in this article. It draws links between the work of Peirce, Grothendieck, Riemann among others: glass-bead.org/article/multil…

Beautiful set of slides from Daniel Tubbenhaur documenting the history of Category Theory: dtubbenhauer.com/cathistorisch-…

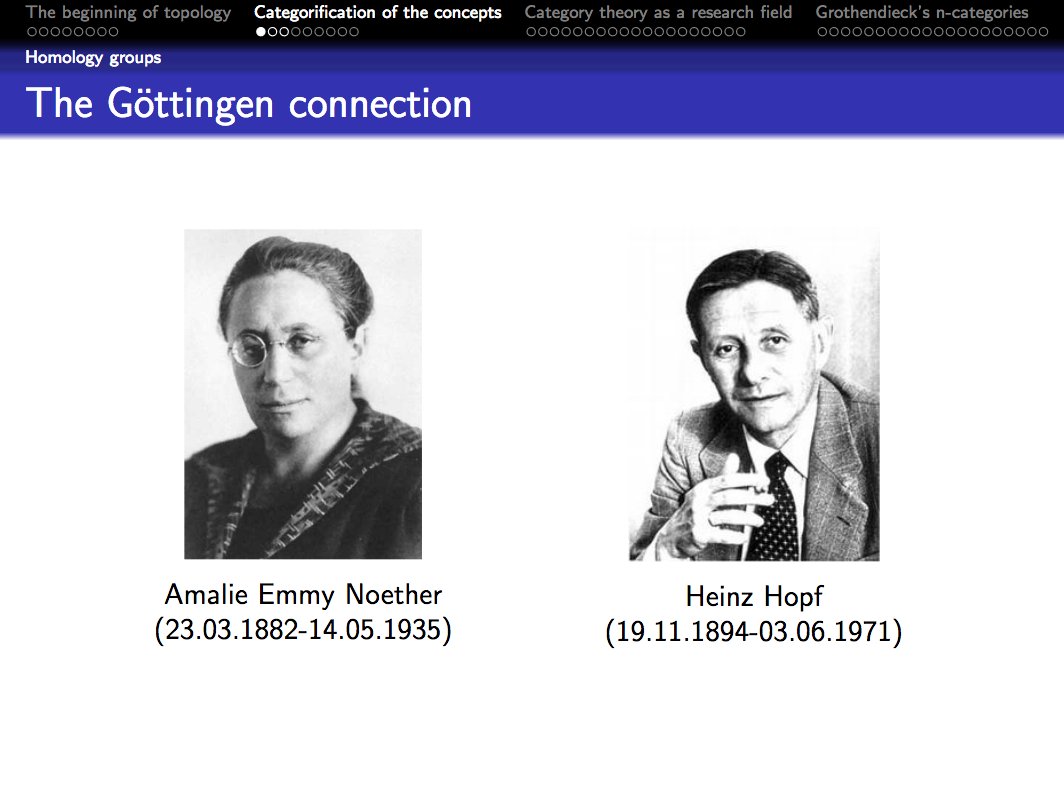
Here is a claim that is usually not heard in circles that deal with Category Theory and Type Theory distinctly: They are the same thing! cs.stackexchange.com/questions/3028…

This is an interesting explanation of how Hegel’s logic of being and nothingness is connected with Category Theory: math.stackexchange.com/questions/2357…

Here’s a visualization of a partial sampling of the network of algebraic structures. Different structures like magma, semigroup, monoid, loop, groups etc. are related to one another by the different properties they trade-off to gain / lose certain characteristics.

I have a latent feeling that algebraic structures have a significant visual signature associated with them even though they are highly abstract and are treated symbolically. Uncovering this will be a huge step in the direction of understanding the geometry / forms of computation.

This is indeed how I grokked the concept of a group. I was investigating the boolean gates and found out that their symmetries were captured with the idea of groups, which made it instantly click for me:

https://twitter.com/prathyvsh/status/1271486696236953601

Thanks for sharing this essay @raghuveerdotnet

@raghuveerdotnet Concept map of the topics explored by Andrée Ehresmann. Her oeuvre is pure 🔥. Such transformative stuff in terms of ambition and scope of what she explores and achieves: ehres.pagesperso-orange.fr

Brendan shared this awesome concept map of algebraic structures earlier in the thread:

https://twitter.com/brendanzab/status/1320512979452882944?s=21

https://t.co/NKOXYSCAUZ

I like this syntactic description used for describing algebraic structures:

https://twitter.com/arthurmilchior/status/1075507270518235139?s=21

https://t.co/0CnmHnIBIw

Really good talk by Alex Simpson: on the foundations of mathematics and computer science. He details beautifully the struggles of supervising a Ph.D. and witnessing how deep fundamental ideas in logic and set theory are intertwined with applied work.

Boris (@AlexanderKatt) just updated his beautiful work on visual category theory with a new chapter on monoids. You guys should totally check it out! boris-marinov.github.io/category-theor…

“Computers and Mathematics: The Search for a Discipline of Computer Science” by Micheal Mahoney is a good read exploring the history of how computation gained a mathematical footing: princeton.edu/~hos/Mahoney/a…

This is a nice series of articles by @jrsinclair on algebraic structures, type classes, and abstract data types: jrsinclair.com/articles/2019/…

Neat talk by Chris Taylor on “The Algebra of Algebraic Types”:

There is a three part companion blog post that elaborates the ideas here: web.archive.org/web/2014021413…

Found out the original PDF version of this map of mathematics:

https://twitter.com/prathyvsh/status/1325836766322987010

on Axel Sarlin’s website: srln.se/mapthematics.p…

A good article on entropy by @aatishb: aatishb.com/entropy/

In the post, entropy is defined as the log of possible of states of micro-configurations while maintaining the macro organization. It made me wonder if it is connected to group theory:

https://twitter.com/prathyvsh/status/1271280943588765702

Discovered the work of Yuli Schreider today. Particularly striking is how systems are described as arising from interactions with the observer, concept of models/frames/theories, and lattice style classification of systems as illustrated in the image: alexei.nfshost.com/biosem/schreid…

Unearthed yet another interesting diagram of order structures. Should really find some time to create a concept lattice out of it like this soon:

https://twitter.com/prathyvsh/status/1332634190903349248

Source: Eric Schechter’s Handbook of Analysis and its Foundations (math.vanderbilt.edu/schectex/ccc/)

Computational Trinitarinism page on nLab has been renamed to Computational Trilogy now with a diagram showing passage from classical version to topological and quantum trilogies! ncatlab.org/nlab/show/comp…

TIL the idea of comonad first appeared in Roger Godement’s book Topologie Algébrique et Théorie des Faisceaux (1958) on Sheaf theory.

Increasingly feeling that learning algebraic geometry might be a necessary step to understand computation.

Source: en.wikipedia.org/wiki/Roger_God…

What is most interesting then is that these abstract ideas in programming languages will start to have a geometrical interpretation. Linas Vepštas has written this beautiful paper where he shows what sheaves look like:

https://twitter.com/prathyvsh/status/1342779419291656193

Finished reading this great article by Saunders Mac Lane (co-inventor of Category Theory) giving a sketch for a philosophy of mathematics: web.archive.org/web/2019100620…

Thanks to @pranavpramod for the share from his exploration of George Lakoff’s work on metaphors.

@pranavpramod He cites Goodman’s paper: jstor.org/stable/2320581 that describes how various philosophies such as Platonism, Empiricism, Logicism, Formalism, and Intuitionism that arose to give an interpretation of the mathematical activity are inadequate and ventures to give his own view.

Saunders Mac Lane outlines how different human activities correspondingly shaped the formation of distinct domains of mathematics such as arithmetic, algebra, analysis, geometry, topology, dynamics, combinatorics etc.

Mac Lane nicely describes how human activities unearth different kinds of concepts (prime numbers, transformations etc) which are then organized under deductive axiomatic systems (Peano arithmetic, Euclidean geometry etc). From this, he proceeds to give his POV of mathematics:

A nice concept map from Mac Lane organizing the concepts of mathematics. He plots how human activities led to the creation of corresponding mathematical concepts.

These are reminiscent of the beautiful diagrams in his book Mathematics, Form and Function:

https://twitter.com/patternatlas/status/1312056411120001025

It is interesting to note that Mac Lane says he doesn’t have an articulate answer to the metaphysical Wigner question of why formal systems of mathematics are unreasonably effective in striking equivalences with phenomena in the real world.

He gives an account of how there exists multiple models to study the same phenomena. I think this applies to cases both within and without mathematics.

He registers his objections with set theory as the grand foundation of mathematics and describes how even within that setting there is the issue of a problem getting the answer Yes/No depending on the underlying model chosen, thereby essentially making the problem undecidable.

These excerpts summarize the position of Saunders Mac Lane: Mathematics as the activity of creating tangible formal systems arising from human activities that capture what is universal both internally as an aspect of human intuition and externally as they map to physical world.

There are some nice descriptions of how mathematical models of space are studied in this paper which has made me eager to study his Mathematical Models of Space (1980): jstor.org/stable/29773730

Looks like another good paper to read along with Mac Lane’s work: “A Mad Day’s Work: From Grothendieck to Connes and Kontsevich — The evolution of concepts of space and symmetry” by Pierre Cartier. Available here: citeseerx.ist.psu.edu/viewdoc/downlo…

Found out about this awesome paper by Barry Mazur on the definition of equality in mathematics. Among other things it contains a discussion on the fitness of formal systems vs. categories for providing foundations for mathematics: people.math.harvard.edu/~mazur/preprin…

Stone Duality marries spatial nature of an algebra to its dynamics described by a coalgebra. I haven't been able to fully understand its ins and outs but here's an introductory paper on it: irif.fr/~mgehrke/Ge11.…

h/t to @deontologistics for sharing this one in a thread of his.

Researched further and found out that Mai Gehrke is a great logician who studies duality as it appears in various forms in mathematics. This Nijmegen inaugural lecture is an accessible introduction to her mathematical philosophy and work: repository.ubn.ru.nl/bitstream/hand…

Mai Gehrke mentions about syntax/semantic duality and its connection to the algebra/geometry duality. This is a very intriguing phenomena in computation which I came across in this paper previously:

https://twitter.com/prathyvsh/status/1344090577088876544

Been reading papers by Arkady Plotnitsky on Riemann’s work and Barry Mazur on Category Theory in parallel. Spotted an uncanny resemblance between the idea of manifold as sociological definition of space by Manin and the idea of object as a network of relationships by Mazur!

Plotnitsky’s work “Bernhard Riemann’s Conceptual Mathematics and the Idea of Space” can be found here: web.ics.purdue.edu/~plotnits/PDFs… and Mazur’s work here:

https://twitter.com/prathyvsh/status/1406666444830646273

Also adding Manin’s “Georg Cantor and His Heritage”: arxiv.org/pdf/math/02092…

Just love the fact that the papers of Per Martin-Löf are available at one place: github.com/michaelt/marti…

Some ground breaking stuff there touching upon constructive mathematics ∩ logic ∩ computation ∩ philosophy!

Sequent Calculus is a formal argumentation system devised by Gerhard Gentzen for tracking proof reductions: en.wikipedia.org/wiki/Sequent_c…

It visualizes how you start from axioms and arrive at particular conclusions. There’s good scope for UI designers to build nice interfaces for it.

There was qualitative improvement in my skill in understanding programming language theory papers after working out how the sequent calculus system works. This is a really good interactive tutorial that set me on this path: logitext.mit.edu/tutorial

Ever since I read @coecke’s alternative Gospel paper: arxiv.org/abs/1307.4038 I am a strong believer that functorial string diagrams will take us much further in “seeing” what programs do rather than simulating them in our heads. These images here were a big aha! moment for me.

@coecke Here is a recent illustration by @danghica, Mario Álvarez-Picallo, David Sprunger, and Fabio Zanasi elucidating the link between automatic differentiation and string diagrams:

https://twitter.com/danghica/status/1422120075868483584

Paper: arxiv.org/pdf/2107.13433…

If you have some cursory knowledge about Lambda Calculus, Type Theory, and Sequent Calculus, this is a really good introductory lecture from Xavier Leroy (co-creator of OCaml) on the Curry-Howard correspondence.

Programming = Proving?: college-de-france.fr/site/en-xavier…

This is an interesting read from @getjonwithit that maps homotopy type theory to Wolfram multiway formalism to arrive at a geometric conception of the Church-Turing thesis: wolframphysics.org/bulletins/2020…

Fun little poetic exercise to understand the Galois connection!

“A Galois Connection in the Social Network” by @JimPropp: faculty.uml.edu/jpropp/galois.…

@JimPropp Petition to expand the Curry Howard Lambek correspondence: en.wikipedia.org/wiki/Curry%E2%… to Curry Howard Lambek Stone Scott Grothendieck Voevodsky Correspondence.

Fun comic on the time travel aspect of Law of Excluded Middle in the paper “Duality in Action” by Paul Downen and Zeno Ariola. The paper is also interesting as it derives a symmetrical calculus by taking a dialogical interpretation of constructive logic: ix.cs.uoregon.edu/~pdownen/publi…

A nice thread by @plt_abbie on type theory and Curry-Howard-Lambek correspondence:

https://twitter.com/plt_abbie/status/1384672238276915210

TIL Haskell Curry (Combinatory Logic), Gerhard Gentzen (Proof Theory) and Saunders Mac Lane (Category Theory) were doctoral students at Hilbert’s Göttingen! What seems even lesser known is that Mac Lane did a dissertation in “algebra of proofs”.

Source: lmcs.episciences.org/5646/pdf

Pathways of Deduction by @acarbone16 has been a thoroughly formative read in my logical research! Alessandra brings ideas from structural proof theory and reveals some striking connections in geometry ∩ logic ∩ biology. Highly recommended read! ihes.fr/~carbone/paper…

Really nice example that when you shift the framework from classical logic to constructive logic you get diagonalization from Russell’s paradox.

Now mulling about if/how I can connect Gödel incompleteness and Halting problem with this one:

https://twitter.com/Intell3ctualize/status/1417918649302650880

A super nice glossary of algebraic structures from Hubert Kaeslin! Source: cambridge.org/be/files/1413/…

I need to start a thread on paradoxes proper, but adjoining a few papers that I spotted that takes a unified approach to understand paradoxes. First up is Lawvere’s fixed point theorem:

https://twitter.com/shachaf/status/1183934586775957504

The original paper by William Lawvere called “Diagonal Arguments and Cartesian Closed Categories” is available here: tac.mta.ca/tac/reprints/a…

Yanofsky has written this paper unifying various fixed point theorems called “A Universal Approach to Self-Referential Paradoxes, Incompleteness and Fixed Points”: arxiv.org/pdf/math/03052…

Here a unifying construction is given for Liar paradox, Cantor’s diagonalization, Russell’s paradox, Richard’s paradox, Grelling’s paradox, Incompleteness theorems, Halting problem, Rice Theorem, Löb’s Paradox, Parikh sentences, Von Neumann self-reproducing machines and more!

Yanofsky gave a talk on this work in July 2021 as a part of celebrating 90 years of Gödel’s Incompleteness Theorems. “Diagonalization, Fixed Points, and Self-reference”:

If you enjoy such works be sure to check out Yanofsky’s book which outlines the limits of what is achievable with human reason. “The Outer Limits of Reason: What Science, Mathematics, and Logic Cannot Tell Us”: amzn.to/3EU3Wdu

Yanofsky also has a book coming out on Theoretical Computer Science treating it from a Category Theory viewpoint: sci.brooklyn.cuny.edu/~noson/TCStext…

What prompted this curation on fixed points is running across these resources:

1/ Substructural fixed-point theorems and the diagonal argument (2021): arxiv.org/abs/2110.00239

2/ An Order-Theoretic Account of Some Set-Theoretic Paradoxes (2011): projecteuclid.org/journals/notre…

Adele (@AdeleDeweyLopez) just did an awesome visual exposition of the Chu spaces! Chu spaces are structures that allows you to encode many mathematical structures and connects with so many dualities spread across the spectrum of math: adelelopez.com/chu-are-you

@AdeleDeweyLopez I will write a thread on this later but transitive reduction on a graph generates a partial order on which we can do a transitive closure to generate all the accessible locations. This type of closure ⇌ kernel transformations can be studied using an adjacency matrix:

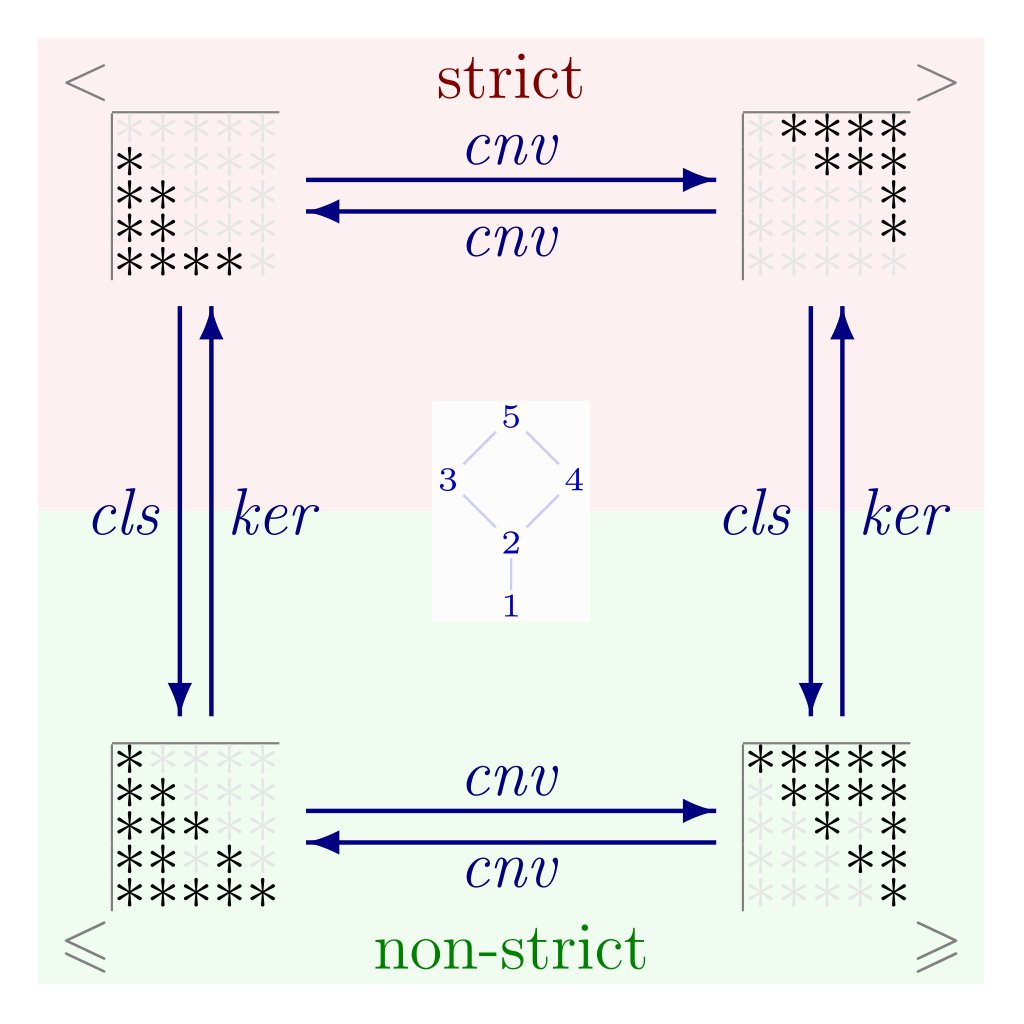
@AdeleDeweyLopez This matrix approach is additive/constructive building structures bottom up. But I love how Chu space is subtractive/predicative: the most unstructured one has the most amount of information and more structured ones are progressively generated top down with logical constraints!

@AdeleDeweyLopez This is a neat introduction to the field of program analysis by @trupill: gist.github.com/serras/4370055… Gives a neat intuition on how abstract interpretation acts as a unifying lens on the whole field!

Gets a bit technical towards the end but this is a really good introductory talk on adjunctions:

https://twitter.com/maineframeworks/status/1465500638389878792?s=21

A pretty interesting talk here which I should probably also add to the history of logic thread — How Gödel Discovered his Incompleteness Theorems by John von Plato:

Wonder why this observation wasn’t woven into this thread but noticed again today while browsing Wiki that Mac Lane and Eilenberg (originators of category theory) thought of their work as continuation of Klein’s Erlangen programme:

https://twitter.com/prathyvsh/status/1312714453079584768

Neat observations on Galois connections as they play out in many places by @runarorama: blog.higher-order.com/blog/2014/12/2…

@runarorama When to be disciplined and when to unleash free reign in your field of operation is a great informing principle if one can figure out the various conceptual structures and computational processes this idea seeps through.

@runarorama Awesome paper showing analogies between discrete/continuous domains:

https://twitter.com/LdaFCosta/status/1454520031132459008

h/t @Xirong7 for notification.

It’s really intriguing as I started seeing how Fourier Transform style decomposition into factors is a pervasive technique throughout maths.

@runarorama @Xirong7 Some amazing visual notes taken by Peter Morcos when learning from @johncarlosbaez’ Applied Category Theory tutorial (2018): azimuthproject.org/azimuth/show/P…

This is perhaps one of the most well organized schemata of how algebraic structures are related out there: observablehq.com/@diracshore/al…

Needs more labels to show what tradeoffs are made to arrive at a particular structure, but really neat effort here!