1/
Get a cup of coffee.
In this thread, I'll walk you through the Rule of 72 -- and related "mental math tricks" for investors.
Get a cup of coffee.
In this thread, I'll walk you through the Rule of 72 -- and related "mental math tricks" for investors.
2/
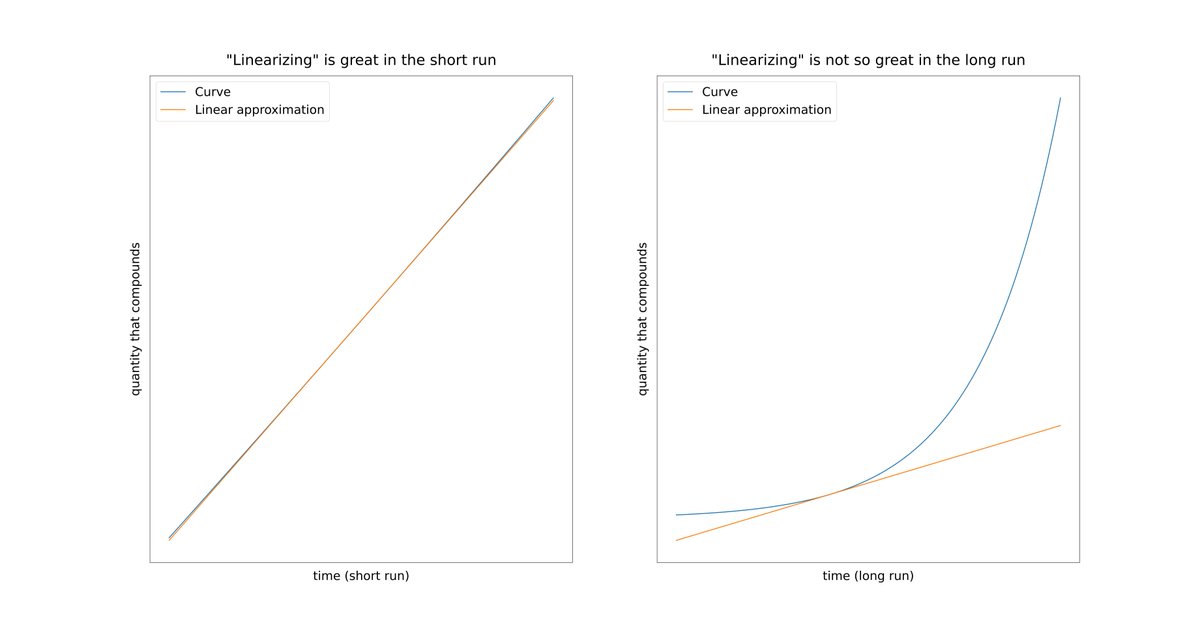
As humans, we tend to think *linearly*.
When we see a curve, we like to mentally approximate it by a straight line.
This helps us cope with changes in the world around us. Changes that happen a *constant* pace. Changes that don't need our attention for very long.
As humans, we tend to think *linearly*.
When we see a curve, we like to mentally approximate it by a straight line.
This helps us cope with changes in the world around us. Changes that happen a *constant* pace. Changes that don't need our attention for very long.
3/
But in finance/investing, we need to think *exponentially*, not *linearly*.
Money compounds. Growth doesn't happen at a constant pace; it *accelerates* over time.
Most of us are not programmed to intuitively "get" compounding -- over the long run.
But in finance/investing, we need to think *exponentially*, not *linearly*.
Money compounds. Growth doesn't happen at a constant pace; it *accelerates* over time.
Most of us are not programmed to intuitively "get" compounding -- over the long run.
4/
So we need some "mental shorthands".
Rules of thumb that help us develop intuition about exponential growth.
Tricks that help us do "compounding math" in our head.
One such trick is to think of compounding as a process that *doubles* our money every so many years.
So we need some "mental shorthands".
Rules of thumb that help us develop intuition about exponential growth.
Tricks that help us do "compounding math" in our head.
One such trick is to think of compounding as a process that *doubles* our money every so many years.
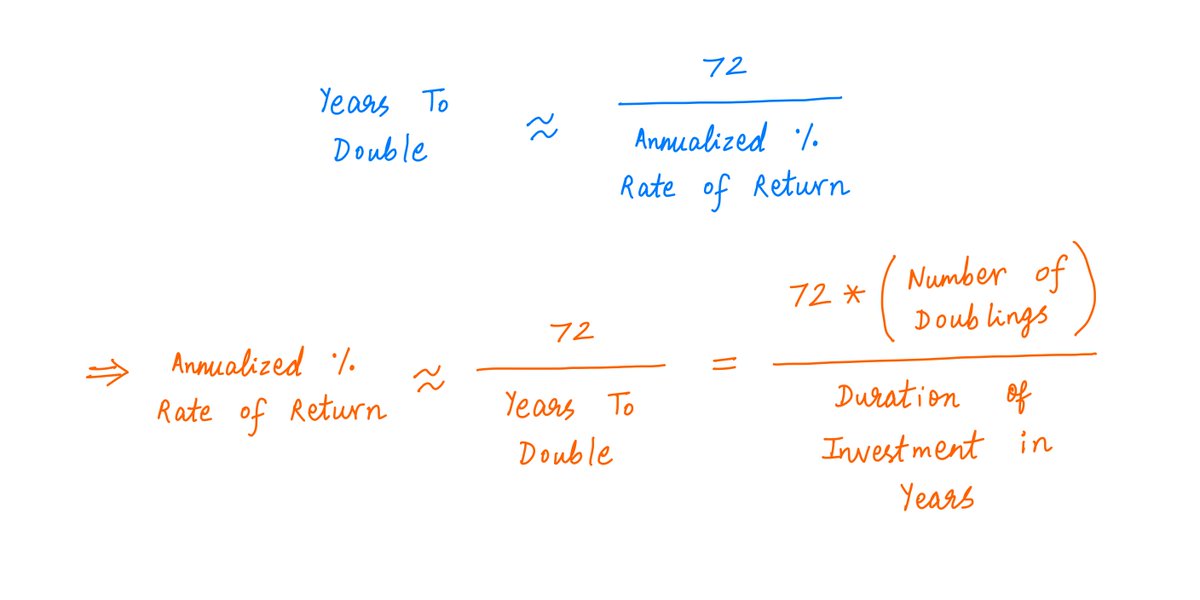
5/
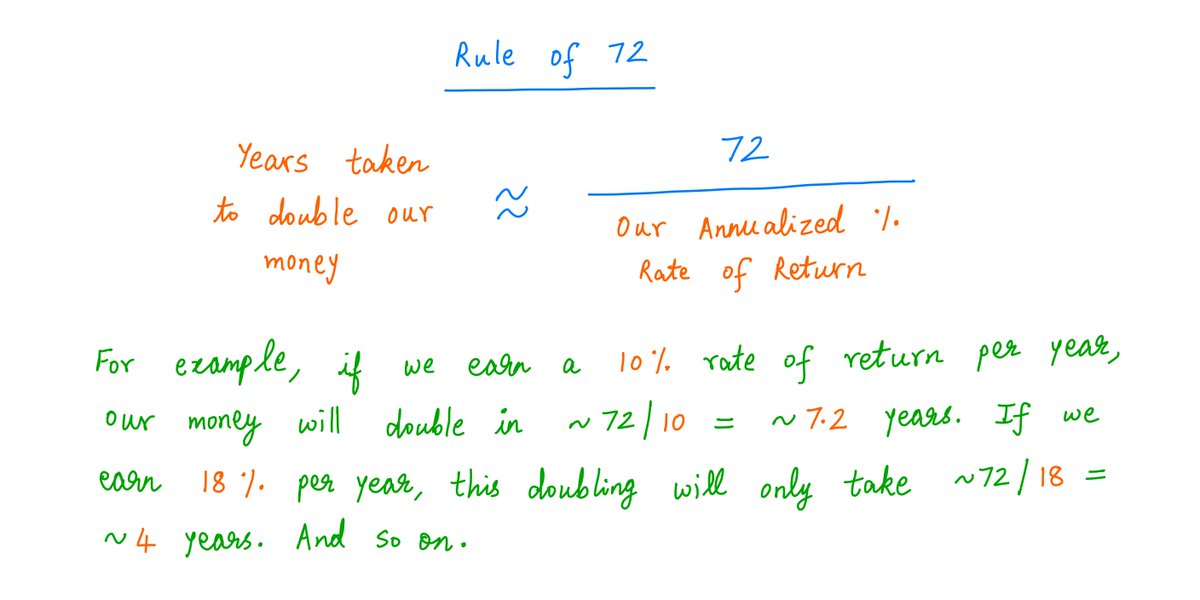
So the question is: how long does the compounding process take to double our money?
The Rule of 72 gives us a simple approximate formula for this:
So the question is: how long does the compounding process take to double our money?
The Rule of 72 gives us a simple approximate formula for this:
6/
As you can see, our rate of return appears in the *denominator* of the Rule of 72.
This makes intuitive sense: as our return increases, it takes less time to double our money.
As you can see, our rate of return appears in the *denominator* of the Rule of 72.
This makes intuitive sense: as our return increases, it takes less time to double our money.
7/
Also note: the Rule of 72 doesn't need to know *how much* money we start with.
For example, suppose our return is 9% per year. The rule then says we'll double our money in approximately 72/9 = 8 years.
Also note: the Rule of 72 doesn't need to know *how much* money we start with.
For example, suppose our return is 9% per year. The rule then says we'll double our money in approximately 72/9 = 8 years.
8/
If we start with $100, we'll have $200 in ~8 years.
If we start with $1M, we'll have $2M in ~8 years.
It doesn't matter how much we start with. Whatever it is, it gets doubled in ~8 years -- as long as we can compound at 9% per year. That's the Rule of 72.
If we start with $100, we'll have $200 in ~8 years.
If we start with $1M, we'll have $2M in ~8 years.
It doesn't matter how much we start with. Whatever it is, it gets doubled in ~8 years -- as long as we can compound at 9% per year. That's the Rule of 72.
9/
The Rule of 72 encourages us to *think* in terms of repeatedly doubling our money.
This kind of thinking is powerful. It can help us do various compounding calculations just mentally -- no need to reach for a calculator or computer.
The Rule of 72 encourages us to *think* in terms of repeatedly doubling our money.
This kind of thinking is powerful. It can help us do various compounding calculations just mentally -- no need to reach for a calculator or computer.
10/
For example, in this excellent ~40 min video, @MohnishPabrai demonstrates one such calculation.
At the age of 18, Mohnish's daughter Monsoon (@Typhoon_Girl) did an internship. From this, she saved $5K.
For example, in this excellent ~40 min video, @MohnishPabrai demonstrates one such calculation.
At the age of 18, Mohnish's daughter Monsoon (@Typhoon_Girl) did an internship. From this, she saved $5K.
11/
She gave this $5K to Mohnish to invest.
Mohnish -- being the skilled investor he is -- feels confident that he can compound this money at 15% per year for 50 years.
The question is: at the end of 50 years (when Monsoon turns ~68), what would this $5K have grown into?
She gave this $5K to Mohnish to invest.
Mohnish -- being the skilled investor he is -- feels confident that he can compound this money at 15% per year for 50 years.
The question is: at the end of 50 years (when Monsoon turns ~68), what would this $5K have grown into?
12/
We can do this calculation mentally -- just by thinking in doublings and using the Rule of 72.
Step 1. At our 15% per year return, the Rule of 72 says it will take roughly 72/15 = about 5 years to double Monsoon's money.
We can do this calculation mentally -- just by thinking in doublings and using the Rule of 72.
Step 1. At our 15% per year return, the Rule of 72 says it will take roughly 72/15 = about 5 years to double Monsoon's money.
13/
Step 2. Over 50 years, that means the money will get doubled 10 times.
(50 years total)/(5 years per doubling) = 10 doublings.
Step 2. Over 50 years, that means the money will get doubled 10 times.
(50 years total)/(5 years per doubling) = 10 doublings.
14/
Step 3: From the "doubling table" below, we can see that after 10 doublings, every $1 turns into $1024. That's roughly a 1000x growth.
As Monsoon originally started with $5K, she will therefore end up with roughly 1000 * $5K = ~$5M at the end of the 50-year period.
Step 3: From the "doubling table" below, we can see that after 10 doublings, every $1 turns into $1024. That's roughly a 1000x growth.
As Monsoon originally started with $5K, she will therefore end up with roughly 1000 * $5K = ~$5M at the end of the 50-year period.

15/
In this way, we can use the Rule of 72 and the process of "thinking in doublings" to work out approximately how much a given sum of money will grow into after many years of compounding.
Here's a quick summary of the steps involved:
In this way, we can use the Rule of 72 and the process of "thinking in doublings" to work out approximately how much a given sum of money will grow into after many years of compounding.
Here's a quick summary of the steps involved:

16/
We can also use these ideas to quickly estimate our rate of return from an investment.
For example, let's take the excellent book "100 baggers" by @chriswmayer. The book is about companies that have delivered superb returns to long term shareholders. amazon.com/100-Baggers-St…
We can also use these ideas to quickly estimate our rate of return from an investment.
For example, let's take the excellent book "100 baggers" by @chriswmayer. The book is about companies that have delivered superb returns to long term shareholders. amazon.com/100-Baggers-St…
17/
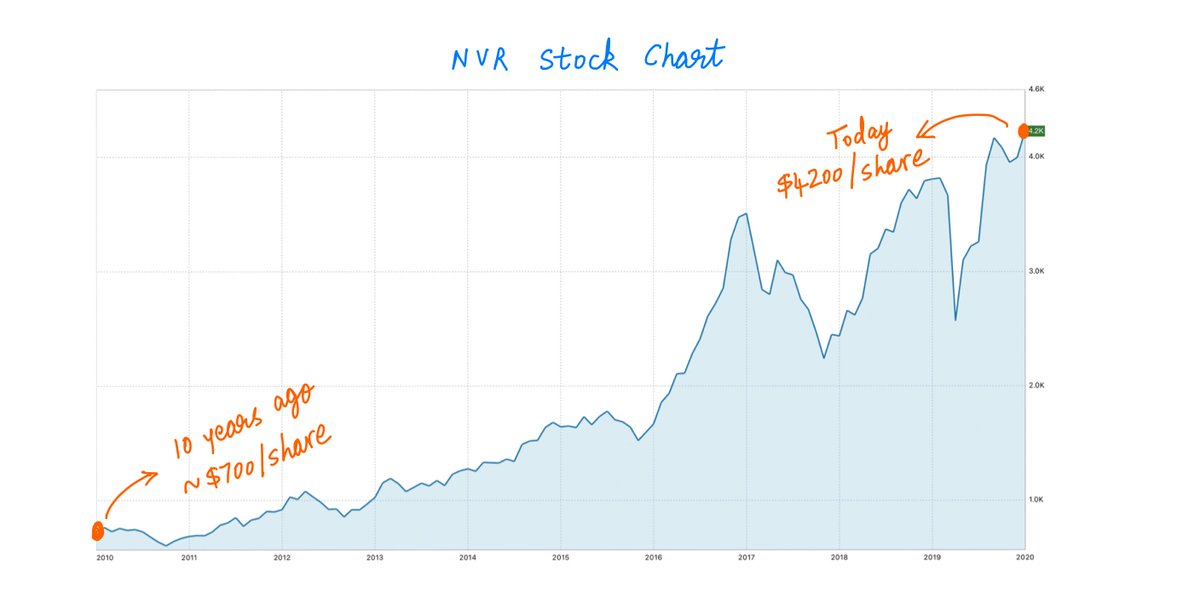
Let's take one example from the book: NVR, a home builder.
Suppose we bought this stock about 10 years ago. At the time, the stock was at ~$700/share. Today, it's at ~$4200/share.
Suppose we held our shares over these 10 years. What's our annualized return?
Let's take one example from the book: NVR, a home builder.
Suppose we bought this stock about 10 years ago. At the time, the stock was at ~$700/share. Today, it's at ~$4200/share.
Suppose we held our shares over these 10 years. What's our annualized return?
18/
Again, we can estimate this using the idea of doublings and the Rule of 72.
Step 1. $700/share to $4200/share is a ~6x growth.
We know that "2 doublings" means ~4x growth and "3 doublings" means ~8x growth. So our ~6x growth is roughly 2.5 doublings.
Again, we can estimate this using the idea of doublings and the Rule of 72.
Step 1. $700/share to $4200/share is a ~6x growth.
We know that "2 doublings" means ~4x growth and "3 doublings" means ~8x growth. So our ~6x growth is roughly 2.5 doublings.
19/
Step 2. These ~2.5 doublings have happened over 10 years. So 1 doubling has taken roughly 10/2.5 = 4 years.
Step 3. From the Rule of 72, we calculate our annualized percentage rate of return to be roughly 72/(years to double) = 72/4 = ~18%.
Step 2. These ~2.5 doublings have happened over 10 years. So 1 doubling has taken roughly 10/2.5 = 4 years.
Step 3. From the Rule of 72, we calculate our annualized percentage rate of return to be roughly 72/(years to double) = 72/4 = ~18%.
20/
Key lesson: With practice, the Rule of 72 and "thinking in doublings" can help us do "compounding math" mentally.
This can give us a real appreciation for exponential growth and the power of compounding -- what Einstein called the 8'th wonder of the world.
Key lesson: With practice, the Rule of 72 and "thinking in doublings" can help us do "compounding math" mentally.
This can give us a real appreciation for exponential growth and the power of compounding -- what Einstein called the 8'th wonder of the world.
21/
Buffett habitually thinks like this. His hurdle rate for stocks is around 15% per year -- that's a doubling every 5 years.
Early in life, he realized that if he could keep this up for 80 years or so, he would double his money 80/5 = 16 times.
Buffett habitually thinks like this. His hurdle rate for stocks is around 15% per year -- that's a doubling every 5 years.
Early in life, he realized that if he could keep this up for 80 years or so, he would double his money 80/5 = 16 times.
22/
That's a 2^16 = ~65000x growth.
Over a lifetime, this growth would turn $10K into ~$650M -- a phenomenal result achieved by steady compounding.
And we know Buffett has done even better than that -- because his returns have been better than 15% per year.
That's a 2^16 = ~65000x growth.
Over a lifetime, this growth would turn $10K into ~$650M -- a phenomenal result achieved by steady compounding.
And we know Buffett has done even better than that -- because his returns have been better than 15% per year.
23/
Armed with mental techniques like the Rule of 72 and "thinking in doublings", even seemingly ordinary people can achieve extraordinary results -- if they're patient and disciplined.
For example, here's an inspiring story from "The Psychology of Money" by @morganhousel:
Armed with mental techniques like the Rule of 72 and "thinking in doublings", even seemingly ordinary people can achieve extraordinary results -- if they're patient and disciplined.
For example, here's an inspiring story from "The Psychology of Money" by @morganhousel:

24/
In addition to Mohnish's video above, I also recommend this ~21 min video by @FocusedCompound.
Here, Andrew and Geoff discuss the Rule of 240 -- a variant of the Rule of 72 for "10x-ing" (rather than merely doubling) one's money.
In addition to Mohnish's video above, I also recommend this ~21 min video by @FocusedCompound.
Here, Andrew and Geoff discuss the Rule of 240 -- a variant of the Rule of 72 for "10x-ing" (rather than merely doubling) one's money.
25/
Thanks for reading to the end of another long thread.
Readers like you double my joy every week on Twitter!
Stay safe. Enjoy your weekend!
/End
Thanks for reading to the end of another long thread.
Readers like you double my joy every week on Twitter!
Stay safe. Enjoy your weekend!
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh