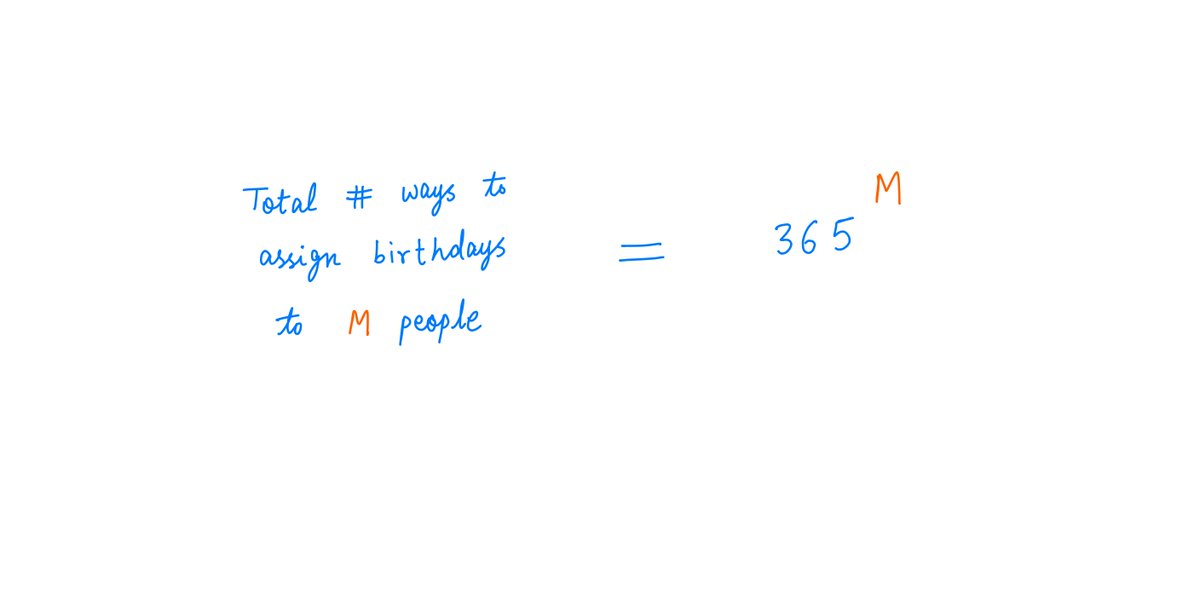1/
Get a cup of coffee.
Let's talk about the Birthday Paradox.
This is a simple exercise in probability.
But from it, we can learn so much about life.
About strategic problem solving.
About non-linear thinking -- convexity, concavity, S curves, etc.
So let's dive in!
Get a cup of coffee.
Let's talk about the Birthday Paradox.
This is a simple exercise in probability.
But from it, we can learn so much about life.
About strategic problem solving.
About non-linear thinking -- convexity, concavity, S curves, etc.
So let's dive in!
2/
Suppose we came across a "30 under 30" Forbes list.
The list features 30 highly accomplished people.
What are the chances that at least 2 of these 30 share the same birthday?
Same birthday means they were born on the same day (eg, Jan 5). But not necessarily the same year.
Suppose we came across a "30 under 30" Forbes list.
The list features 30 highly accomplished people.
What are the chances that at least 2 of these 30 share the same birthday?
Same birthday means they were born on the same day (eg, Jan 5). But not necessarily the same year.

3/
What if it was a "40 under 40" list?
Or a "50 under 50" list?
Or in general: if we put M people on a list, what are the chances that *some* 2 of them will share the same birthday?
What if it was a "40 under 40" list?
Or a "50 under 50" list?
Or in general: if we put M people on a list, what are the chances that *some* 2 of them will share the same birthday?
4/
Clearly, this is an exercise in probability.
To solve it, we'll assume 3 things:
1. No Feb 29 birthdays,
2. Each person on our list is *equally likely* to be born on any one of the other 365 days (Jan 1 to Dec 31), and
3. The birthdays are all independent of each other.
Clearly, this is an exercise in probability.
To solve it, we'll assume 3 things:
1. No Feb 29 birthdays,
2. Each person on our list is *equally likely* to be born on any one of the other 365 days (Jan 1 to Dec 31), and
3. The birthdays are all independent of each other.
5/
Another way to state the problem:
We have M people, and a 365-sided fair die.
Each person is allowed to roll the die once -- and is thereby assigned a number between 1 and 365 (both inclusive).
What are the chances that *some* 2 people will get assigned the same number?
Another way to state the problem:
We have M people, and a 365-sided fair die.
Each person is allowed to roll the die once -- and is thereby assigned a number between 1 and 365 (both inclusive).
What are the chances that *some* 2 people will get assigned the same number?
6/
Clearly, as the number of people (M) increases, so does the likelihood that *some* 2 of them will share the same birthday.
For example, suppose we have just 2 people on our list. That is, M=2. There's only a "1 in 365" (~0.27%) chance that they'll share the same birthday.
Clearly, as the number of people (M) increases, so does the likelihood that *some* 2 of them will share the same birthday.
For example, suppose we have just 2 people on our list. That is, M=2. There's only a "1 in 365" (~0.27%) chance that they'll share the same birthday.
7/
But suppose we have 366 people (ie, M = 366).
Clearly, they can't *all* have different birthdays. There are only 365 days to go around. (Remember: no Feb 29 birthdays.)
So, there's a 100% chance that *some* 2 of them will share the same birthday.
But suppose we have 366 people (ie, M = 366).
Clearly, they can't *all* have different birthdays. There are only 365 days to go around. (Remember: no Feb 29 birthdays.)
So, there's a 100% chance that *some* 2 of them will share the same birthday.
8/
So, as M goes from 2 to 366, our probability of encountering "birthday buddies" goes from ~0.27% to 100%.
At what point do you think the probability crosses 50%? 75%? 90%? 99%?
So, as M goes from 2 to 366, our probability of encountering "birthday buddies" goes from ~0.27% to 100%.
At what point do you think the probability crosses 50%? 75%? 90%? 99%?
9/
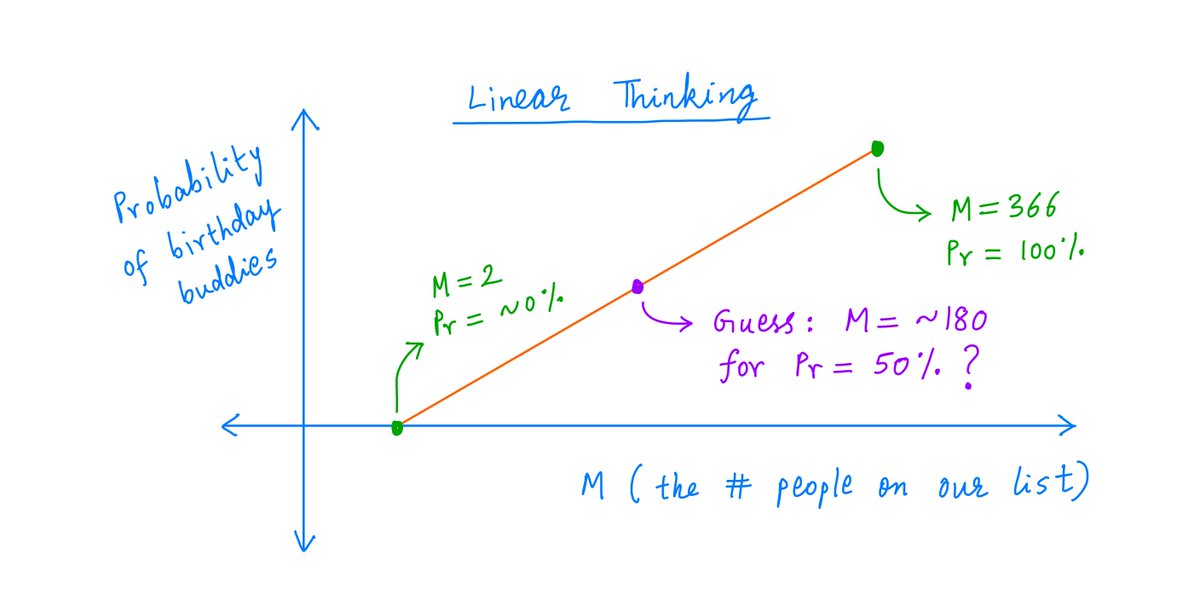
When asked questions like this, most people's first reaction is to *think linearly*.
At M = 2, the probability of birthday buddies is ~0%. By the time M = 366, it's 100%.
So the 50% mark should be crossed roughly halfway between 2 and 366, right? Say, at M = 180 or so?
When asked questions like this, most people's first reaction is to *think linearly*.
At M = 2, the probability of birthday buddies is ~0%. By the time M = 366, it's 100%.
So the 50% mark should be crossed roughly halfway between 2 and 366, right? Say, at M = 180 or so?
10/
The right answer, it turns out, is just M = 23.
We need just 23 people on the list to give us a more than 50% chance of encountering birthday buddies.
That's the Birthday Paradox.
Our intuition, based on *linear thinking*, often misguides us in probabilistic settings.
The right answer, it turns out, is just M = 23.
We need just 23 people on the list to give us a more than 50% chance of encountering birthday buddies.
That's the Birthday Paradox.
Our intuition, based on *linear thinking*, often misguides us in probabilistic settings.
11/
Charlie Munger's "Invert, Always Invert" mantra comes in handy when analyzing the birthday paradox.
Instead of asking "what's the probability of encountering birthday buddies", it's *much* easier to work out the probability of *not* encountering them.
Charlie Munger's "Invert, Always Invert" mantra comes in handy when analyzing the birthday paradox.
Instead of asking "what's the probability of encountering birthday buddies", it's *much* easier to work out the probability of *not* encountering them.
12/
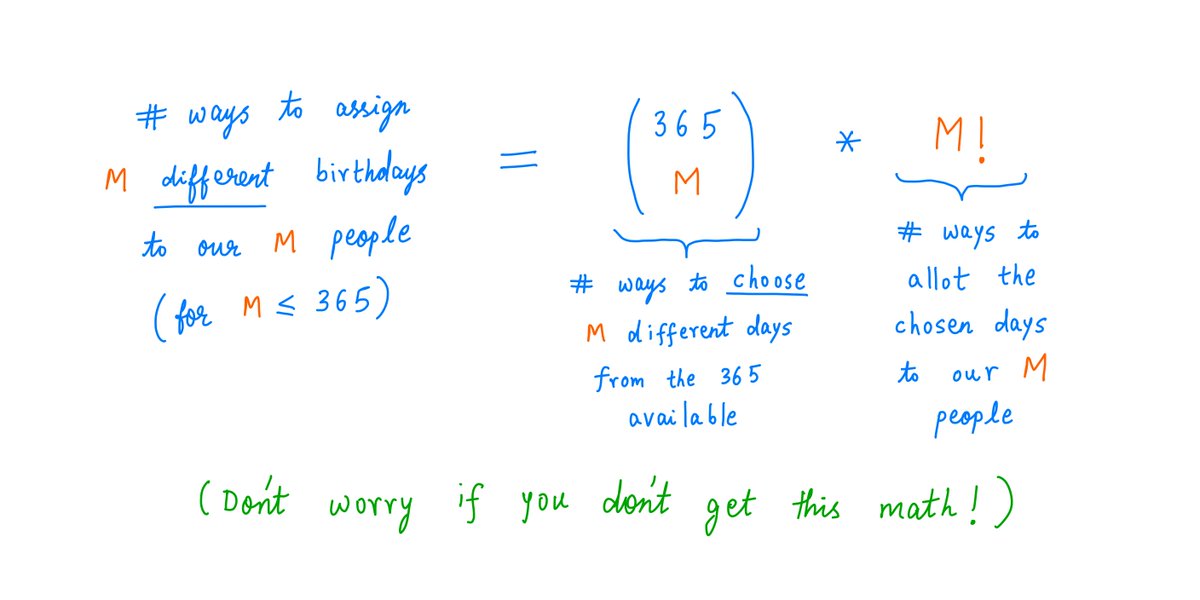
It's quite simple. If we *don't* want birthday buddies, we have to hope that *all* M people on our list have different birthdays.
This is like rolling a 365-sided die M times, and getting a different number each time.
Here's the number of ways that can happen:
It's quite simple. If we *don't* want birthday buddies, we have to hope that *all* M people on our list have different birthdays.
This is like rolling a 365-sided die M times, and getting a different number each time.
Here's the number of ways that can happen:
14/
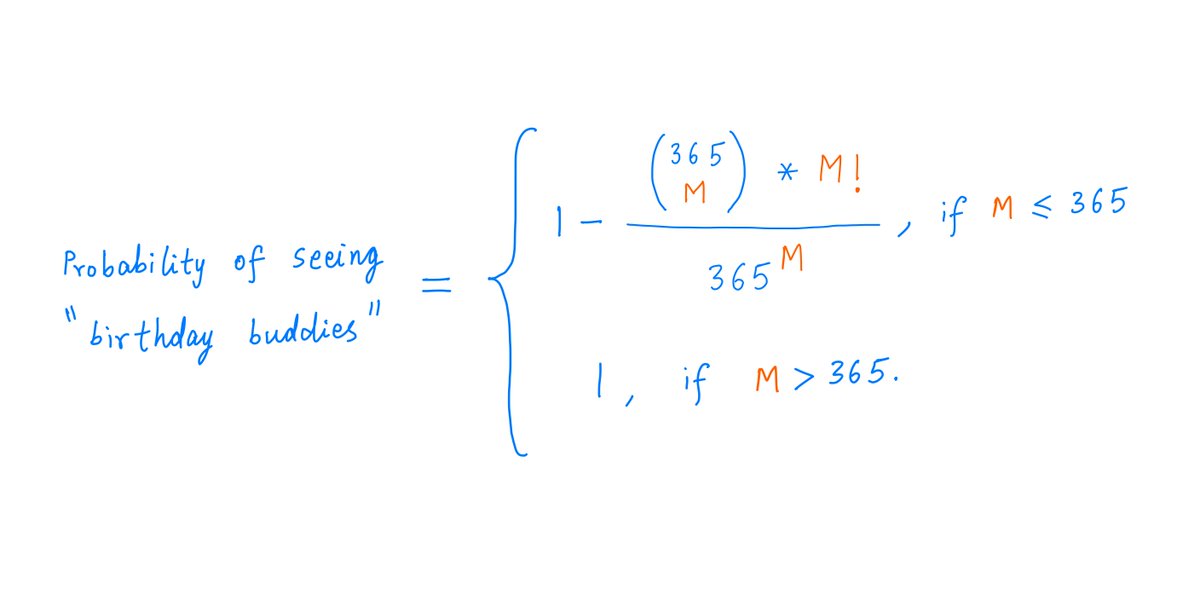
Since all these ways are equally likely, we can just divide one by the other to get the probability of *not* seeing birthday buddies:
Since all these ways are equally likely, we can just divide one by the other to get the probability of *not* seeing birthday buddies:
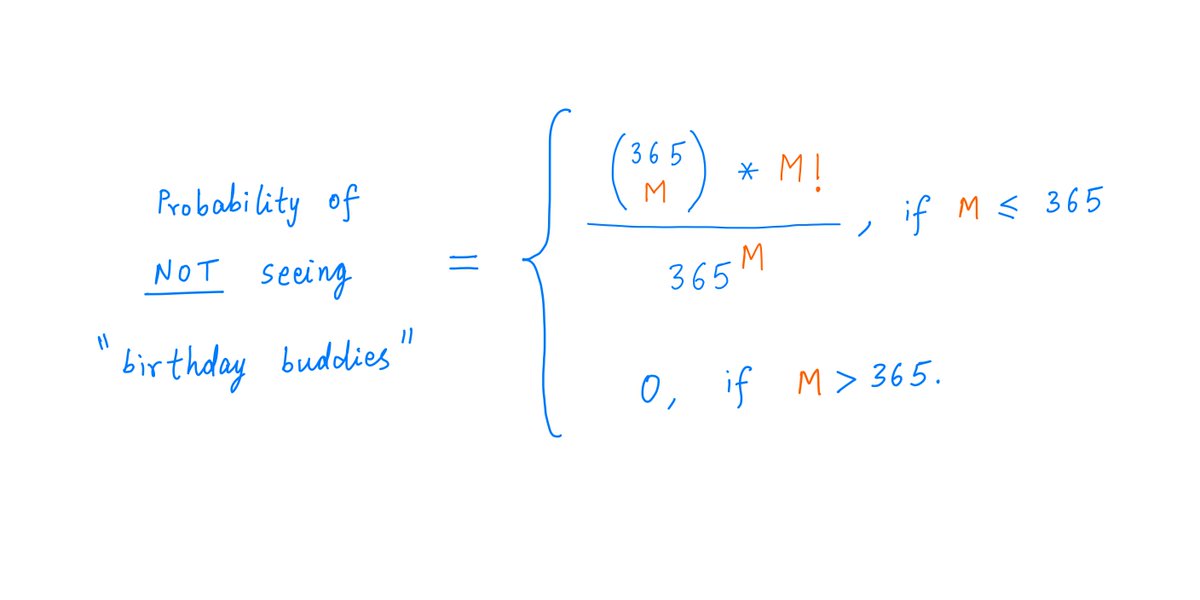
16/
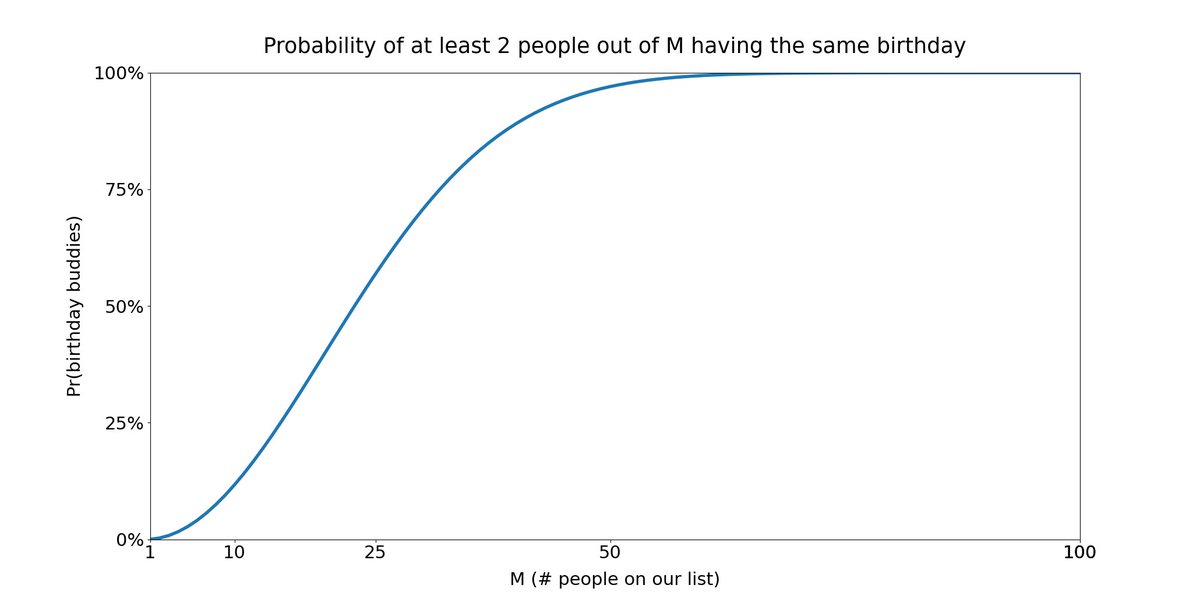
With this formula, we can plot the probability of seeing birthday buddies vs M.
From the plot, we see that as M increases, birthday buddies *rapidly* become more and more likely.
Linear thinking grossly *underestimates* this rapidity.
With this formula, we can plot the probability of seeing birthday buddies vs M.
From the plot, we see that as M increases, birthday buddies *rapidly* become more and more likely.
Linear thinking grossly *underestimates* this rapidity.
17/
To give you an idea of this rapidity:
At M = 23, the probability of seeing birthday buddies crosses the 50% mark.
At M = 32, the 75% mark.
At M = 41, the 90% mark.
And at M = 57, the 99% mark.
To give you an idea of this rapidity:
At M = 23, the probability of seeing birthday buddies crosses the 50% mark.
At M = 32, the 75% mark.
At M = 41, the 90% mark.
And at M = 57, the 99% mark.
18/
We also gain insight by looking at the *incremental* contribution of each increase in M.
For example, when M = 10, the probability of birthday buddies is about ~11.69%. At M = 11, it's ~14.11%.
So, the 11'th person's *incremental* contribution is 14.11 - 11.69 = ~2.42%.
We also gain insight by looking at the *incremental* contribution of each increase in M.
For example, when M = 10, the probability of birthday buddies is about ~11.69%. At M = 11, it's ~14.11%.
So, the 11'th person's *incremental* contribution is 14.11 - 11.69 = ~2.42%.
19/
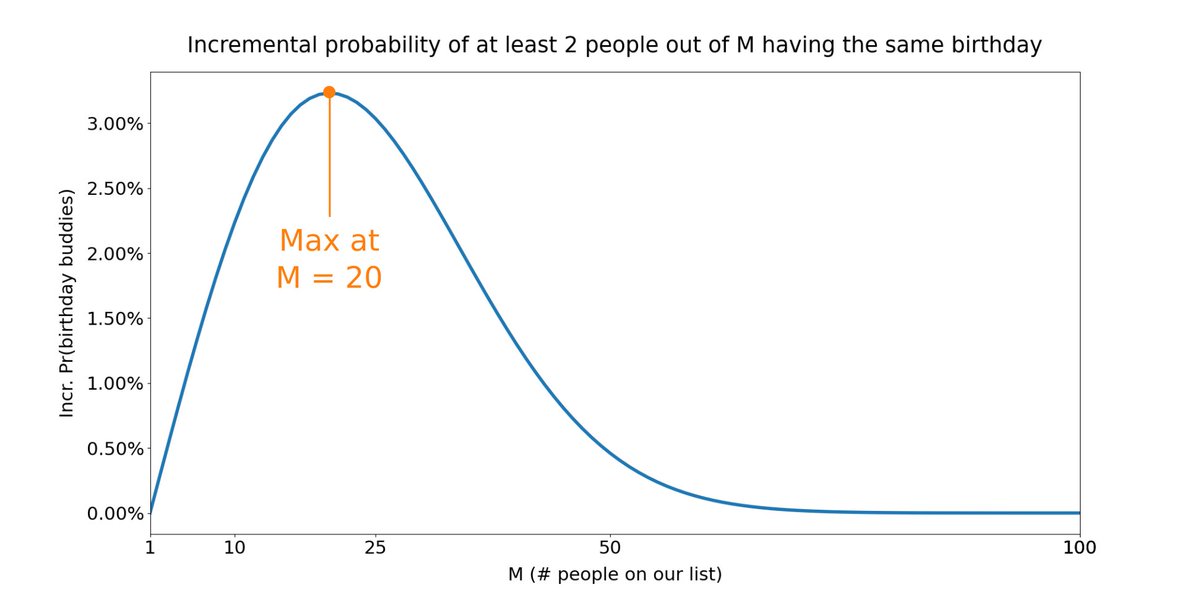
Here's a plot of these *incremental* contributions vs M.
This plot is very interesting.
It shows that initially, there's a *law of increasing returns*: each increment to M produces progressively *bigger* increments to birthday buddy likelihood.
Here's a plot of these *incremental* contributions vs M.
This plot is very interesting.
It shows that initially, there's a *law of increasing returns*: each increment to M produces progressively *bigger* increments to birthday buddy likelihood.
20/
But then, at around M = 20, this reverses course and becomes a *law of diminishing returns* instead.
Now, each increment to M produces progressively *smaller* increments to birthday buddy likelihood.
But then, at around M = 20, this reverses course and becomes a *law of diminishing returns* instead.
Now, each increment to M produces progressively *smaller* increments to birthday buddy likelihood.
21/
In other words, up to M = 20, each person contributes *more* than the previous one.
But starting at M = 21, each person contributes *less*.
The 20'th person contributes more than the 19'th. But the 21'st person contributes less than the 20'th.
In other words, up to M = 20, each person contributes *more* than the previous one.
But starting at M = 21, each person contributes *less*.
The 20'th person contributes more than the 19'th. But the 21'st person contributes less than the 20'th.
22/
This kind of "increasing returns up to a point, followed by diminishing returns after that point", is a common feature we see in many life situations.
It applies to learning new subjects. Building muscle. Returns on invested capital in many businesses.
This kind of "increasing returns up to a point, followed by diminishing returns after that point", is a common feature we see in many life situations.
It applies to learning new subjects. Building muscle. Returns on invested capital in many businesses.
23/
These situations are characterized by an "S curve".
Every S curve has an *inflection point*. This is where it transitions from increasing to diminishing returns. In our birthday paradox, this is M = 20.
When we see an S curve, it usually pays to think *non-linearly*.
These situations are characterized by an "S curve".
Every S curve has an *inflection point*. This is where it transitions from increasing to diminishing returns. In our birthday paradox, this is M = 20.
When we see an S curve, it usually pays to think *non-linearly*.
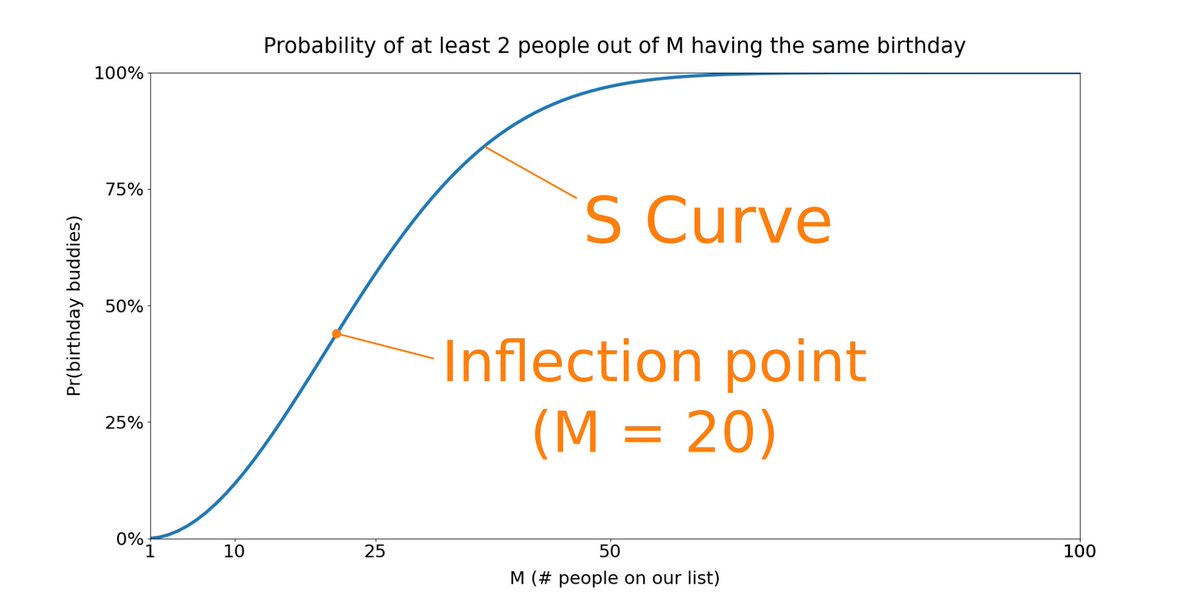
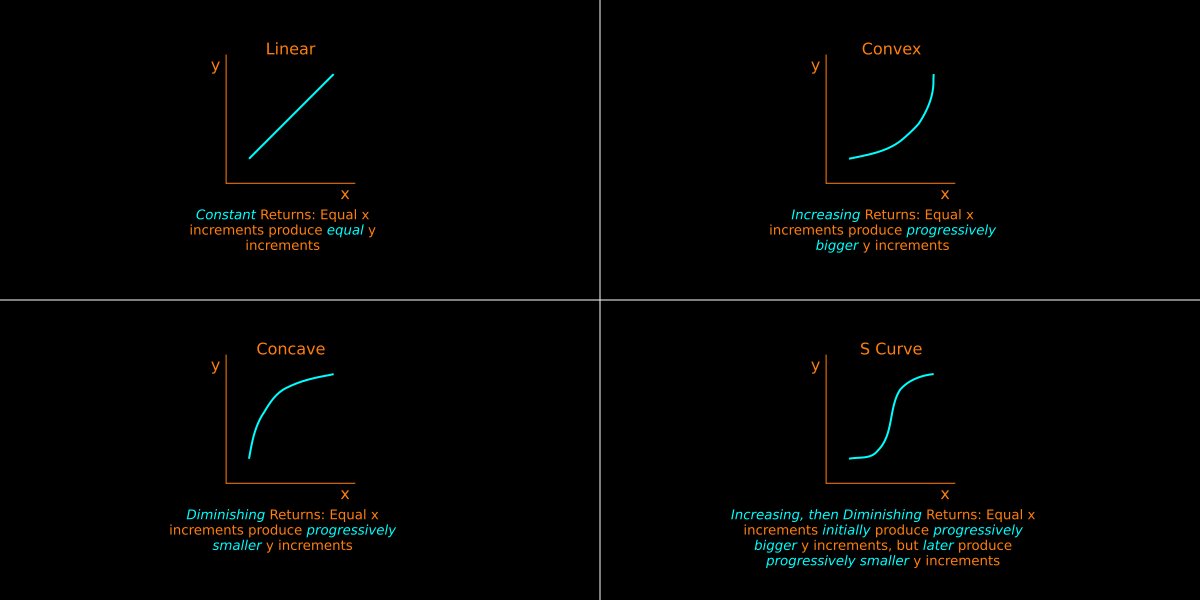
24/
Here's a picture to help you think non-linearly.
As the picture shows, the key idea is to think in terms of *incremental* returns: are they increasing (convex), diminishing (concave), constant (linear), or at first increasing but later on diminishing (S curve)?
Here's a picture to help you think non-linearly.
As the picture shows, the key idea is to think in terms of *incremental* returns: are they increasing (convex), diminishing (concave), constant (linear), or at first increasing but later on diminishing (S curve)?
25/
There are at least 5 key lessons we can learn from the birthday paradox.
Key lesson 1: Simplify the problem to its essentials.
For example, we decided to ignore Feb 29 birthdays. This helped us get rid of many messy corner cases -- *without* causing us to lose any insight.
There are at least 5 key lessons we can learn from the birthday paradox.
Key lesson 1: Simplify the problem to its essentials.
For example, we decided to ignore Feb 29 birthdays. This helped us get rid of many messy corner cases -- *without* causing us to lose any insight.
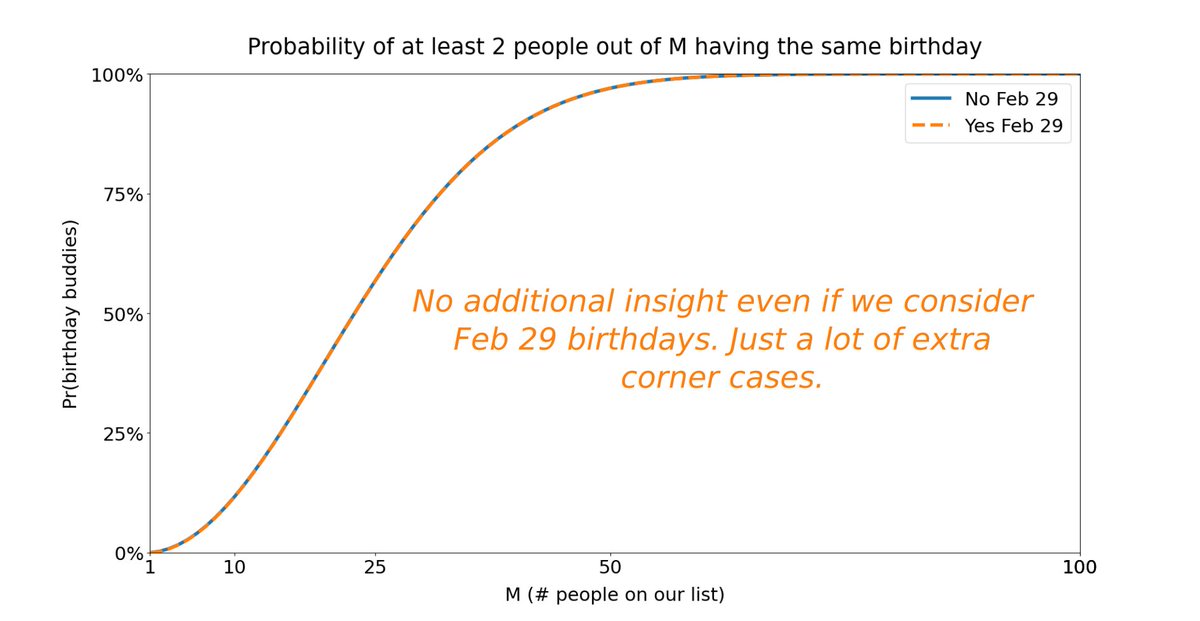
26/
Key lesson 2: Don't over-simplify.
Linear thinking is an example of over-simplification in this case. It causes us to dramatically underestimate the likelihood of seeing birthday buddies -- and thereby miss crucial insights.
Key lesson 2: Don't over-simplify.
Linear thinking is an example of over-simplification in this case. It causes us to dramatically underestimate the likelihood of seeing birthday buddies -- and thereby miss crucial insights.
27/
Key lesson 3: Think probabilistically.
Most outcomes in life are not deterministic. Chance often plays a big role.
So, it's usually a good idea to enumerate the various possible outcomes, work out which ones are desirable and undesirable, the odds of each, etc.
Key lesson 3: Think probabilistically.
Most outcomes in life are not deterministic. Chance often plays a big role.
So, it's usually a good idea to enumerate the various possible outcomes, work out which ones are desirable and undesirable, the odds of each, etc.
28/
Key lesson 4: Invert, always invert.
In many probabilistic situations, inverting the problem (eg, asking how many ways birthday buddies *cannot* occur) can help us solve it.
As Charlie Munger is fond of saying: I only want to know where I'll die, so I'll never go there.
Key lesson 4: Invert, always invert.
In many probabilistic situations, inverting the problem (eg, asking how many ways birthday buddies *cannot* occur) can help us solve it.
As Charlie Munger is fond of saying: I only want to know where I'll die, so I'll never go there.
29/
Key lesson 5: Think non-linearly.
This often means thinking in terms of *incremental* or *marginal* returns.
For this, it's useful to bear in mind mental models like convexity, concavity, S curves, inflection points, etc.
Key lesson 5: Think non-linearly.
This often means thinking in terms of *incremental* or *marginal* returns.
For this, it's useful to bear in mind mental models like convexity, concavity, S curves, inflection points, etc.
30/
As usual, I'll leave you with some useful references.
I love Shannon's 1952 speech outlining 6 methods for thinking creatively and solving problems strategically. Two of the methods are "simplifying" and "inverting". (h/t @jimmyasoni)
For more:
As usual, I'll leave you with some useful references.
I love Shannon's 1952 speech outlining 6 methods for thinking creatively and solving problems strategically. Two of the methods are "simplifying" and "inverting". (h/t @jimmyasoni)
For more:
https://twitter.com/10kdiver/status/1260191715954049024?s=20
31/
I also recommend listening to this (~1 hr, 23 min) podcast episode, where @ShaneAParrish and @Scott_E_Page discuss several mental models for both non-linear and probabilistic thinking -- including convexity and concavity, Markov chains, etc. fs.blog/knowledge-proj…
I also recommend listening to this (~1 hr, 23 min) podcast episode, where @ShaneAParrish and @Scott_E_Page discuss several mental models for both non-linear and probabilistic thinking -- including convexity and concavity, Markov chains, etc. fs.blog/knowledge-proj…
32/
Also, this article by @eugenewei on how to anticipate inflection points in S curves (he calls them invisible asymptotes) is excellent: eugenewei.com/blog/2018/5/21…
Also, this article by @eugenewei on how to anticipate inflection points in S curves (he calls them invisible asymptotes) is excellent: eugenewei.com/blog/2018/5/21…
33/
Finally, I want to thank my friend @SahilBloom.
It was his 30'th birthday earlier this week (and @aryamanar99's suggestion that I "gift" him a thread) that prompted me to reflect on birthdays and the birthday paradox.
Happy birthday, Sahil!
Finally, I want to thank my friend @SahilBloom.
It was his 30'th birthday earlier this week (and @aryamanar99's suggestion that I "gift" him a thread) that prompted me to reflect on birthdays and the birthday paradox.
Happy birthday, Sahil!
34/
If you're still with me, kudos to your perseverance!
Forget *non-linear* thinking. Most people can't follow a thread linearly from start to finish. But you're not one of them, and I appreciate it!
Take care. Enjoy your weekend!
/End
If you're still with me, kudos to your perseverance!
Forget *non-linear* thinking. Most people can't follow a thread linearly from start to finish. But you're not one of them, and I appreciate it!
Take care. Enjoy your weekend!
/End
• • •
Missing some Tweet in this thread? You can try to
force a refresh