how do you calculate correct normals when doing vertex displacement shaders?
here's a lil guide/example on the overly complicated but mathematically correct way of doing this~
here's a lil guide/example on the overly complicated but mathematically correct way of doing this~

say you have this simple smoothstep bump, with a radius (r) and an amplitude (a)
the space we're working in will be in uv space, where (0,0) is in the center of this plane
o.uv = the current 2d uv coordinate
d = length(o.uv)
height = smoothstep(r,0,d)*a;
the space we're working in will be in uv space, where (0,0) is in the center of this plane
o.uv = the current 2d uv coordinate
d = length(o.uv)
height = smoothstep(r,0,d)*a;
what we need is called the partial derivatives (rate of change) of this function, in order to calculate the normal
now, we're going the unnecessarily accurate route, so we're not using the ddx/ddy functions in the frag shader, that's cheating~
now, we're going the unnecessarily accurate route, so we're not using the ddx/ddy functions in the frag shader, that's cheating~
in order to do this, we have to unpack the math a little so we can differentiate it, so, let's do that!
first off, smoothstep(a,b,v) is a (clamped) inverse lerp:
t = saturate((v-a)/(b-a))
...followed by a cubic smooth function:
t²(3-2t)
source: developer.download.nvidia.com/cg/smoothstep.…
first off, smoothstep(a,b,v) is a (clamped) inverse lerp:
t = saturate((v-a)/(b-a))
...followed by a cubic smooth function:
t²(3-2t)
source: developer.download.nvidia.com/cg/smoothstep.…

the point of inverse lerp here is to remap the distance d from 0 to r into 1 to 0
(1 in the center, 0 at radius distance away from the center)
simplifying:
t = invLerp( r, 0, d ) =
(d-r)/(0-r) =
1-d/r
so, now that we know t = 1-d/r, let's apply the cubic smooth function
(1 in the center, 0 at radius distance away from the center)
simplifying:
t = invLerp( r, 0, d ) =
(d-r)/(0-r) =
1-d/r
so, now that we know t = 1-d/r, let's apply the cubic smooth function
now, working out this math is tedious and boring so let's throw what we've got into wolfram alpha:
t²(3-2t) where t = 1-d/r
and, we get a nice formula back! thx wolfie~
t²(3-2t) where t = 1-d/r
and, we get a nice formula back! thx wolfie~

finally, we need to scale it by the amplitude with a simple multiply, and we end up with:
height = (a(d-r)²(2d+r))/r³
beautiful! however, we forgot the clamp~
in code we can just clamp d to never be greater than r:
d = min( length(o.uv), r )
height = (a(d-r)²(2d+r))/r³
beautiful! however, we forgot the clamp~
in code we can just clamp d to never be greater than r:
d = min( length(o.uv), r )
now, it's a little hidden in the formula, but we actually have *two* inputs to this function, not one
d = length(o.uv) is kinda hiding that it's based on u and v, so let's be even more verbose:
d = length(o.uv) = √(u²+v²)
d = length(o.uv) is kinda hiding that it's based on u and v, so let's be even more verbose:
d = length(o.uv) = √(u²+v²)
so what did we just do?
instead of:
d = length(o.uv)
height = smoothstep(r,0,d)*a;
we now have:
height = (a(√(u²+v²)-r)²(2√(u²+v²)+r))/r³
wow this looks much less clean, thanks math!
however, with math, we can do some magic~
instead of:
d = length(o.uv)
height = smoothstep(r,0,d)*a;
we now have:
height = (a(√(u²+v²)-r)²(2√(u²+v²)+r))/r³
wow this looks much less clean, thanks math!
however, with math, we can do some magic~
we need to know - what is the rate of change (derivative) of this formula, along u and v, respectively?
well, we just throw this to the wolves again to get the partial derivatives:
f(u,v) = (a(√(u²+v²)-r)²(2√(u²+v²)+r))/r³
and wolfie gives us exactly what we need~
well, we just throw this to the wolves again to get the partial derivatives:
f(u,v) = (a(√(u²+v²)-r)²(2√(u²+v²)+r))/r³
and wolfie gives us exactly what we need~
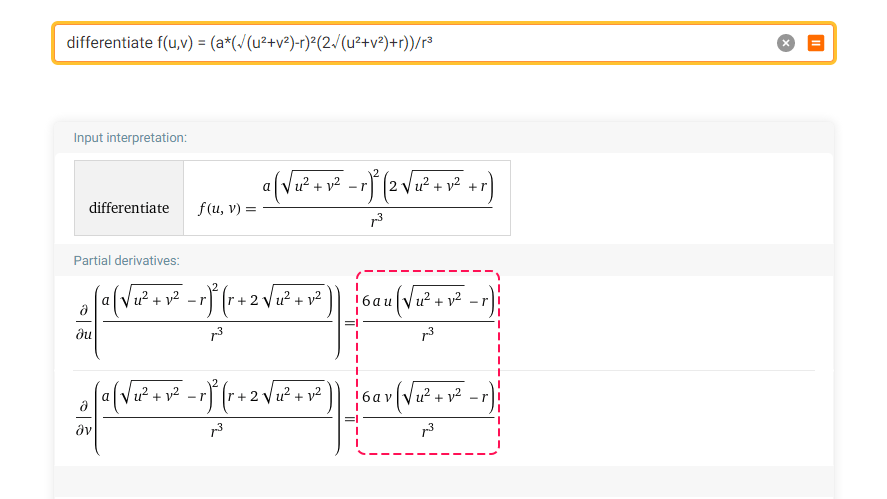
∂f/∂u = 6au(√(u²+v²)-r)/r³
∂f/∂v = 6av(√(u²+v²)-r)/r³
we can write this in one line as a vector in shader code, since there's only one place they differ!
pd = 6a*o.uv*(√(u²+v²)-r)/r³
we can also simplify since √(u²+v²) = d:
pd = 6a*o.uv*(d-r)/r³
∂f/∂v = 6av(√(u²+v²)-r)/r³
we can write this in one line as a vector in shader code, since there's only one place they differ!
pd = 6a*o.uv*(√(u²+v²)-r)/r³
we can also simplify since √(u²+v²) = d:
pd = 6a*o.uv*(d-r)/r³
so what we have now, is the *slope* of this surface, along u and v, but we don't have the normal
now, whenever you want to convert from a slope to a vector, you insert the slope as components, while the remaining components equal 1
normal = normalize(float3(pd.x, pd.y, 1))
now, whenever you want to convert from a slope to a vector, you insert the slope as components, while the remaining components equal 1
normal = normalize(float3(pd.x, pd.y, 1))
that's it! hell yea normals 💜
d = min( length(o.uv), r )
h = (a(d-r)²(2d+r))/r³
pd = 6a*o.uv*(d-r)/r³
normal = normalize(float3(pd,1))
d = min( length(o.uv), r )
h = (a(d-r)²(2d+r))/r³
pd = 6a*o.uv*(d-r)/r³
normal = normalize(float3(pd,1))

also, here's an interactive version of this hump (in 2D instead of 3D) if you want to play with sliders 📈
desmos.com/calculator/aoq…
desmos.com/calculator/aoq…
~FAQ~
Q: isn't it easier to just-
A: yes! this is the long way around. very slow to work with as you need to redo the math for every new input, but it's accurate as heck/not an approximation~
Q: what if my shape isn't a plane
A: transform this from tangent space or something idk
Q: isn't it easier to just-
A: yes! this is the long way around. very slow to work with as you need to redo the math for every new input, but it's accurate as heck/not an approximation~
Q: what if my shape isn't a plane
A: transform this from tangent space or something idk
• • •
Missing some Tweet in this thread? You can try to
force a refresh


![an image of pixel digits, along with code that reads: static uint dBits[5] = { 3959160828, 2828738996, 2881485308, 2853333412, 3958634981 }; float DrawDigit(int2 px, const int digit){ if (px.x < 0 || px.x > 2 || px.y < 0 || px.y > 4) return 0; // pixel out of bounds const int xId = (digit == -1) ? 18 : 31 - (3 * digit + px.x); return (dBits[px.y] & 1 << xId) != 0; }](https://pbs.twimg.com/media/GUtaRtMWwAIz97a.png)




