Share this page!

Enter URL or ID to Unroll

You can paste full URL like: https://x.com/threadreaderapp/status/1644127596119195649
or just the ID like: 1644127596119195649

How to get URL link on X (Twitter) App

  1. On the Twitter thread, click on or icon on the bottom
  2. Click again on or Share Via icon
  3. Click on Copy Link to Tweet
  4. Paste it above and click "Unroll Thread"!
  5. More info at Twitter Help
Eric Lengyel Profile picture
@EricLengyel
Apr 21, 2021 • 1 tweets • 1 min read • Read on X
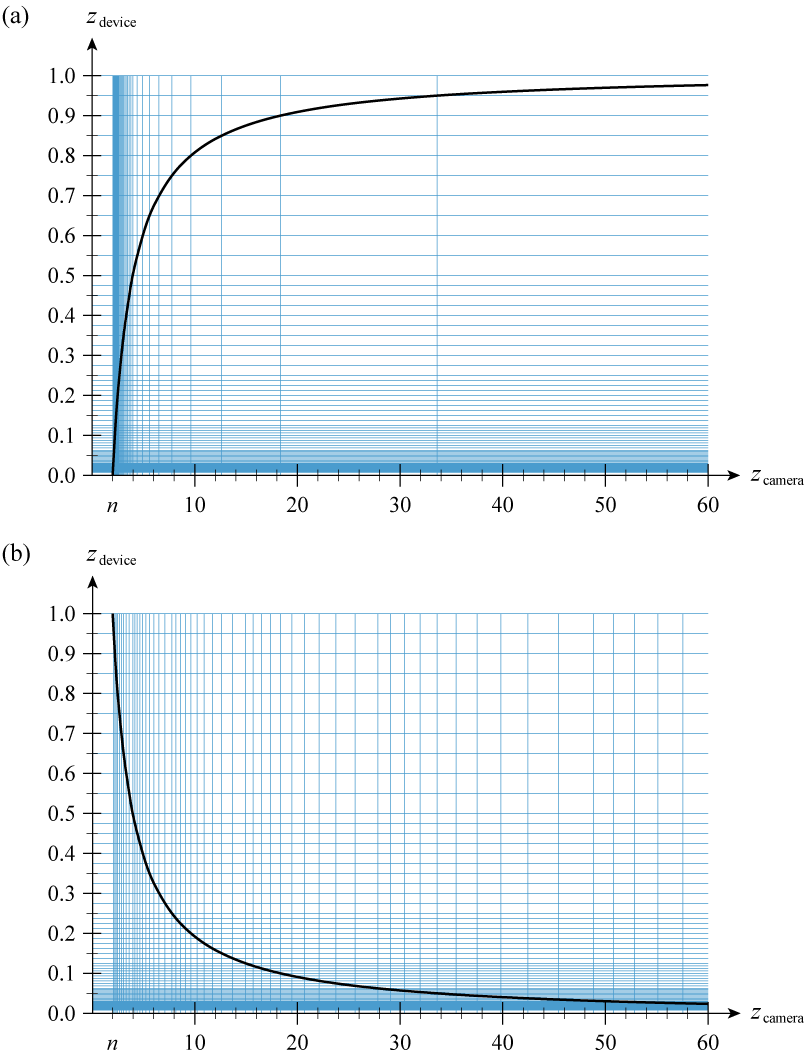
@m_schuetz @CianNoonan The superior distribution is demonstrated by the vertical lines in this diagram from Foundations of Game Engine Development, Vol. 2. (a) Depth is mapped from 0 to 1. (b) Depth is mapped from 1 to 0. amazon.com/dp/0985811757/… Image

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Eric Lengyel

Eric Lengyel Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @EricLengyel

Eric Lengyel Profile picture
Oct 26, 2022
So why intrusive containers in C4? To look at one example out of many, consider that a single node in the scene can range in size from a few hundred bytes to roughly a kilobyte in size. (The largest levels I've worked with have more than a million nodes in them.) 1/9
Every node is part of a big transform tree. Instanced objects are attached to the main world somewhere, and they may contain other instanced objects. Character models typically have a node hierarchy (like a skeleton for skinning) that can be ~dozen nodes deep. 2/9
Nodes often have ancillary components attached to them like properties and a controller. Nodes can be added to or removed from the transform tree at any time. They may even move to a different location in the tree when, for example, a character picks something up. 3/9
Read 9 tweets
Eric Lengyel Profile picture
Oct 26, 2022
The largest task remaining before I can release C4 Engine version 7.0 is an upgrade to the GI solution. For many years, the engine has been using a volumetric "illuminance space" that contains precomputed ambient light for 6 directions at every point inside a 3D grid. 1/12
To fit the data into 8 channels over two 3D textures (in RGBA8 format), 6 intensities are stored for each sample point, but only one two-component color value is stored. This has the undesirable effect of making the sky color or ground color bleed into other directions. 2/12
In large outdoor areas, there is also the limitation that you need to use one extra-large volume to cover everything, and it only gives you a single uniform sampling resolution. We need more detail where structures are sitting on the terrain, for example. 3/12
Read 12 tweets
Eric Lengyel Profile picture
Jan 19, 2022
The 8 basis elements for the 3D geometric algebra correspond to the 8 ways that three dimensions x, y, and z can be partitioned into two groups, shown as red and blue here. The symmetries of duality arise from an operation that simply swaps the two colors. Image
Quaternions are multivectors only with components having an even number of red dimensions, and they look like this. Quaternions perform rotations, and they correspond to all possible proper isometries in 3D space that leave the origin fixed. Image
What about the basis elements with an odd number of red dimensions? They look like this, and they perform *rotoreflections*. These correspond to all possible improper isometries in 3D space that leave the origin fixed. Image
Read 4 tweets
Eric Lengyel Profile picture
May 3, 2021
Back in 1993, I was taking a number theory class, and there was a semester-long factorization contest that we could participate in. I implemented a distributed multiple polynomial quadratic sieve (MPQS) for the Mac, and I needed a cluster of computers to run it on.
The computer lab in the math building had a bunch of Mac Centris 650s on an AppleTalk network. But they were running some kind of secure software that didn't give you access to the Finder, only specific software, so I couldn't pop in a disk and run my own programs.
You can see in this picture that the Centris had two little buttons on the front. One was a reset button, and the other generated a non-maskable interrupt (NMI). If Macsbug was installed, the NMI button froze everything and dropped you into the system debugger.
Read 9 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us!

Send Email!

:(