Thread by @ValeriiZhyla

Много лет назад один профессор показал нам отличный метод умножения матриц, и я решил о нём рассказать

В процессе учебы мне приходилось вручную умножать тысячи матриц, разной размерности и сложности. Классический перебор "строчка на столбик" имеет колоссальную когнитивную нагрузку, а поиск ошибки в нем – зачастую провальное мероприятие

Итак, коротко рассмотрим классический метод на умножении двух квадратных матриц 3х3

Выбираем строчку и столбик, и умножаем по очереди каждый элемент строки на соответствующий элемент столбика, сумму этих произведений записываем, это результат умножения строки первой матрицы на столбик второй

Красный на синий: 2*5 + 6*1 + 1*9 = 25, 25 записываем

Вдруг мы задумались, или устали от десяти предыдущих матриц, и посчитали строку с неправильным столбиком. Такие ситуации, по крайней мере у меня, происходят постоянно, когда решать нужно быстро.

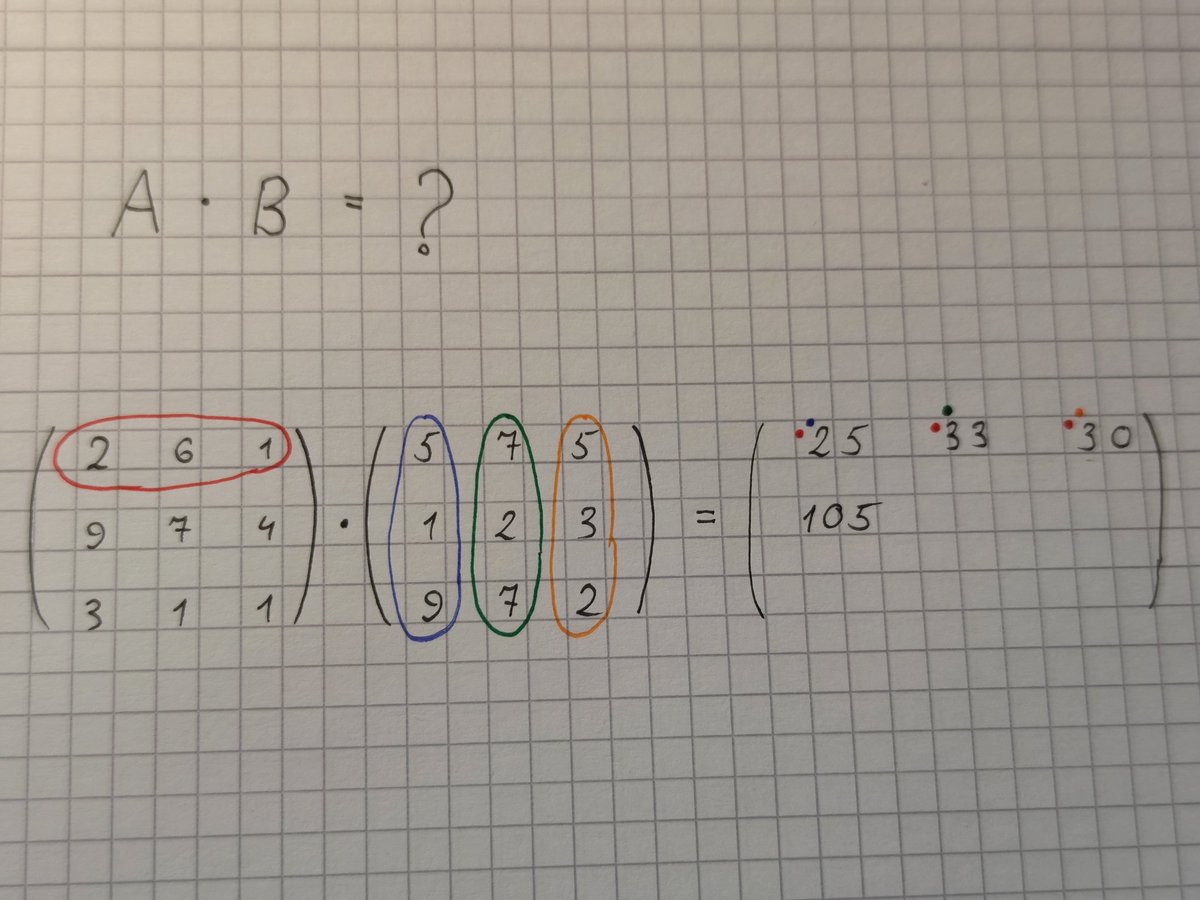
Ошибку можно заметить и исправить, но ясно одно: этот метод жрет больше сил на обдумывание, что на что умножать, чем на непосредственный расчет. Очень неэффективно. Особенно если матрицы разного размера.

На свалку этот способ!

Критикуешь – предлагай.
Если мы хотим найти A * B, то это можно сделать вот такой вот лесенкой. В этом примере я её рисую карандашом и цветами, но обычно всё делается просто по клеткам

Нужно произвести ровно те же самые вычисления, но теперь не нужно думать, что с чем умножать. Результат считается в местах пересечения строки и столбика

Считаем первый элемент. Арифметика та же самая, а когнитивная нагрузка испарилась, или по крайней мере, очень сильно уменьшилась

И вот, мы получили результат. Возможно, мы готовы. А если нужно его дальше использовать в умножении? Этот способ как раз на это и рассчитан!

Например, мы хотим умножить наш результат A*B справа на матрицу С. Отлично, дописываем её справа и считаем пересечения

И на пересечениях будет содержаться матрица (A*B)*C

Хорошо, справа умножить можно, а слева?

Пожалуйста!
Наше дерево просто растет вниз в нужном месте. Посчитаем пересечения, и получим результат D * (A*B)

Вот так вот, довольно интуитивно

У этого метода есть ещё один огромный козырь. Он позволяет умножать матрицы разной размерности, вообще не задумываясь о том, в какой форме должен быть результат. Структура сетки сама задаст размерность результата.

Попробуем умножить две прямоугольные матрицы разного размера. Синюю на красную, 6x2 на 2х3.

Сетка решения позволяет нам не задумываться о том, совместимы ли матрицы, и какой формы будет результат. В данном случае сразу видно, что результат имеет форму 6х3.

Конечно, опытный человек формы видит сразу, и знает, как их считать, это же проще простого. Но у первокурсников вечно с этим проблемы.

Хорошо, но этот метод выглядит так громоздко!
На самом деле, нет. Я нарисовал всё в цветах и кучей места для наглядности, а в реальности, при простых расчетах, всё выглядит так:

Или даже так:

Когда привыкаешь так считать, вспомогательные линии становятся не нужны.

Если же матрицы сложные, или числа побольше, то в любом случае имеет смысл не экономить место. Бумага дешёвая, баллы и нервы – бесценны.

Если же мы считаем произведения матриц, состоящих не из чисел, а из функций, то оставлять в любом случае нужно столько свободного места, сколько возможно.

Вот такая вот история получилась!
Надеюсь, кому-нибудь будет полезно)
@threadreaderapp unroll