
Last week I did the Sylow theorems in class, and I want to share how I do them with my visual approach to groups.
To start, here are the 5 groups of order 12. Note how there are "towers of p-groups", for p=2 and p=3.
This is what the 1st Sylow theorem guarantees.
1/17

To start, here are the 5 groups of order 12. Note how there are "towers of p-groups", for p=2 and p=3.
This is what the 1st Sylow theorem guarantees.
1/17


The key lemma needed for the Sylow theorems is:
"If a p-group G acts on S, then |Fix|≡|S| mod p."
Here's a picture proof of that, adapted from @nathancarter5's fantastic "Visual Group Theory" book.
2/17
"If a p-group G acts on S, then |Fix|≡|S| mod p."
Here's a picture proof of that, adapted from @nathancarter5's fantastic "Visual Group Theory" book.
2/17

As a corollary of this, by letting a p-group act on its subgroups by conjugation:
"p-groups cannot have fully unnormal subgroups"
Said differently, the normalizer of any subgroup strictly gets bigger. Here's what I mean by that concept.
3/17

"p-groups cannot have fully unnormal subgroups"
Said differently, the normalizer of any subgroup strictly gets bigger. Here's what I mean by that concept.
3/17


Here are two pictures for why that's true for subgroups of p-groups, which is a direct application of: "If a p-group G acts on S, then |Fix|≡|S| mod p."
I describe the 2nd picture as:
"# blue marbles mod p = total # marbles mod p"
4/17

I describe the 2nd picture as:
"# blue marbles mod p = total # marbles mod p"
4/17


It's straightforward to extend this to non-Sylow p-subgroups of arbitrary finite groups.
Here's a picture of that. Note that a "non-Sylow p-subgroup" just means a non-maximal p-subgroup.
5/17
Here's a picture of that. Note that a "non-Sylow p-subgroup" just means a non-maximal p-subgroup.
5/17

Before we begin the Sylow theorems, let's consider a "mystery group" of order 12, and see how much we can uncover about its structure.
6/17
6/17

The first Sylow theorem simply says that for any prime p dividing |G|, there is a "complete saturated p-subgroup tower" in the subgroup lattice, like in the 1st picture of this thread.
Tip: throughout, picture chains of p-subgroups rising vertically, not horizontally.
7/17
Tip: throughout, picture chains of p-subgroups rising vertically, not horizontally.
7/17
The proof is by induction. Given a non-Sylow p-subgroup H of order p^k, consider the (non-trivial) p-group N_G(H)/H, and find an element (coset!) of order p.
The union of those cosets is a subgroup of order p^{k+1}.
Here's a visual, also adapted from @nathancarter5's VGT.
8/17
The union of those cosets is a subgroup of order p^{k+1}.
Here's a visual, also adapted from @nathancarter5's VGT.
8/17

The 2nd Sylow theorem says that all subgroups at the top of the p-subgroup tower are conjugate. Note how I denoted this with dashed lines.
In particular, the following situation is impossible.
10/17
In particular, the following situation is impossible.
10/17

I actually prove a stronger version -- the "strong 2nd Sylow theorem":
If H is p-Sylow, then every p-subgroup is conjugate to some subgroup of H. This is best seen by a picture.
The only question is: "how to we find such an element g"?
11/17
If H is p-Sylow, then every p-subgroup is conjugate to some subgroup of H. This is best seen by a picture.
The only question is: "how to we find such an element g"?
11/17

We let some other Sylow p-subgroup H' act on the cosets of H.
Any element g such that Hg is a fixed point will work!
So why *is* there a fixed point? |S|=[G:H] is not a multiple of p, and we immediately get |Fix|≡|S| mod p ≠ 0. Done!
12/17
Any element g such that Hg is a fixed point will work!
So why *is* there a fixed point? |S|=[G:H] is not a multiple of p, and we immediately get |Fix|≡|S| mod p ≠ 0. Done!
12/17

Let's do a quick corollary. Given only the subgroup lattice for A_5, we can see by inspection why it's simple.
Can you fill in the details? Notice that the conjugacy classes of the Sylow p-subgroups are dashed.
13/17
Can you fill in the details? Notice that the conjugacy classes of the Sylow p-subgroups are dashed.
13/17

Notice how in A_5, if you take the normalizer of a p-subgroup, you "go up", but if you do it again, you stay put.
This is nicely characterized by the terminology of "moderately unnormal" and "fully unnormal" that I introduced earlier.
14/17
This is nicely characterized by the terminology of "moderately unnormal" and "fully unnormal" that I introduced earlier.
14/17

Finally, the 3rd Sylow theorem: the number of Sylow p-subgroups n_p, satisfies:
(1) n_p | m
(2) n_p ≡ 1 mod p
For (1), let G act on Syl(G) by conjugation. There's 1 orbit, so the result is immediate by the orbit-stabilizer theorem: n_p = |orb(H)| = [G:stab(H)].
15/17
(1) n_p | m
(2) n_p ≡ 1 mod p
For (1), let G act on Syl(G) by conjugation. There's 1 orbit, so the result is immediate by the orbit-stabilizer theorem: n_p = |orb(H)| = [G:stab(H)].
15/17
For (2), let a Sylow p-subgroup P act on Syl(G), and show that the only fixed point is P. The result now follows from our "fixed point lemma":
1 = |Fix| ≡ n_p mod p.
16/17
1 = |Fix| ≡ n_p mod p.
16/17
Here's a final version of our "mystery group of order 12". From here, we're a few steps from formally classifying all 5 groups of order 12; here are the lattices again.
Tip: rely heavily on lattices when teaching Sylow theory. Draw the p-subgroup towers vertically!
17/17

Tip: rely heavily on lattices when teaching Sylow theory. Draw the p-subgroup towers vertically!
17/17


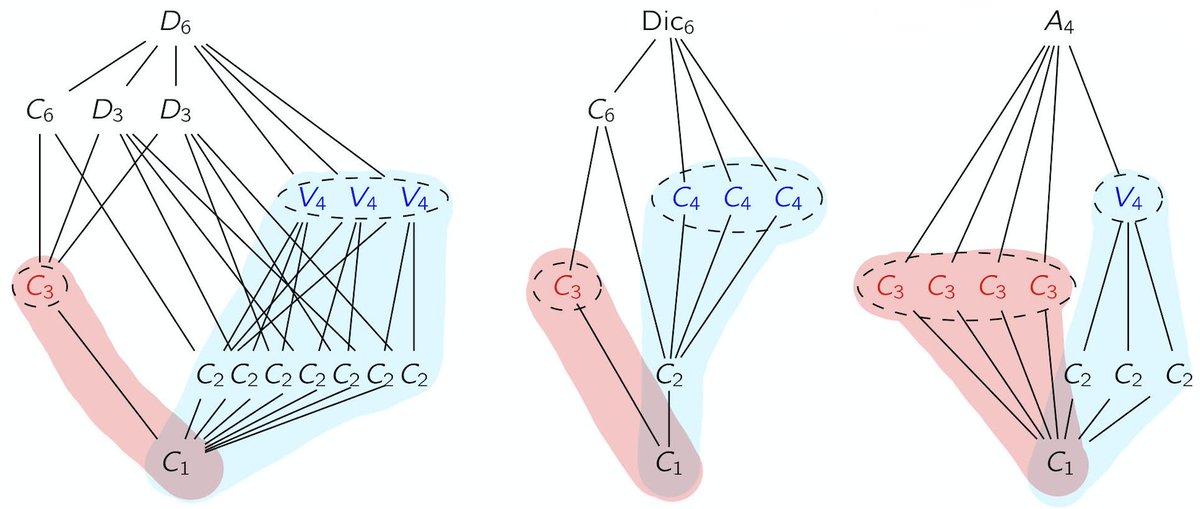
Oops, I only included the lattices of the two abelian groups of order 12 in that last tweet. Here are the 3 non-abelian ones:
1. the dihedral group D_6
2. the diciclic group Dic_6
3. the alternating group A_4
18/17
1. the dihedral group D_6
2. the diciclic group Dic_6
3. the alternating group A_4
18/17
***Correction on page 14/17:
“normalizer of a SYLOW p-subgroup”
“normalizer of a SYLOW p-subgroup”
• • •
Missing some Tweet in this thread? You can try to
force a refresh




