Thread by @ValeriiZhyla

Сегодня я расскажу простым языком про сложность алгоритмов и Big O Notation. Все основы теории алгоритмов в одном треде!

В этом треде мы поговорим об О Нотации и разберем её по кусочкам. После этого речь пойдет о псевдокоде, и с его помощью мы рассмотрим два простейших алгоритма из мира массивов - Linear Search и Binary Search. После этого мы продолжим погружение в мир алгоритмов!

Этот тред рассчитан на новичков в этой области, и я постараюсь изложить все идеи и концепции простым языком, но без ощутимой потери глубины.

- Классическое упоминание о том, что ретвиты моих тредов ускоряют падение тоталитарных режимов, появлению волос там, где они нужнее всего и защищают от переломов копчика в суровую зимнюю пору.

Отдельное спасибо @usehex за помощь в создании и редактировании треда!

Итак, получасовое вступление позади, приступаем к делу.

Big O Notation можно перевести на русский как Большая "О" Нотация, часто говорят просто - О-Нотация. Давайте сначала разберемся, что это такое и зачем это нужно.

Big O Notation - способ обозначения сложности алгоритма. Но что вообще значит "сложность" алгоритма?

Для любого алгоритмы различают обычно два вида характеристик - его "время" и "память".

"Время" - это буквально...время, которое нужно алгоритму для завершения обработки каких-то данных. Например, 10 секунд для маленького массива, 100 секунд для массива побольше. Интуитивно понятно, что в таком случае время выполнения зависит от размера массива.

Проблема: секунды, минуты, часы и т.д - довольно расплывчатая метрика. Она становится ещё хуже, когда мы вспоминаем, что время работы алгоритма часто зависит от железа, на котором оно выполняется, а так же находится под влиянием большого количества внешних факторов.

По этой причине время считают не во "времени по часам", а в количестве операций, которые алгоритм совершит. Это однозначно более надёжная, и, главное, более независимая от железа, метрика.

Когда мы говорим про Time Complexity, или просто Time, то речь идет как раз про время.
Разница в скорости между разными операциями обычно опускается, для практической пользы.

Хоть деление чисел с плавающей точкой точно и потребует больше операций процессора, чем сложение целых чисел, они рассматриваются в алгоритмах как две операции с одинаковой ценой.

Иначе вся теория алгоритмов скатилась бы в какой-то ад, запутавшись в соотношениях, пропорциях и так далее.

Так что на первых порах просто запомните:
одна операция с одной или двумя переменными = одна единица времени.

i++, a*b, a/1024, max(a,b) - четыре примера операций, требующих одну единицу времени в О Нотации.

"Память", она же "место" - объем дополнительной памяти, требующийся алгоритму для работы. Одна переменная - одна ячейка памяти. Массив с тысячей ячеек - тысяча ячеек памяти.

Все ячейки, как и в случае со временем, являются равноценными - int a (на 4 байта) и double b (на 8 байт) рассматриваются как равноценные единицы памяти. Потребление памяти обычно называется Space Complexity, или же просто Space, и очень редко - Memory.

Алгоритм, который не требует большого объема дополнительной памяти (например, создает только одиночные переменные, но не создает копий исходного массива или промежуточные структуры данных) называют in-place.

Такие алгоритмы часто используют исходный массив как рабочее пространство. Очень экономные и бережливые ребята!

Алгоритмы, требующие дополнительную память, называют out-of-place.

Но...зачем оно вообще нам нужно?

Если коротко: это проверенный временем и общепринятый способ характеризации и сравнения разных алгоритмов.

Способ этот довольно удобный и точный (с определенными проблемами в виде недооценивания констант, о котором мы обязательно поговорим).

Потребление бензина и мощность двигателя на тестовом стенде, если угодно.
Для двигателей же существуют тестовые стенды? Уверен в этом. Но в машинах я не разбираюсь, так что двигаемся дальше.

Если внедряете в программу готовый алгоритм (свой или чужой, не суть), очень важно сначала выяснить, можем ли мы вообще его себе позволить (память) и нет ли альтернатив пошустрее (время).

Давайте разберем, что значит голая запись O(n), в отрыве от времени, памяти и алгоритмов. Да-да, извиняюсь, нам придется немножко взглянуть на математику. Математику класса примерно 8-го, так что без паники.

Big O Notation имеет несколько простых правил.
Воспринимаем это пока что как "игру" с числами и функциями.

Итак, правило номер раз: константы откидываются. Нас интересует только кусок, зависящий от размера входных данных, и всё, что "сильно" на него влияет.

Простыми словами - нас интересует только кусок с n, его степени, логарифмы и факториалы, а также экспоненты, где n находится в степени числа или n.

Вот несколько простых примеров:

Правило номер два: если внутри O есть сумма, то нас интересует только наиболее быстро растущий кусок это суммы. Это называется "Асимптотическая оценка функции сложности".

Хорошая новость: правил было всего два, и мы с ними уже разобрались.

Плохая новость: все ещё не видно ни одного алгоритма. Осталось совсем немножко!

Поговорим про сценарии.

У каждого алгоритма часто рассматривают три "варианта" или "сценария" его работы, в зависимости от "удачности" вводных данных: наихудший, средний и наилучший.

Их ещё часто называют случаями.

Наихудший случай, он же Worst Case - вариант работы алгоритма на наименее выгодных вводных данных, требующий максимальный затрат времени и памяти.

Например, если мы хотим отсортировать массив по возрастанию (Ascending Order, коротко ASC), то для многих простых алгоритмов сортировки наихудшим случаем будет вводный массив, отсортированный по убыванию (Descending Order, коротко DESC).

Для алгоритма поиска элемента в неотсортированном массиве (до такого алгоритма мы доберемся с минуты на минуту) наименее выгодный случай имеет место, если искомый элемент находится в самом конце массива, или если элемента там вообще нет.

Наилучший случай, он же Best Case - полная противоположность Worst Case. Самые удачные вводные данные. Правильно отсортированный массив, с которым алгоритму сортировки вообще ничего делать не нужно.

В случае поиска - попадание в нужный элемент с первого раза. Надеюсь, идея ясна.

Средний случай, Average Case - самый хитрый из троицы. Интуитивно ясно, что он всегда сидит между Best Case и Worst Case. Далеко не всегда ясно, где именно.

Очень часто он совпадает с Worst Case, всегда (за категоричность базара не отвечаю) хуже Best Case, если Best Case не совпадает с Worst Case (и такое бывает).

Средний он в плане статистической усредненности.

Берём алгоритм, гоняем его с разными данными много-много раз, по результатам составляем сводку, смотрим, вокруг какой функции распределились результаты.

Расчет Average Case - штука большая и часто сложная, поэтому перечитываем предыдущее предложение (для начала этой информации с головой) и двигаемся дальше!

Настало время алгоритмов. Поговорим про самый-самый простой алгоритм. Мне буквально не приходит в голову осмысленный алгоритм, который был бы проще следующего товарища.

Речь пойдет про линейный поиск, он же Linear Search.

Я предположу, чтоб не раздувать лишний раз и так безбожно раздутый хронометраж, что вы знаете, что такое числа (во валит гад), и знаете, как устроены массивы (набор ячеек для элементов с приколоченными к каждой ячейке числами-индексами).

Дано: массив целых чисел по имени arr, содержащий некоторое количеством элементов. Скажем для формальности, что в нём n элементов (количество элементов, размер строк, а так же размер массивов, списков и графов и в алгоритмах вообще постоянно обозначают как n или N).

Также дано некоторое целое число, обозначим его как x. Для простоты пока что скажем, что x гарантированно содержится в arr.

Задача алгоритма: найти, на каком месте в массиве arr находится число x, и вернуть (тобишь выдать по завершению работы алгоритма в качестве результата) индекс этого элемента.

Возьмём простой пример для arr. Будем искать номер ячейки, содержащую цифру 3.

Как меткий человеческий глаз может увидеть, искомый элемент содержится в ячейке с индексом два, то есть в arr[2].

Менее зоркий компьютер будет вынужден перебирать ячейки друг за другом, arr[0], arr[1]... и так далее, пока не будет найдена тройка либо встречен конец массива, если тройки в нём нет.

Какой тут Worst Case? Больше всего шагов потребовалось бы, если бы искомое число стояло в самом правом конце массива. Нам бы потребовалось пройтись через весь массив (n ячеек) и для каждой ячейки прочитать ее содержимое и сравнить его с искомым числом. Выходит Worst Case: O(n).

В нашем массиве [7,4,3,8,1,2] Worst Case наблюдался бы при x=2.

Что скажете про Best Case? Если бы искомое число стояло бы в самом начале массива, то ответ был бы получен уже на первой ячейке, и дальше никуда ехать не нужно.

Best Case линейного поиска - O(1). Я об этом ранее говорил, но немного вскользь - именно так обозначается константное время в Big O Notation.

В нашем массиве [7,4,3,8,1,2] Best Case наблюдался бы при x=7.

Последний случай, Average Case, каков он?

Если просто и душно - при такой постановке вопроса результаты будут равномерно распределены по массиву. В случае равномерного распределения центр будет располагаться (сюрприз) в середине массива.

Какое число у нас между 1 и n? Вообще-то (n+1)/2, но мы округлим и скажем n/2. Что мы делаем с константами? Правильно, отбрасываем. Получаем Average Case равным O(n).

Хотя в случае Average Case константы иногда оставляют стоять, и запись O(n/2) даст чуть больше интересующей информации. Особого соглашения в науке по этому поводу нет, поэтому делаем выводы и учимся тому, что O(n) для O(n) рознь.

Хорошо, мы уже минуты три говорим про Linear Search, но все ещё не увидели его в виде кода! Ты издеваешься?!

Секунду терпения, я не просто так задержал этот момент. И даже не из вредности!
Перед тем, как показывать код, мы должны обсудить одну очень интимную тему. Называется она - "псевдокод".

Дед, ты о чём вообще? У нас есть код, джава, плюсы, питон на худой конец, зачем нам какой-то "псевдо"-код? Таблетки пей!

Штука, на самом деле, крайне полезная. Сейчас постараюсь в трёх словах рассказать, почему.

Мы все пишем на разных языках. Некоторые похожи, некоторые сильно различаются между собой.

Очень часто мы точно знаем, какую операцию имеем в виду, но не уверены, как именно она выглядит в конкретном языке. За примерами далеко ходить не надо: получение длины массива.

По эволюционно-историческим причинам практически во всех языках используется разная формулировка этого нехитрого действия. .length, length(), len(), size(), .size - попробуй угадай! Фигурные скобочки или отступы? Круглые скобочки в условиях или обойдемся без них?

- Как вообще объяснить свой код коллегам, которые пишут на другом языке?!

Задача псевдокода - вручить нам инструмент достаточно формального, но не слишком требовательного к мелочам, инструмента для изложения мыслей, оторванного от конкретных языков программирования.

Как выглядит этот самый псевдокод? Что ж, it depends, так сказать. В том-то и прелесть, что конкретных правил написания псевдокода нет.

Лично я предпочитаю использовать определенную смесь синтаксиса питона и C, используя отступы для обозначения вложенности, а так же питоновский стиль именования методов.

Вот пример вышеупомянутого псевдокода для нашей маленькой задачи, со всеми допущениями и упрощениями.

Давайте для полноты картины дополним псевдокод двумя случаями и маленьким комментарием - метод должен возвращать число -1, если массив пуст или если x вообще не был найден в arr. Иначе как-то странно и неполноценно выйдет...

На заметку: -1 часто используется в псевдокоде, как invalid index, а если алгоритм возвращает объекты, то часто используют null, nil (то же самое, что и null), а так же специальный символ "ничего", выглядящий как перевёрнутая на 180 градусов буква т.

Также в псевдокоде встречаются конструкции для исключений, вроде throw error("Very Bad").

Кстати, для создания картинок с кодом я использую carbon.now.sh с темой One Dark. Очень удобно!

Написание псевдокода на бумаге или на доске может очень пригодиться в жизни. Первое пришедшее в голову применение - решение задач на белой доске на технических собеседованиях.

Моё написание кода на бумаге и на досках похоже на написанный сверху псевдокод, но с одним маленьким отличием: я люблю явно рисовать все отступы, иначе строчки кода едут, куда глаза глядят.

Вот так моими корявеньким почерком выглядел бы последний пример псевдокода на бумаге:

Первый алгоритм разобран, поздравляю!

Двигаемся к следующей остановке. Остановка называется Binary Search, она же бинарный поиск, она же двоичный поиск. Я предпочитаю называть его бинарным, но это дело вкуса.

В чём его суть и отличие от уже знакомого и любимого линейного поиска?

Во-первых, он предъявляет требования к массиву arr. Массив должен быть отсортирован, в нашем случае - по возрастанию. Надеюсь, с отсортированным массивом чисел проблем не возникнет. Правда же? Числа маленькие в начале, числа большие в конце. Математика четвертый класс.

Для наглядного объяснения Binary Search часто используют пример с телефонным справочником (привет @cs50). Может быть, многие из вас никогда и не видели такую приблуду - это большая книга со списками телефонных номеров людей, отсортированная по фамилиям и именам жителей.

Давайте для простоты забудем про имена, ладно?

Итак, у нас есть огромный, огромный справочник на тысячу страниц, в котором десятки тысяч пар (Фамилия:Номер), отсортированный по фамилиям.

Мы знаем фамилию человека, пусть она будет Жила, и очень-очень хотим найти его номер. Странная фамилия, кто вообще так человека бы назвал, ну да ладно.

Как бы действовал наш предыдущий гость, линейный поиск? Он бы открыл книгу и начал бы её перебирать, строчка за строчкой, страница за страницей: Астафьев...Безье...Варнава...Ги...

До товарища Жилы он бы дошел за пару часов, а вот господин Янтарный заставил бы алгоритм потеть ещё дольше.

Бинарный поиск мудрее и хитрее. Он открывает книгу ровно посередине. Открывает и видит, например, фамилию Мельник. Буква "М" на барабане.

Помним, что книга отсортирована по фамилиям, и алгоритм знает, что буква "Ж" идёт раньше буквы "М".

Следующим делом он берёт, и разрывает открытую на фамилии Мельник книгу пополам (расточительно, но не суть), и выкидывает часть с буквами "Н", "О", "П" ... "Я".

Дальше он берет и снова открывает оставшуюся половинку книги посередине. На этот раз на фамилии Ежов. Близко, но Ежов не Жила, а ещё буква "Ж" идет после буквы "Е". Книга разрывается пополам, левая половинка с буквами от "А" до "Е" выбрасывается.

И так наш алгоритм делает до тех пор, пока у него в руке не останется одна-единственная измятая страничка, на которой рядышком с заветной фамилией находится нужный номер. Занавес. Слёзы счастья...

Давайте теперь перенесем тот же принцип на массивы!

Итак, отсортированный массив arr и число x, которое нужно найти в массиве. Почему поиск называется бинарным?

Дело в том, что алгоритм на каждом шаге уменьшает проблему в два раза. Как? Буквально отрезая на каждом шаге половину массива, в котором гарантированно не содержится наш x.

Алгоритм как бы принимает двоичные решения, разделяя массив на левую и правую половину.

Возьмём, например, такой массив arr, и будем искать в нём число 7.

Всё работает так же, как в примере с телефонной книгой. Мы проверяем только серединку, и если в ней стоит семерка- проблема решена, если меньше семерки- отрезаем левую половину и ищем дальше в правой половине, а если больше семерки- отрезаем правую половину и ищем в левой.

Почему это работает? Вспомните про требование к отсортированности массива, и всё встанет на свои места!

Итак, смотрим в серединку. Милый карандашик будет служить нам "указателем".

В серединке число 5, 5 меньше 7, отрезаем левую половину и проверенное число. В помойку! Смотрим в серединку оставшегося массива:

В серединке число 8, 8 больше 7, отрезаем правую половинку и проверенное число. Смотрим в серединку (хоть там и всего один элемент). Поздравляю, мы нашли искомое число!

Теперь давайте посмотрим на ровно то же самое, только в виде красивого псевдокода. Серединку мы по классике назовём mid, а вместо вычёркивания будем перемещать "окно наблюдения", организованное двумя индексами - low (левая граница) и high (правая граница).

Алгоритм организован рекурсивно (вызывает сам себя на строчке 7 и 9). Итеративный (с циклом, без рекурсии) вариант существует, но кажется мне несколько уродливее. Если ничего не нашли, возвращаем -1 в качестве invalid index.

В начале работы значение low совпадает с началом массива, а high - с его концом. И они бегут на встречу друг другу...

Для того, что мочь удобно запустить бинарный поиск, не задумываясь лишний раз про начальные значения индексов low и high, можно написать такую функцию-обёртку:

Какая будет сложность у бинарного поиска? Best Case, как и у линейного поиска, прост - O(1), ведь искомый x может находиться в серединке массива и быть обнаружен с первой попытки.

Worst Case чуть-чуть больше "на подумать". Каждый шаг рекурсии уменьшает проблему вдвое. Worst Case сводится к вопросу "Сколько раз нам нужно поделить массив на два, чтоб в нём остался один элемент?". Или наоборот нужно найти такое минимальное число k, которое выполняет 2^k ≥ n.

Логарифмы проходят классе в десятом, и я надеюсь, что k найти задача для многих посильная. Если что, задача будет решена для k = log n (по основанию 2, в алгоритмах практически все логарифмы двоичные)

Поэтому Worst Case бинарного поиска будет O(logn).

Что с Average Case? Не буду углубляться, только скажу, что для бинарного поиска Average Case тоже O(logn), и если для линейного поиска Average Case в два раза лучше Worst Case, то тут они обычно отличаются на несколько пунктов, а не в два раза.

Часто студентам (и мне в том числе) приходит в голову вопрос:
-"Зачем нам вообще нужен тогда нужен линейный поиск, если бинарный его бьет по всем позициям?".

Хочу сконцентрировать внимание на этом моменте! Линейный поиск работает на любом массиве, бинарный требует отсортированного массива на входе.

Это отличный пример того, как ускорение достигается за счёт применения более сложной структуры данных (обычный массив vs отсортированный).

Сортировка, в свою очередь, более сложная и дорогая операция. Забегу наперёд и скажу, что сортировка в общем случае требует от O(n*log(n)) до O(n^2) времени.

Повторим для закрепления: Более сложная структура данных -> возможность использовать более быстрые алгоритмы.

Создать дополнительные структуры данных несложно, вот только они не бесплатны. Они жрут память. Много памяти. В основном, речь идёт об O(n) для памяти.

Из этого факта вытекает довольно логичная, но обидная мысль: Время и Память являются до некоторой степени "обмениваемыми" ресурсами. Если коротко и не по-русски, то это трейдофф.

Можно ускорить алгоритм, пожертвовав потреблением памяти, или решать проблему медленно, зато in-place. Практически всегда существует ещё и компромиссный вариант.

Для решения одной и той же проблемы зачастую есть алгоритмы всех трёх видов. Задача разработчика - понять предметную область и спецификации, и выбрать более подходящий для конкретного случая алгоритм!

Уф, почти высокая философия. С такими речами точно можно книгу издавать, а лучше сразу свои инстаграм-курсы. Двигаемся дальше!

Уф, почти высокая философия. С такими речами точно можно книгу издавать, а лучше сразу свои инстаграм-курсы. Двигаемся дальше!

Первый, и наиболее часто используемый способ - "на глаз прикинуть". Что это значит? Именно этим мы занимались в примерах с Linear Sort и Binary Sort. Как генерализировать эти примеры?

Представлю два самых простых случая.

Случай номер раз: у нас есть алгоритм (some_function), который выполняет некоторое действие А, а после него действие В. На А и В нужно K и J операций, соответственно.

В случае такого "последовательного" выполнения очень просто увидеть сложность алгоритма - это O(K + J), а значит O(max(K, J)).

Например, если А квадратичный (n^2), а В линейный (n), то сложность будет O(n^2 + n), а мы уже выяснили, что нас интересует только самый быстрорастущий кусок - тобишь O(n^2)

Случай номер два: действия или вызовы методов в циклах.

Размер массива это n, без ограничений по размеру. Для каждого элемента массива будет выполнено некое действие А. То есть n раз. Дальнейшее развитие событий зависит от сложности действия А.

Если мы знаем, что в нем содержится, например, гарантированно 5 операций, то всё просто: O(n * 5) = O(n).

А если в А, например, используется массив arr целиком, и совершается n операций? Тогда в алгоритме n раз будет совершено n операций, получаем O(n * n) = O(n^2). По такой же логике можно получить O(nlogn), O(n^3) и далее по списку.

Давайте для закрепления посмотрим на пример, в котором собраны оба случая воедино. Допустим, что действие А требует log(n) операций, а действие В требует n операций. На всякий случай напомню, меня самого это поначалу вечно путало: в алгоритмах всегда имеется в виду log2.

Накинем ещё действие С с пятью операциями. Что мы получаем в итоге?

O(n * (n * log(n) + n) + 5) =

O(n^2 * log(n) + n^2 + 5) =

O(n^2 * log(n))

Мы видим, что самым дорогим куском алгоритма является действие А, которое выполняется в цикле, который выполняется в цикле, и именно он "доминирует" во всей функции.

Относительно редким, но достойным упоминания гостем является так называемый "Амортизационный анализ".

Если в двух словах, и не писать отдельный тред на его тему: если на X "дешёвых" операций (например, с O(1)) у нас есть одна "дорогая" операция (например, с O(n)), то на большом количестве операций (большое значение X) температура по больнице выйдет практически неотличимой от O(1)

Не Sort, а Search, конечно же

Практически каноничным пациентом для амортизационного анализа являются динамические массивы. Это такие массивы, которые при переполнении создают новый массив, больше оригинала в 2 раза, копируют свои элементы в него, а потом подменяют ссылку на новый.

Замена ведра на ведро побольше с сопутствующим переливанием содержимого, если угодна аналогия. Так вот: практически всегда добавление элементов в такой массив "дешево" - требуется лишь 1 операция.

Когда он заполняется, требуются усилия на создание нового массива и копирования старых N элементов в новый.

Так как массив каждый раз увеличивается в два раза, ситуации переполнения становятся все реже и реже, и Average Case добавления элемента в такой массив остается в рамках O(1).

Я думаю, для наглядного примера метода "на глаз прикинуть" - с головой. Какие ещё есть способы?

Слабое место прикидывания на глаз - рекурсия. С ней правда сложновато. Так вот, для оценки сложности рекурсивных алгоритмов широко используется Мастер Теорема.

По сути, это набор правил по оценке сложности, основывающийся на том, сколько новых ветвей рекурсии создается на каждом шаге, и на сколько кусков дробятся данные в каждом шаге рекурсии. Это если вкратце, а более детально о Мастер Теореме я бы поговорил в отдельном треде.

Повторюсь, для закрепления, если рекурсия с приколами - оцениваем правилами из Мастер Теоремы.

Последний способ оценки ближе к Data Science и нумерике. Мы берем алгоритм, и гоняем его на рандомных данных разного размера, и производим замеры времени и памяти.

Эти замеры приземляются на графиках (отдельный для памяти и отдельный для времени) и потом автоматически ищется функция, которая лучше всего описывает это "облако точек".

Возможно, это справедливо назвать методом Монте-Карло для оценки алгоритмов. В названии я не уверен, но в чем вообще можно быть уверенным?

Этот способ применяется только если первые два применить не является возможным. Особенно его любят, если нужно описать сложность не одного алгоритма, а производительность целой системы, состоящей из множества алгоритмов.

Первых двух нам хватит с головой на всю серию тредов про алгоритмы. Третий - довольно редкая штука.

Добавим этой истории немножко научности. Инструмент, который мы использовали на протяжении всего треда - Big O Notation - это только одна из пяти встречающихся нотаций. Вот они слева направо: Намджун, Чонгук, Чингачгук...простите, не удержался.

Сверху вниз: Small o, Big O, Big Theta, Big Omega, Small omega. f это "реальная" функция сложности нашего алгоритма, а g - его "асимптотическая" функция сложности.

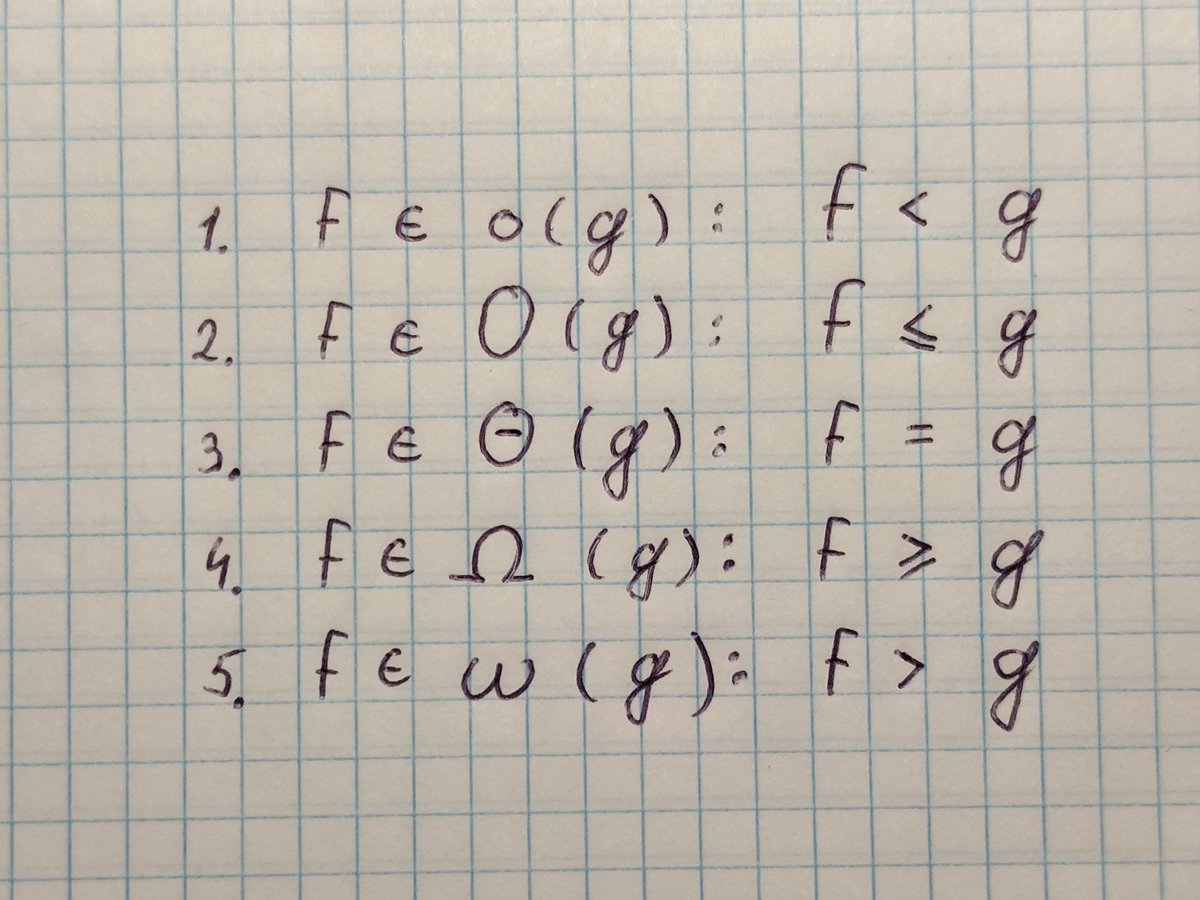
Оброню несколько слов об этой весёлой компании. Наше знакомое Big O обозначает верхнюю границу сложности алгоритма, и является идеальным инструментом для Worst Case.

В свою очередь, Big Omega (которая пишется как подкова) обозначает нижнюю границу сложности алгоритма, и её правильнее использовать для Best Case.

А Big Theta (пишется как О с чёрточкой) располагается между О и Омегой, и показывает "точную" функцию сложности алгоритма. Для Average Case правильнее использовать её.

"Правильнее", в контексте пейперов по алгоритмам с кучей математики, а в статьях в интернете и в рабочей документации в подавляющем большинстве случаев используется Большое О для всех трёх случаев.

Последние два варианта (Small o и Small omega) находятся по краям этой иерархии и используются в основном для сравнения разных алгоритмов между собой.

Тема немножко специфическая, я думаю, что в рамках основ такого обзора - с головой. Вот хороший видос на эту тему, если кому интересно узнать об остальных нотациях побольше:

Думаю, что будет очень полезным показать наглядно, насколько сильно отличаются скорости возрастания различных функций.

Вот хороший cheat sheet по сложности алгоритмов: bigocheatsheet.com

...и очень наглядная картинка с графиками функций, украденная прямиком оттуда!

Правда, хоть картинка и наглядная, я не уверен, что она хорошо передает всю бездну, лежащую между этими функциями.

По этой причине я склепал таблицу, где для разных функций представлены значения времени для разных N. За время одной операции возьму 1 наносекунду (10^-9 секунду). Это, в целом, очень реалистичное значение.

Последняя мысль будет про константы. А именно скрытые константы, они же Hidden Constants. Это штука хитрая, там собака зарыта.

Возьмём простую штуку, умножение матриц. При размерности матриц n x n, "наивный" (так называют алгоритмы, решающие проблему в лоб, brute force, так сказать) алгоритм, который многие знают с начальных курсов универа - строчка на столбик - имеет кубическую сложность, O(n^3).

Кстати об умножении матриц - про него у меня был отдельный тред:

https://twitter.com/ValeriiZhyla/status/1447493685323739136

Кубическая, зато честная, без констант, никаких O(10000 * n^3) под капотом. И памяти не ест, только время.

Существуют алгоритмы умножения матриц, в которых степень n сильно порезана. Самые "быстрые" алгоритмы пляшут около O(n^2.37). Какой персик, правда? Почему бы нам не забыть про "наивный" алгоритм?

Проблема в том, что эти "быстрые" алгоритмы имеют огромные константы. В пейперах гонятся за более компактной экспонентой, а степени отбрасываются. Я честно искал, но не нашел внятных цифр констант, даже авторы оригинальных пейперов называют их просто "очень большими".

Давайте с балды возьмём "не очень большую константу", 100. И сравним n^3 c 100 * n^2.37.

Я посчитал за вас, но можете конечно меня перепроверить, что правая функция дает выигрыш по сравнению с левой для n, начинающихся с 1495. А это мы взяли довольно скромную константу, я подозреваю, что в реальности они не в пример больше...

В свою очередь, умножение матриц 1495х1495 - очень-очень специфическая вещь. Матрицы миллиард на миллиард точно нигде не встретишь (давай, Император Душнил с хабра, приди и поправь моё вольное допущение).

Такие алгоритмы называются "галактическими" - потому что они дают выигрыш только на масштабах, практически нерелевантных для нас. Вот вам и скрытые константы.

А в программном умножении матриц, если я правильно помню курс алгоритмов и умею читать википедию, очень любят алгоритм Штрассена с его O(2.807) и маленькими константами (но жрущим память аки чорт, так что не панацея).

Вот, собственно, и всё, что я хотел сказать про Big O Notation. В следующем треде (который, кстати, уже в работе) я расскажу о трёх самый простых алгоритмах сортировки, об их проблемах, прелестях и возможностях ускорения.

Эту троицу зовут BubbleSort, SelectionSort и InsertionSort. По причинам объема (и моей лени) они не попали в этот тред. А дальше нас ждут треды по MergeSort и QuickSort!

Надеюсь, что вышло разложить всё по полочкам!

Как всегда, постараюсь ответить на все возникшие вопросы, и среагировать, если я где-то напорол.

@threadreaderapp unroll

Кстати, все мои треды теперь можно прочитать в форме pdf документа на гитхабе!
github.com/OratorX/twitte…