Thread by @mattecapu

Today Dylan Braithwaite, @bgavran3, @_julesh_, @AyeGill and myself published the extended abstract of a work that has been cooking for quite a bit (at least a year!)

arxiv.org/abs/2112.11145

What's in there? 1/n

The problem we're trying to solve is to 'complete this square'. Lenses are modular data accessors for records (i.e. pairs), dep. lenses are modula data accessors for records *with dependency* (i.e. dependent pairs), whereas optics extend lenses to obscene levels of generality 2/n

In particular, optics provide an abstract framework for defining 'lens-like' accessors for structures with much more complexity than records (e.g. trees) and for more exotic accessing patterns (e.g. with monadic effects)
See arxiv.org/abs/1703.10857 and arxiv.org/abs/2001.07488 3/n

For us cybercats people, optics have a different meaning: they abstract bidirectional information flow, thus modelling feedback systems (e.g. games arxiv.org/abs/1910.03656, AI arxiv.org/abs/2103.01931, cybernetic systems matteocapucci.wordpress.com/2021/05/26/ope…) 4/n

OTOH, dependent lenses (under the guise of 'Poly') are also proving useful in modelling (cybernetic) systems, the main reason being they allow dynamics to properly depend on the environment 'input'. In the words of @david_i_spivak, they allow *mode-dependent* dynamics 5/n

Mathematically, this is manifested by the fact the category of dependent lenses has *all* coproducts. This allows to join systems in a composite systems which conditionally runs either of the composee, depending on the choice the environment makes 6/n

This is *very* useful for open games. In our last paper on games, we describe an operator (&) on games which models exactly this external choice. It is crucial to model swiftly even the simplest games arising from their 'extensive form' description 7/n

This is even more useful in 'open servers', a cybercat description of REST APIs I've been working on with @andre_videla (who first realized parametrised lenses are a great abstraction for them) 8/n

So dependent lenses are great, and that's why Poly has been taking off in the last year.
Except... they have the same limitations normal lenses have: they rely crucially on the *cartesian* and *cocartesian* monoidal structures of Set, which are not available for cats like... 9/n

...those of stochastic/non-deterministic maps or even just stateful/effectful maps. E.g., Bayesian open games (arxiv.org/abs/1910.03656) are crucially affected by this lack of cartesianity, and so are servers if one wants to model concurrency fairly well 10/n

(Interlude: cartesianity is famously 'evil' in categorical systems theory because it breaks linearity, i.e. non-cloning of resources. In a cartesian cat, all objects have a diagonal X→X×X which clones stuff, and that's a buzz kill for e.g. concurrency and quantum) 10bis/n

In the non-dependent case, cartesianity is waived and one can use just monoidal products (or even actions of monoidal cats) to define categories of lens-like things using optics.
So a challenge was on: can you define 'dependent optics'? 11/n

This means adding dependent structure in a way which is compatible and orthogonal to the monoidal/actegorical structure.
Various attempts have been tried, and finally we made a dent in the problem this spring when @AyeGill realised a 'minimum viable definition' of... 12/n

...'dependent optics' could be simply 'coproduct completion of optics'.
As every good idea, in its essense it's devilishly simple: you just *add* the coproducts you need and construct a category of 'synthetic bundles', i.e. formal sums of pairs of objects 13/n

We called them 'indexed optics' as they are pretty literally indexed families of optics.
Meanwhile, @BartoszMilewski independently came up with a very similar construction and gave it a brilliant name, ommatidia, after insects composite eyes: 14/n

This definition is related to a generalisation of 'enriched' polynomial functors, and I guess that's why Bartosz started calling them PolyLens 15/n bartoszmilewski.com/2021/12/07/pol…

But we were greedy, and continued wondering: can we do better? After all, the definition of indexed optics is still quite heavy on the assumptions: it relinquishes cartesianity, but asks *a lot* of coproducts in exchange! 16/n

Most importantly, the way it models dependency is laughable: we formally stitch together pairs, and that's satisfactory only when our situation involves 'discrete' types, e.g. sets. What about measure spaces? Manifolds? 17/n

That's where fibrations came in. Concurrently to the indexed optics line of research, me and @bgavran3 have been investigating exotic ways to define optics, especially involving (2-)fibrations and the 2-Grothendieck construction. 18/n

A long time ago we stumbled upon a curious fact: if we let go of the coend in the definition of optics, we can create a bicategory of optics with explicit slidings, and that's apparently fibered over Copara(C) 19/n

(Interlude: Para and Copara are constructions that turn an actegory in a bicategory. They're the categorified versions of the action category construction, and they are central in our approach to categorical cybernetics. See arxiv.org/abs/2105.06332 for a definition) 19bis/n

After a long time sitting on it, we realized the solution of the indexed optics inadequacies could lie in a fibrational approach, whose details Eigil ironed out.
That's fiber optics!
For details on that (it's quite technical), see the paper 20/n

Finally, when we were pondering on the 'true definition' of dependent optics, we stumbled upon another, big idea: optics are 2-fibered over Copara *because they arise as the pullback of Para and Copara over the delooping of the acting category* 21/n

That's fantastic insight. First of all, it finally show how optics are coupled pairs of coparametrised and parametrised morphisms: that's the pullback conditions in action! 22/n

Secondly, it neatly presented the structure of optics 'globally', in a very conceptual way: 23/n

Let me dwell a bit on this point:
1. It gives a recipe for optics: get a bicategory of residuals, get a 2-fibration and a 2-opfibration over it, pullback
2. It exposes hidden structure in optics: there's a 'trivial' object∗in every object, and residuals are morphisms too 24/n

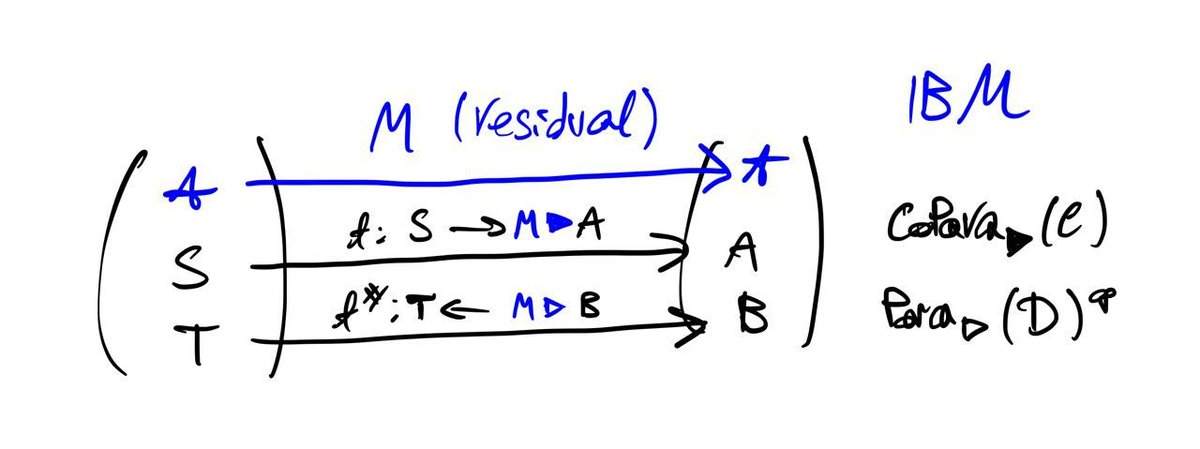
Also, it conceptualizes the fact optics are morphisms of 'generalised bundles', i.e. bundles formalised by a fibration instead of being given by explicit maps in a category (i'm borrowing @myers_jaz terminology here) 25/n

You see how this helps with indexing/dependency: you can now generalize from one-object bicategories of residuals to bona fide bicategories, and the many objects provide a way to encode dependency in the objects. This is what we did 'manually' for fiber optics 26/n

Moreover, profunctor encoding of optics hints to the same story: optics are defined as structure-preserving morphisms of 'virtual bundles', whose structure is only known and specified through the category of profunctors describing their possible sections. 27/n

Instead, here we are explicitly specifying domain and codomain projections for these bundles and defining optics explicitly as morphisms which 'agree' on the exchanged residual 28/n

Exploring how much depth really is in this idea is still work in progress. In particular, we are still pondering which restrictions does it make sense to put on functors projecting residuals out of forwards and backwards parts. Shall they be a 2-fib and a 2-opfib? 29/n

Shall they be given by the generalised version of copara and para for 'actions of bicategories'? But most importantly, are there new examples captured by this definition?
30/n

Regarding the latter, we have some good news. All the known examples of optics and dep. lenses are captured by this 'definition'!
31/n

Indeed, we've got very excited when we realised one could construct lenses in a completely new and conceptual way using this definition.
The cosmic cube was born (green means oplax): 32/n

The cube relates the two constructions of the category of lenses. On the bottom face, we construct it the 'new way', by explicitly specifying forward, backward and residual parts. The crucial definitions are those of the oplax functors 'dom' and 'copy': 33/n

The cosmic cube *does not* commute in bicategories, it only commutes when we 'locally quotient' the bicategories to get back to 1-cats world. The local quotient is given by 'taking connected components'.
34/n

Since two optics (as given by the pullback in the top face) are connected when there's a sliding from the forward to the backward part, you see this recovers the quotient usually expressed through a coend.
In the cosmic cube, green arrows become black, ...
35/n

and bicategories collapse (in particular, Copara(C) becomes C!), until all that remains is a cube commuting by UP of the pullback, with an equivalence of cats linking 'cartesian optics' and 'lenses' 36/n

One can also recover fiber optics as a pullback. In doing so, one realises how they arise as very particular arrangement of residuals in a category of matrices (something we notice before, but not with this clarity).
In the end, all comes down to linear algebra. 37/n=37.

I forgot: F-lenses are a trivial instance of this pullback construction. The identity as the forward part is witnessing the fact F-lenses are a kind of dependent optics in which 'forward part = residual part' 38/37

https://twitter.com/mattecapu/status/1473592884108705792?s=20

In the particular case of dependent lenses, we speculate a more refined (or crazy) description is available, but we still didn't check all the details.
It's similar to the description of lenses in the cosmic cube, and thus we call it the cosmic dependent cube: 39/37

The two cosmic cubes fit together in an even more speculative 'cosmic tesseract', which is cool to say and even cooler to look at: 40/37

(This reminds me to thank @varkora again for the wonderful thing quiver is. For instance, here's the URL for the cosmic tesseract q.uiver.app/?q=WzAsMTYsWzY…)