Thread by @jorgeluisaliaga

CRECIMIENTO EXPONENCIAL - Sale Hilo.
Se suele usar como sinónimo de algo que crece “mucho”.
Pero en realidad es un tipo particular de crecimiento.

Uno puede tener un crecimiento “lineal”.
Se obtiene sumando siempre una misma cantidad.
Supongamos que vamos sumando 1 a cada paso.
Pasaremos de 1 a 1+1=2, luego 1+1+1=3, luego 1+1+1+1=4 y así siguiendo.
Podemos visualizarlo viendo como crece una línea:

Si vemos paso a paso como va creciendo la flecha a medida que aumentan los pasos, el largo de la flecha crece como una recta a medida que aumenta el número de pasos.

La VELOCIDAD es la cantidad de avance por paso.
Con crecimiento lineal la velocidad es CONSTANTE, siempre igual.
Es equivalente a caminar a una velocidad de una cuadra por minuto. Luego de 25 minutos (pasos) recorro 25 cuadras.

La ACELERACIÓN es cuanto cambia la velocidad entre un paso y otro. Con crecimiento lineal la aceleración es cero, voy siempre a la misma velocidad, ni más rápido ni más lento.

Si en lugar de sumar uno a cada paso sumamos DOS, obtenemos 2, 2+2=4, 2+2+2=8, 2+2+2+2=16 y así siguiendo

Si vemos paso a paso como va creciendo la flecha a medida que aumentan los pasos, el largo de la flecha también crece como una recta, pero avanza más rápido.
Sería equivalente a caminar a una velocidad de dos cuadras por minuto. Luego de 25 minutos (pasos) recorro 50 cuadras.

La velocidad es el doble que en el ejemplo anterior, pero la aceleración sigue siendo cero.

Ahora, supongamos que tenemos un crecimiento que NO es lineal. Supongamos que crece como crecen la cantidad de cuadrados que se muestran en estas figuras:

Voy agregando un cuadrado en cada uno de los dos ejes al mismo tiempo, y la cantidad de cuadrados pasa de 1 a 4, luego 9, luego 16, luego 25.

La cantidad de cuadrados se puede calcular multiplicando la cantidad que hay en cada eje: 1*1=1, 2*2=4, 3*3=9, 4*4=16, 5*5=25 Como agrego de a un cuadrado por eje en cada paso obtengo una función “cuadrática”.

Si vemos paso a paso como va creciendo la cantidad de cuadrados, crece como una “parábola”. Crece más rápido que una recta.

Puedo calcular la velocidad viendo cuanto cambia la cantidad acumulada entre cada paso. Si hago esa cuenta veo que la velocidad aumenta linealmente. A medida que recorro pasos voy cada vez más rápido.

Si calculo la aceleración, viendo cuanto cambia la velocidad, resulta que la aceleración es constante. Es decir, la variación de la velocidad entre pasos es siempre la misma.

Ahora, supongamos que vamos agregando CUBOS. Se muestra en estas figuras cómo crece la cantidad de cubos:

Voy agregando un cubo en cada uno de los tres ejes, y la cantidad de cubos pasa de 1 a 8, luego 27, luego 64, luego 125.

La cantidad de cubos se puede calcular multiplicando la cantidad que hay en cada eje: 1*1*1=1, 2*2*2=8, 3*3*3=27, 4*4*4=64, 5*5*5=125. Como agrego de a un cubo por eje obtengo una función “cúbica”.

Si vemos paso a paso como va creciendo la cantidad de cubos, crece como una “cúbica”, más rápido que una recta y que una parábola.

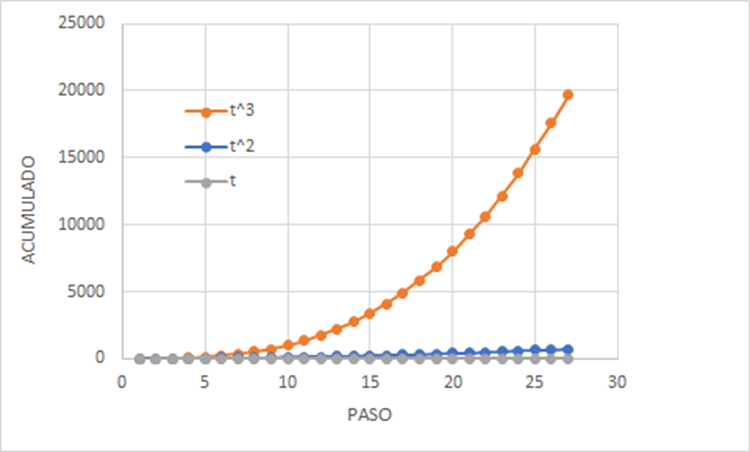
Si calculamos la velocidad, vemos que aumenta como una parábola. Y si calculamos la aceleración vemos que aumenta como una recta. Y si calculáramos la variación de la aceleración entre pasos nos daría una constante.

Todas estas formas de crecimiento se obtienen SUMANDO algo. En el primer caso líneas, en el segundo cuadrados, en el tercero cubos. Todas crecen a distinta velocidad y aceleración, pero todas crecen SUMANDO algo.

Ahora pensemos en una forma distinta de crecer. En lugar de SUMAR algo vamos a MULTIPLICAR por algo.

Empecemos por un ejemplo simple. En cada paso en lugar de sumar 2, multiplico por 2. Si empiezo por 2, en el segundo paso tengo 2*2=4, en el tercero 2*2*2=8, en el cuarto 2*2*2*2=16, en el quinto 2*2*2*2*2=32.

La fórmula de crecimiento en este caso es 2 multiplicado tantas veces como el número de pasos. Eso se resume indicando con un número pequeño y elevado (supraíndice) la cantidad de veces que se multiplica por ese número. Es el EXPONENTE.

Veamos como va creciendo la cantidad acumulada cuando crece de esta forma, exponencial (en cada paso aumenta el exponente):

A lo mejor la forma de la curva no parece muy distinta a las anteriores, pongamos todas en la misma figura:

El crecimiento exponencial es tan grande que el resto de las curvas quedan completamente perdidas. Ampliemos la primera parte para ver el detalle.

Cuando se dan los primeros pasos todas las curvas parecen similares, incluso pareciera que la función exponencial no es la que crece más rápido.

A medida que se van acumulando pasos las distintas formas de crecer se van separando.

Pero cuando los pasos se siguen acumulando la exponencial pasa al resto.

Y el crecimiento exponencial termina siendo superior a todo otro tipo de crecimiento que suma algo en lugar de multiplicarlo.

Una característica del crecimiento exponencial es que si calculo la velocidad, también tiene un crecimiento exponencial. Y si calculo la aceleración, también tiene un crecimiento exponencial.

¿Es posible reconocer en un gráfico cuándo una curva crece sumando y cuando crece multiplicando (crecimiento geométrico o exponencial)? La respuesta es SI.

Los gráficos que usamos hasta ahora usan escalas que son “lineales”. Si uno se fija como cambian tanto los ejes verticales como horizontales siempre se le suma algo.

Por ejemplo en esta figura, en la escala horizontal entre cada división se le suman 5 pasos y en la escala vertical a la cantidad acumulada se le van sumando 20.

Construyamos escalas que, en lugar de sumar una cantidad entre divisiones se multiplique por una cantidad entre divisiones. Es decir, en lugar de 10, 20, 30, … que sea 10, 100, 1000, …
Esas escalas se llaman logarítmicas.

Las mismas curvas anteriores en escalas logarítmicas se ven así.

Las curvas que crecen SUMANDO se ven como RECTAS si ambas escalas son “logarítmicas”. Y la curva que crece MULTIPLICANDO (crecimiento exponencial) NO se ve como una recta (la curva ROJA).

En cambio si dejo la escala vertical logarítmica y la horizontal lineal (escala semi-logarítmica) el crecimiento exponencial se ve como una recta y las que crecen SUMANDO se ven curvas.

Las escalas logarítmicas (o semilogarítmicas) nos permiten ver series de valores que crecen o decrecen mucho, y que si se usan escalas lineales no se aprecian las variaciones:

Un par de puntos más, que son importantes. Si tengo crecimientos que se SUMAN, y en escalas logarítmicas se ven como “rectas”, las pendientes de las rectas nos indican qué tipo de crecimiento es: lineal, cuadrático, cúbico

La recta azul (cuadrática) tiene una pendiente que es el doble de la gris (lineal) y la naranja (cúbica) el triple de la lineal. En un “paso” de la escala horizontal la gris crece una división (10), la azul crece en 2 divisiones (100) y la naranja crece en 3 divisiones (1000).

Si tengo crecimiento que se MULTIPLICA (exponencial), y uso escala semilogarítmica, la pendiente de las rectas me permiten identificar cuál es el factor por el que se multiplica en cada paso.

Pasemos ahora a un ejemplo biológico. Supongamos que tenemos una pareja de conejos. Y que la pareja tiene una pareja de conejos cada mes. La cantidad de crías de esa pareja de conejos va a crecer como muestra esta figura:

Esto es así porque cada mes se SUMAN 2 crías adicionales a las anteriores.

Ahora supongamos que cada pareja que nace, al mes siguiente tiene una pareja de conejos. Empezando en el primer mes la pareja tiene una nueva pareja. Esas dos parejas tienen una nueva pareja cada una. Al mes siguiente esas 4 parejas tienen cuatro parejas nuevas, una cada una.

En este ejemplo la cantidad de conejos se MULTIPLICA.

O, lo mismo visto en escala semilogarítmica (ver que en la escala vertical cada división es 10 veces mayor que la anterior).

Resumiendo, hay muchas formas de crecer “rápido”. Pero crecimiento exponencial es un crecimiento rápido particular, en el que en cada paso el resultado del paso anterior se MULTIPLICA por un número.

Puede sonar raro, pero estamos muy acostumbrados a esto en la vida diaria. Cuando el INDEC anuncia que los precios subieron un 3% en un mes en relación con el mes anterior, eso quiere decir que, en promedio, si las cosas costaban $100 ahora cuestan $103 = 100 + 100 * 3 / 100.

Si al mes siguiente hay nuevamente 3% de inflación, las cosas costarán $103 + $103 * 3/100 = $106,09, NO $106.
Y al mes siguiente, si nuevamente el INDEC anuncia 3% será $106,09 + 106,09 * 3/100 = $109,27.

La inflación anual es el producto de la inflación de cada mes, y no la suma de la inflación de cada mes. La inflación es un típico ejemplo de crecimiento exponencial. Y no depende de si la inflación es 1% o 10% mensual, sino de la forma de crecimiento.

Bueno, pero siempre es mejor que te lo explique Adrián Paenza en Alterados x Pi

(FIN)