La "ℂOMPLEJIDAD" de la EPICICLOIDE ⭕️
¡Dentro hilo! 👇🧵
¡Dentro hilo! 👇🧵
Veamos... ¿qué es una epicicloide? 🤔
Considera una circunferencia que sea tangente exterior a otra y hazla rodar sin deslizarse. Fíjate en uno de sus puntos y traza su trayectoria. A ese trazo lo llamamos EPICICLOIDE.
epi-: encima/sobre...makes sense 😬
Considera una circunferencia que sea tangente exterior a otra y hazla rodar sin deslizarse. Fíjate en uno de sus puntos y traza su trayectoria. A ese trazo lo llamamos EPICICLOIDE.
epi-: encima/sobre...makes sense 😬
¿Adivinas cómo se llama la circunferencia pequeña que GENERA la trayectoria? GENERATRIZ 🖌️
¿Y la grande que DIRIGE a la pequeña? DIRECTRIZ 🔄
Esta nomenclatura no es exclusiva para este tipo de curvas... ¿Quién es quién? 🐶🐢 jeje
¿Y la grande que DIRIGE a la pequeña? DIRECTRIZ 🔄
Esta nomenclatura no es exclusiva para este tipo de curvas... ¿Quién es quién? 🐶🐢 jeje
Miremos más allá...🧐
¿Cómo cambiará la epicicloide si variamos los radios de las circunferencias? ¿Cambiará su forma?
Imagina que multiplicamos el radio de la grande por 2, es decir, R→2R.
Y hacemos lo mismo con el radio de la pequeña: r→2r.
¿Cómo cambiará la epicicloide si variamos los radios de las circunferencias? ¿Cambiará su forma?
Imagina que multiplicamos el radio de la grande por 2, es decir, R→2R.
Y hacemos lo mismo con el radio de la pequeña: r→2r.
Si te fijas, lo único que hemos hecho es cambiar el radio de la directriz y la generatriz, pero como lo hemos hecho con la misma proporción... cambiará el tamaño, pero no la forma. 😳💭
Por lo tanto, la forma de la epicicloide estará vinculada al cociente que relaciona los dos radios: k=R/r.
¿Y si miramos distintos valores de k? En otras palabras, ¿y si variamos R y r con proporciones distintas? Veamos algunos casos.
k=1 (cardioide)
¿Y si miramos distintos valores de k? En otras palabras, ¿y si variamos R y r con proporciones distintas? Veamos algunos casos.
k=1 (cardioide)
k=2 (nefroide)
k=3 (trifolio)
k=4 (cuadrifolio)
¿Ves algún patrón entre cada representación y el valor de k correspondiente?
En efecto, k es el número de cúspides, es decir, de singularidades de la curva (los picos de toda la vida).
Hasta aquí todo bonito porque hemos cogido valores enteros. 🥱 ¿Y si k no fuese entero? 🤭
En efecto, k es el número de cúspides, es decir, de singularidades de la curva (los picos de toda la vida).
Hasta aquí todo bonito porque hemos cogido valores enteros. 🥱 ¿Y si k no fuese entero? 🤭
Veamos qué pinta tiene esta curva y hagámoslo con su expresión ℂompleja.
Como era de esperar, el parámetro de la curva es un ángulo y lo llamaremos θ. Es el ángulo que recorre el CENTRO de la circunferencia peque y mide el número de vueltas que da el CENTRO fuera de la grande.
Como era de esperar, el parámetro de la curva es un ángulo y lo llamaremos θ. Es el ángulo que recorre el CENTRO de la circunferencia peque y mide el número de vueltas que da el CENTRO fuera de la grande.
El primer sumando representa el vector que va desde el origen al centro de la circunferencia peque:
Y el segundo sumando representa el vector que va desde el centro de la circunferencia peque al punto que hemos elegido para pintar la epicicloide:
Por lo tanto, tiene sentido que la suma nos dé las coordenadas del punto elegido.
Como ya hemos visto, las cúspides son los picos de la epicicloide. Estos se hallan en la circunferencia grande y se obtienen cuando los dos vectores tienen orientaciones (argumentos) opuestas.
Como ya hemos visto, las cúspides son los picos de la epicicloide. Estos se hallan en la circunferencia grande y se obtienen cuando los dos vectores tienen orientaciones (argumentos) opuestas.
¿Cuándo los dos argumentos son opuestos?
En otras palabras, ¿en qué ángulos θ están las cúspides?
¡BINGO! Las cúspides se trazan cuando la pequeña ha dado n/k vueltas a la grande, donde n es un número entero. Cada rotación que dé la pequeña sobre ella misma dibujará una cúspide.
En otras palabras, ¿en qué ángulos θ están las cúspides?
¡BINGO! Las cúspides se trazan cuando la pequeña ha dado n/k vueltas a la grande, donde n es un número entero. Cada rotación que dé la pequeña sobre ella misma dibujará una cúspide.
Piensa en los casos anteriores. Por ejemplo, k=3.
Las cúspides se hallaban cuando habíamos dado 0 vueltas, 1/3 de vuelta y 2/3 de vuelta.
Y volvíamos a repetir este mismo ciclo cuando acumulábamos 1 vuelta, 4/3 de vuelta, 5/3 de vuelta...
Las cúspides se hallaban cuando habíamos dado 0 vueltas, 1/3 de vuelta y 2/3 de vuelta.
Y volvíamos a repetir este mismo ciclo cuando acumulábamos 1 vuelta, 4/3 de vuelta, 5/3 de vuelta...
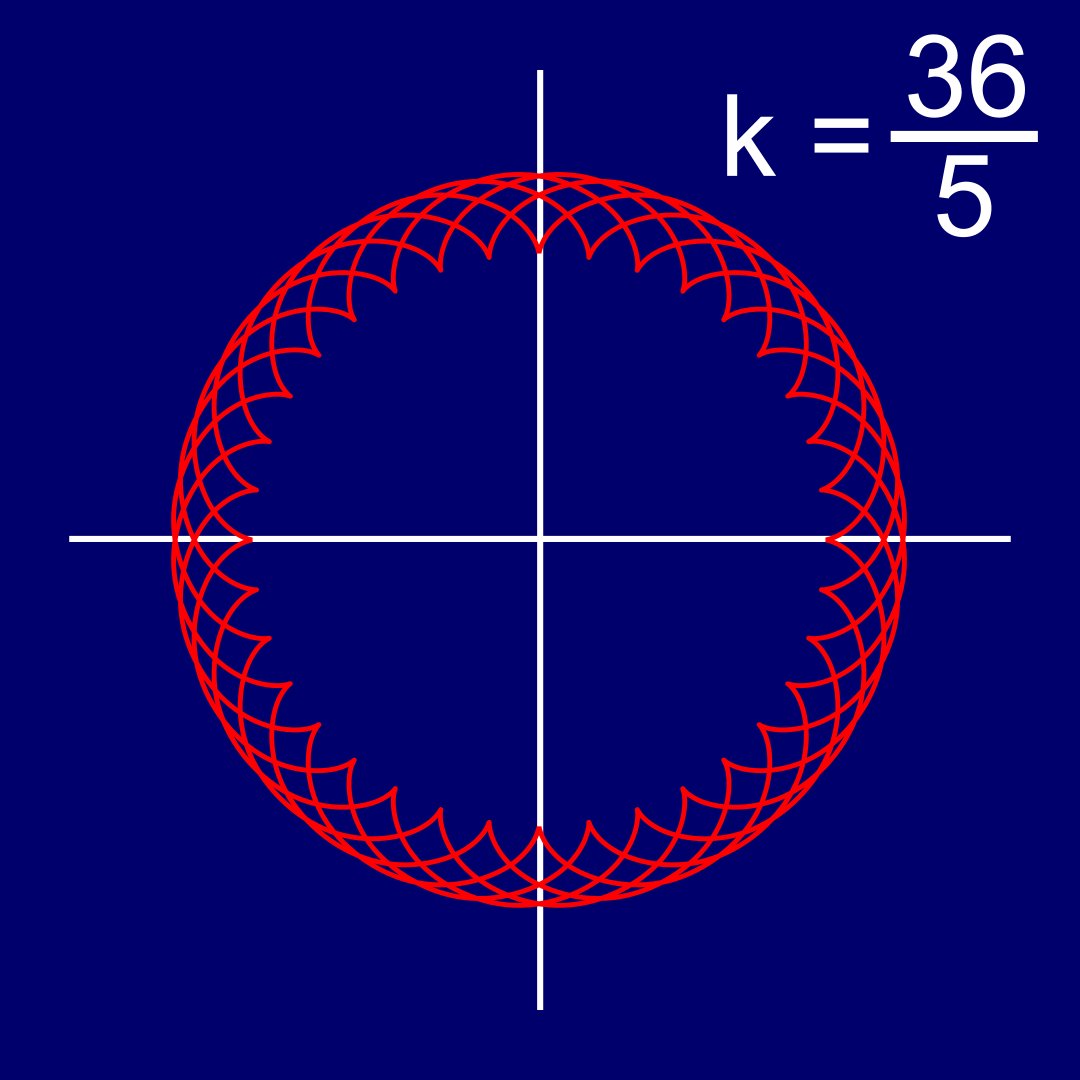
¿Y si k es racional?
Si k∈ℚ, escribimos k=a/b de forma simplificada, donde a,b∈ℤ no tienen divisores en común salvo el 1.
En este caso, las cúspides se encuentra cuando hemos dado n·b/a vueltas.
a: número de cúspides
b: vueltas de la peque a la grande hasta volver al inicio
Si k∈ℚ, escribimos k=a/b de forma simplificada, donde a,b∈ℤ no tienen divisores en común salvo el 1.
En este caso, las cúspides se encuentra cuando hemos dado n·b/a vueltas.
a: número de cúspides
b: vueltas de la peque a la grande hasta volver al inicio
Así lo ilustran los ejemplos:
k=11/2 → 11 cúspides
k=11/2 → 11 cúspides
k=19/5 → 19 cúspides
k=21/10 → 21 cúspides
k=36/5 → 36 cúspides
Por último, podemos pensar qué sucede si k es irracional, es decir, si k no se puede escribir como cociente de dos enteros.
Como las cúspides se dibujan cada n/k vueltas, nunca podremos cerrar el ciclo porque n/k solo podrá ser entero en el punto de salida, para n=0.
Como las cúspides se dibujan cada n/k vueltas, nunca podremos cerrar el ciclo porque n/k solo podrá ser entero en el punto de salida, para n=0.
¿Nunca se cerrará la curva? ¿Habrá infinitas cúspides?
Entonces... ¿cuánto tiempo necesitaríamos para dibujar toda la curva? Dale "vueltas" al tema.
Entonces... ¿cuánto tiempo necesitaríamos para dibujar toda la curva? Dale "vueltas" al tema.
¡Esto es todo! Si has leído hasta aquí, espero que te haya gustado.
Por si te interesa, aquí encontrarás todas las curiosidades que explicamos, ordenaditas y paso a paso: instagram.com/tallynumbers
Por si te interesa, aquí encontrarás todas las curiosidades que explicamos, ordenaditas y paso a paso: instagram.com/tallynumbers
• • •
Missing some Tweet in this thread? You can try to
force a refresh
