Thread by @LargeCardinal

So, something that I've been looking at quite a lot is quantum tech; Seeing what '#quantum' means and setting up @quantum_village; so, I'd like to present this blog on 'breaking XOR with Grover's Algorithm' ! Here's a 🧵👇 for #NerdHour (thx @dcuthbert)
assemblyofsecrets.blogspot.com/2022/01/how-to…

An aside - this blog post has an accompanying @GoogleColab for those who want to play along at home! This code is fairly reusable for examples people might want to try. colab.research.google.com/drive/1Hf32FpC…

So, the aim of this work is to show one method for using Grover's algorithm (the 'other' famous one from Shor's factoring algorithm) to break cryptography... Now, there has been plenty written on this, such as this post from @ibm's @qiskit; qiskit.org/textbook/ch-al…

What is missing is, I think, relevancy. It's one thing to show 'here is some advantage in using quantum computers' and another to show 'here's where that advantage works and what you need!'... There's also some misconceptions to clear up...

One such misconception is that "Grover's search lets you search a telephone directory" and that's just plain wrong, sorry. The sense of the 'search' is over a set of superpositions... But these have to be constructed algorithmically, which a phone book is not!!

(Think of it this way - there is no algorithmic link between "Alan Smith" and "555-XXXX" being Alan's phone number... So Grover's search will not necessarily help you here unless you _create_ a link, which is likely more computationally expensive than the classical search!!)

So what do we do? Well, first let's set the scene... and the Prologue is "WE DON'T NEED TO DO THIS!" To perform this attack, you need a known piece of plaintext and ciphertext, a known plaintext attack...

But because *~-(math)-~* you can extract the key for XOR encryption if you know a ciphertext/plaintext pair... here's some code for this if you want to see how, see hte blog for the maths overview...

So let's setup a Grover's search anyway to 'crack XOR' in the most obscenely overkill way possible... here's the starting arrays; we will show how to get the 'key bits' out the end of this algorithm.

So, there are two phases to Grover's Search - The ORACLE and the DIFFUSER. Let's start with the Oracle, and no we don't mean an AI that hands out cookies to compensate for the enslavement of all mankind...

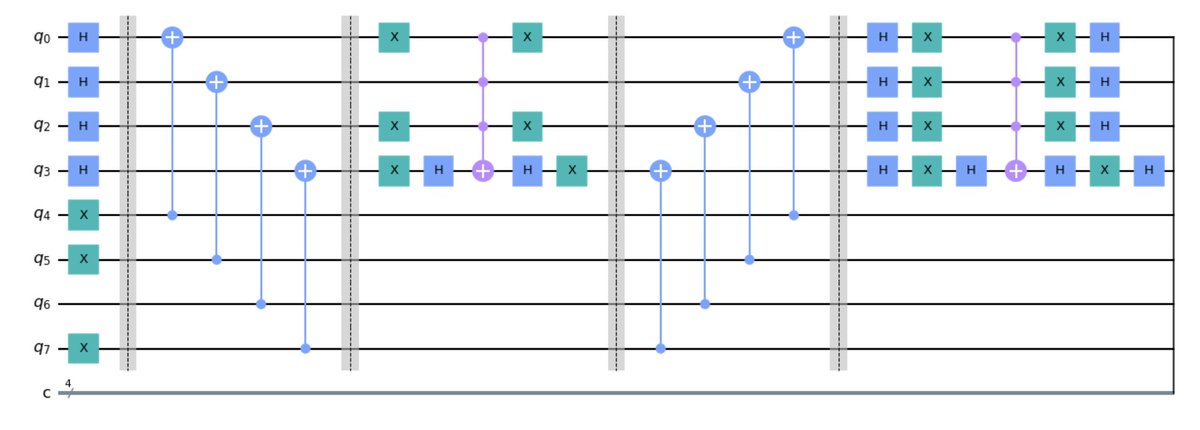
First we setup the input plaintext, and put our 'key' into superposition... this is just 'apply Hadamard, or 'H', gates to all the qubits'... that's generally how you 'go quantum' and add superposition. In circuit diagrams it looks like this:

For those unfamiliar - this is a 'quantum circuit' diagram. The lines are 'qubits', the squares and circles and such as 'gates' (the dotted line is just a 'barrier' to make it look pretty... no, really...). This is the current way we represent quantum algorithms.

Now, recall the plaintext bits in a previous tweet? Well, that is coded on qubits q_4 to q_7... can you see how the '1's become 'X's? That's because the 'NOT' gate, called 'X', is applied to represent a '1' here. The 'H' gates represent 'both 0 and 1 at the same time'.

Now we need to 'encrypt' our plaintext. For XOR there's a neat quirk that the CNOT gate (see the blog for a breakdown) essentially performs an XOR on the non-control qubit. So, that's just what we do - we XOR the plaintext with the superposition'd keys:

It's worth mentioning that we really are, mathematically, encrypting using all possible keys at once!! I mean, that's what superposition in #quantumcomputing means... But what now? We can't meaningfully extract the key... so what do we do? Answer: invert the phase of what we want

Qubits occupy a space that is often approximated by this picture - the Bloch sphere. Whilst we 'measure' (read: output) based on the vertical (for binary based quantum computing), we can actually compute over a 2d surface of a sphere. So we can talk about the 'phase' of a qubit..

..noting that the phase is distinct from the rotation between 'up' and 'down' that defines the probability of a '0' or '1' output respectively. We can use a circuit from Grover's original paper to invert the phase... here's what we do.

We apply a 'controlled-Z' gate... but in IBM we do this by applying an H gate, then a CNOT gate, then a H again. (see qubit q_3). Here we use a multi-control NOT gate, so we have to activate all qubits... we do this with some X gates...

Note that the X gates correlate to the zeroes in the 'ciphertext' array we defined earlier. This is deliberate... it's basically a filter to say 'flip the phase when the encrypted plaintext fills in the gaps on the CNOT gate'. And only one state will do that - the key state!

(for those curious, this is a technique copied from this paper: eprint.iacr.org/2021/554 it's a nifty IACR preprint from July last year)

Ok, so now what do we do? Well, we have to undo the steps to 'balance out' the superposed states, with just one state inverted. How? Well, ot invert a quantum circuit, you just run it backwards. No, really. So the full oracle looks like this:

But why do this? Well, what we have just setup is effectively this (borrowing images from @qiskit's page, linked above); the 'W' state is the key state we want to extract. But how do we extract this?

Well, we use the next part... the DIFFUSER. No, not a tool used in a 'legal state'. It's a nice circuit that takes this setup and rotates it around the average line... note how the average is pulled down by the inverted state? That means the graph will actually look like this:

So you can see how we can find the key!! We just diffuse and run the circuit enough times (because quantum computations are probabilistic) to get this 'spike' out, and we know that's probably the key! So here's what adding the diffuser looks like:

Ok, so we are all setup... but does it run? YES!! And here's the output (you can see for yourself if you run the google colab or download it and run the jupyter notebook locally for yourself :P ) - see how that graph looks very much as it should? It workeD! :D

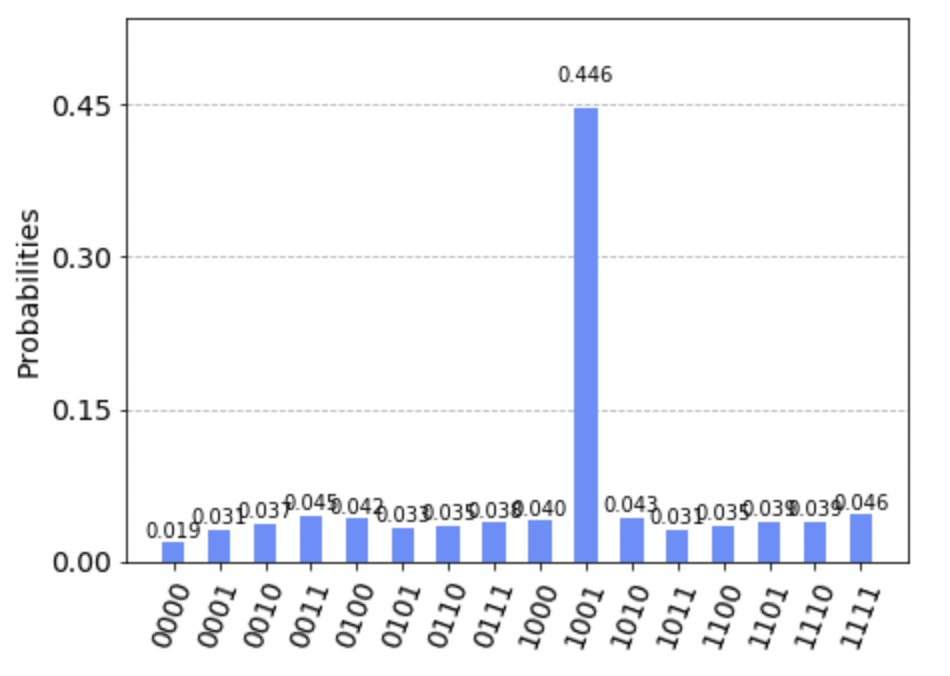
And what was the output? '1001'... which is precisely the key we wanted ! (check the tweet in the thread or just calculate the XOR for yourself :P )

So, that's the 'most useless' Grover's example, but it's fully worked out as an educational/informational example, backed up by code. :)

If you want to learn more, I recommend the @qiskit and @GoogleColab links above. I get a lot of 'but what books?!?' and I usually recommend @jackhidary's book on Quantum Computing - the 2nd edition looks great! amazon.co.uk/Quantum-Comput…

Anyway, that's it for now... happy quantum hacking and see you at @quantum_village! :D