Thread by @svpino

One of the most popular activation functions used in deep learning models is ReLU.

I asked: "Is ReLU continuous and differentiable?"

Surprisingly, a lot of people were confused about this.

Let's break this down step by step: ↓

Let's start by defining ReLU:

f(x) = max(0, x)

In English: if x <= 0, the function will return 0. Otherwise, the function will return x.

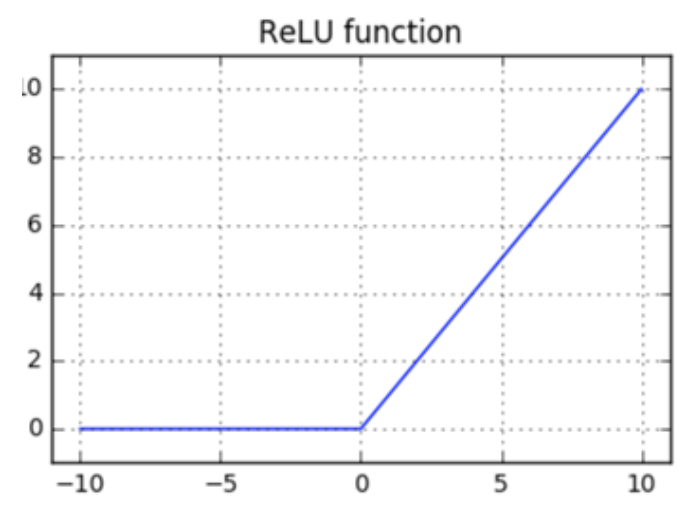
If you draw this function, you'll get the attached chart.

Notice there are no discontinuities in the function.

This should be enough to answer half of the original question: the ReLU function is continuous.

Let's now think about the differentiable part.

A necessary condition for a function to be differentiable: it must be continuous.

ReLU is continuous. That's good, but not enough.

Its derivative should also exist for every individual point.

Here is where things get interesting.

We can compute the derivative of a function using the attached formula.

(I'm not going to explain where this is coming from; you can trust me on this one.)

We can use this formula to see whether ReLU is differentiable.

Looking at ReLU's chart again, the interesting point is when x = 0.

That's where the function changes abruptly.

If there's going to be an issue with the function's derivative, it's going to be there!

Here is the deal:

For ReLU to be differentiable, its derivative should exist at x = 0 (our problematic point.)

To see whether the derivate exists, we need to check that the left-hand and right-hand limits exist and are equal at x = 0.

That shouldn't be hard to do.

Going back to our formula:

The first step is to replace f(x) with ReLU's actual function.

It should now look like this:

So let's find out the left-hand limit.

In English: we want to compute the derivative using our formula when h approaches zero from the left.

At x = 0 and h < 0, we end up with the derivative being 0.

We can now do the same to compute the right-hand limit.

In this case, we want h to approach 0 from the right.

At x = 0, and h > 0, we will end up with the derivative being 1.

Awesome! This is what we have:

1. The left-hand limit is 0.
2. The right-hand limit is 1.

For the function's derivative to exist at x = 0, both the left-hand and right-hand limits should be the same.

This is not the case. The derivative of ReLU doesn't exist at x = 0.

We now have the complete answer:

• ReLU is continuous
• ReLU is differentiable

But here was the central confusion point:

How come ReLU is not differentiable, but we can use it as an activation function when using Gradient Descent?

This was the reason many people thought ReLU was differentiable.

What happens is that we don't care that the derivative of ReLU is not defined when x = 0. When this happens, we set the derivative to 0 (or any arbitrary value) and move on with our lives.

A nice hack.

In deep learning, it's rare for x to be precisely zero. We can get away with our hack and not worry too much about it.

This is the reason we can still use ReLU together with Gradient Descent.

Isn't math beautiful?