#Subdivision schemes don't only help finite element methods. In a recent paper, we present a #mathart application of creating #weaving patterns from said schemes. Furthermore, we extent these patterns to create a #jigsaw puzzle. Here's a thread.🧵1/13 doi.org/10.1080/175134… 

Computer simulations for, e.g., the weather, solve complex problems on a 2D domain. They mostly do so by splitting the domain into a finite set of smaller and simpler elements on which the simulation can be run fast and efficiently. This uses subdivision schemes. 2/13 
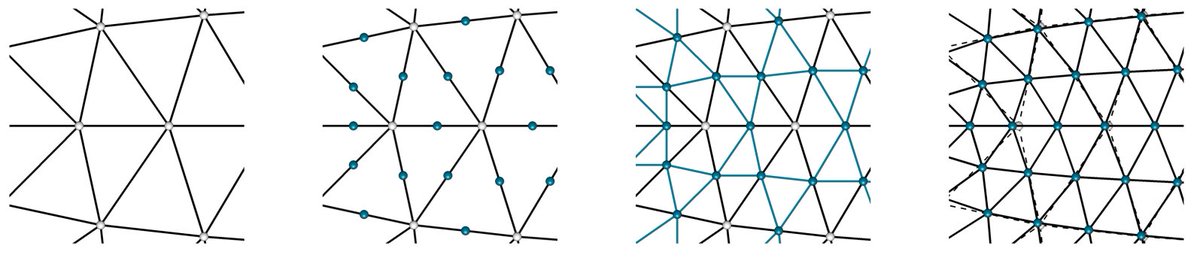
If the output domain should be triangles, there is the Loop subdivision (see image from previous tweet), the butterfly🦋 scheme, or the √3 scheme. For output made of quadrilaterals, use mid-edge, Doo-Sabin, or Catmull-Clark. Irregular input gives irregular output, though. 3/13 

None of these schemes create pentagonal faces. We discuss a procedure where, by replacing each edge by a Z-shaped triplet of edges and connecting their vertices to face-midpoints, the output mesh becomes a mesh purely comprised of pentagonal faces. 4/13 

Applying this subdivision leads to non-convex pentagons. Thus, we perform a smoothing step, moving vertices towards the barycenter of their original faces. Whether or not this operation keeps the faces convex for all inputs and arbitrary many subdivisions is an open problem. 5/13 

A first #mathart object arises when considering repeated pentagon snub subdivisions of an initial, regular pentagon. In this case, the boundary curve subdivides to a #fractal curve. Whether or not inner curves form fractals given the smoothing is an open problem. 6/13 

As mentioned, repeatedly applying the pentagon snub subdivision scheme to a regular pentagon does not only yield a #fractal curve on the outer boundary, but also fractal-like #mathart curves inside the mesh. These arise both from edges as well as from the remaining faces. 7/13 

From the subdivision, we can create a #weaving by removing each middle edge of the introduced Z-triplets, i.e., gluing two pentagons together. A strand of the weaving is given by those tiles whose tips are connected by a now absent middle edge of a Z-triplet. 8/13 
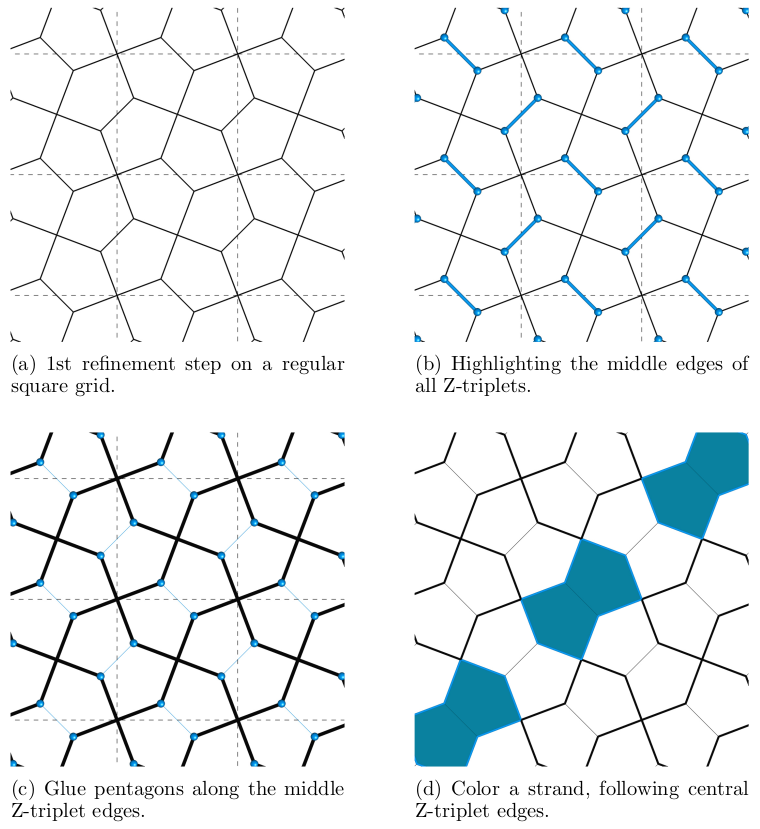
An interesting phenomenon arises when observing a strand of the #weaving #pattern under a subdivision operation. The strand splits into two new strands, which are intertwined. This also holds for an additional operation, giving four strands in total that form pairs. 9/13 

The described #weaving #pattern now leads to a #mathart activity: Given the square or the regular pentagon and some simple paper cutouts, we can build the weaving by hand. Find the necessary templates attached to this tweet and give it a try! 10/13 







In the fifth and second-to-last chapter of the paper, we discuss how the #weaving #pattern can be generalized to other subdivision schemes, such as the aforementioned scheme by Loop. Here, subdividing strands gives two parallel, not intertwined strands. 11/13 

For our final piece, we realized one of the subdivisions as a #jigsaw #puzzle, much in the spirit of @nervous_system. The two sides of the puzzle illustrate the strands by showing them as line segments or rather by coloring in the glued mesh faces. 12/13 



Our work is #OpenAccess in @MathsArts, thanks to the support by @tudelft. Thanks to my co-authors for a great collaboration, to the editors @Gelada and @henryseg, and to @dfg_public for supporting my research conducted at @TUDelft_CGV. Full article: tandfonline.com/doi/full/10.10… 13/13
• • •
Missing some Tweet in this thread? You can try to
force a refresh




