A very simple and fairly generic way to build confidence set when the distribution of your data is known. 👇🏿 

This is not usable in practice, but we can try to approximate the distribution of the data empirically. The resulting confidence set is what we call "conformal prediction set" 👇🏿 

The above construction induces a conformity/typicalness function that takes low value on the variables unlikely to come from our distribution 👇🏿 

Well nice! But it quite hard/impossible to compute the conformal set in general. For regression problem, it requires to fit a predictive model infinitely many times 👇🏿 

There is a very easy way to get around the problem. You just have to use our good old technique of data splitting 👇🏿 

We can also try to exploit more data à la K-fold cross-validation, in order to reduce the size of the confidence set. But it usually affects the statistical guarantee 👇🏿 

Can we simultaneously overcome all this issue? My answer is yes as long as the prediction model is stable 👇🏿 

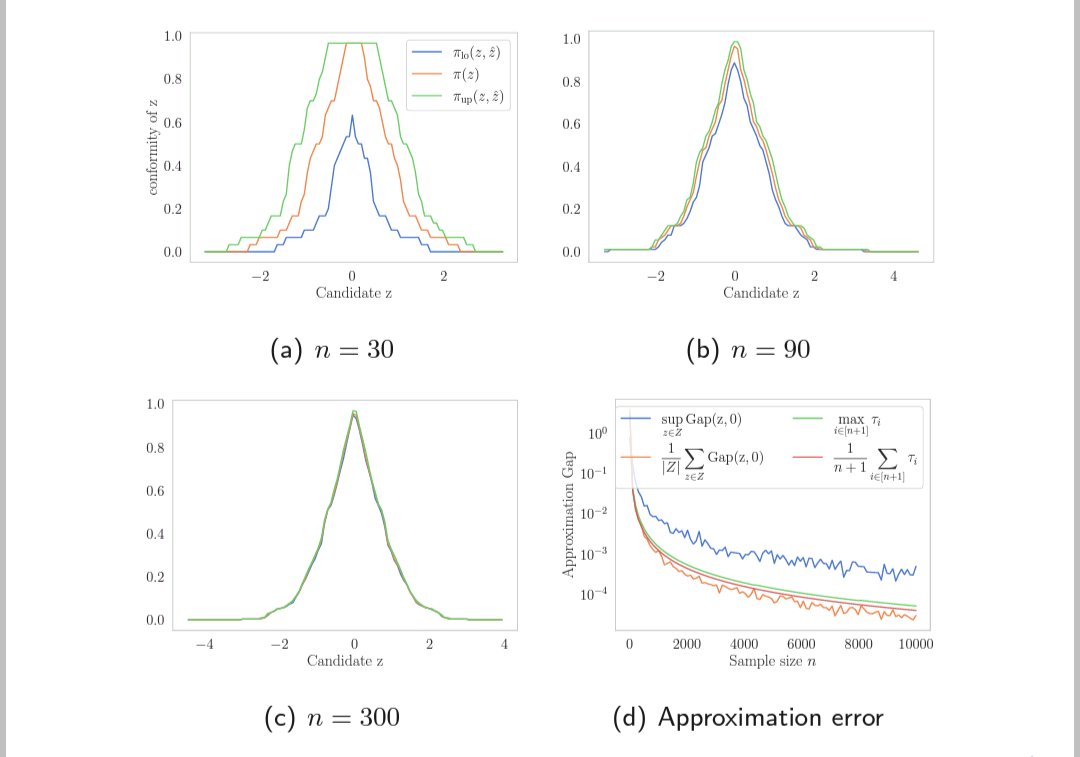
The strategy is to merely sandwich the conformity function with an easier the compute one: fit your model once and for all and leverage stability bounds to control de deviation 👇🏿 

Here is what it looks like numerically. We recover the conformal set quite tightly depending on how stable your model is. Bonus: you can compute the approximation gap for free.
😉 See you at my talk/poster for more details/collaborations 🙌🏿
😉 See you at my talk/poster for more details/collaborations 🙌🏿
• • •
Missing some Tweet in this thread? You can try to
force a refresh






