Thread by @periodistan_

Pitágoras, Gauss, Ruffini, Fibonacci...
Todos los matemáticos que vemos en la secundaria son europeos.
Se nos enseña la matemática como si fuese una ciencia occidental.

Creeme: después de este hilo, tu vida va a cambiar.

1) Nuestro sistema educativo está profundamente influenciado por los valores europeos.
Tiene lógica: colonizados por España, dentro del mundo occidental...

El tema es que, durante nuestro aprendizaje, no vemos casi nada por fuera de ello: se nos cierran así millones de puertas.

2) Un ejemplo.
Entre secundaria y universidad, estudié muchísimas veces Revolución Francesa y Revolución Industrial. Todas las fechas, todos los detalles.
Y nunca jamás leí algo sobre Brasil. Nunca, eh.

Un país gigante, vecino, 200 millones de habitantes: al parecer, no existe.

3) Si esto sucede con Brasil, imagínense con África, Asia...
La historia de África "termina" en las Pirámides.
La historia de Asia "termina" en Babilonia.
¿América Central? Hasta los mayas.

¿Quién inventó la imprenta? Obvio, Gutenberg.
¿Quién inventó el papel? No sé, un chino...

4) Que todos conozcan a Gutenberg y nadie a Cai Lun -mucho más importante- habla a las claras de este eurocentrismo.
Además, ¿Cómo vamos a saber el nombre de un chino? ¡No tienen nombre!

¿Quién inventó la telegrafía sin hilos? Marconi.
¿El cine? Lumiere.
¿La pólvora? Los chinos.

5) Así, "los chinos" serían como un sujeto colectivo indiferenciado, una masa amorfa de 1.300 millones de habitantes iguales entre ellos y sin personalidad propia.
"Los árabes", "los indios"...

La astronomía es otro grandísimo ejemplo de todo lo que estoy diciendo.

6) Piensen ya mismo en dos astrónomos, los primeros que se les vengan a la mente. Ahora.
¿Listo?
OK, Galileo y Copérnico.
¿Física?
Newton, Einstein...

En el año 499, Aryabatha ya hablaba de una fuerza similar a la gravedad. No lo conoce nadie en nuestros países. Por indio.

7) Voy a volver a las matemáticas. Y como India es el país en el que me encuentro, orientaré el hilo en los descubrimientos matemáticos indios.
Pero podría haber sido sobre China, el mundo árabe, Persia, etc.

Total, todo lo que no es Europa lo desconocemos.

8) En India, por arrancar, se empezaron a utilizar los números que hoy conocemos como arábigos (pero que llegaron a Arabia, y de ahí a Europa, desde el Indostán).
La superioridad de estos símbolos es abrumadora.

En números romanos, tenías que escribir: MMMCMXCIX.
En India: 3999.

9) Sigamos.
Los números creados en India -con influencia también china- iban, en un principio, del 1 al 9.
Faltaba algo.
El cero.

Y se inventó en India.
Allí, hace más de un milenio, se llegó a la conclusión de que el cero no era el vacío: era un número por derecho propio.

10) La revolución del cero es una de las grandes revoluciones de la historia.
¿Por qué?

Porque permite crear números enormes y así, aumenta de forma inimaginables los alcances prácticos de la matemática.
¿Cómo escribís diez millones con una M, una X, una L?
En cambio: 10000000.

11) El actual sistema numérico que usamos, derivado de la India, es un sistema decimal y posicional.
¿Qué quiere decir esto?
Que las cifras adquieren su valor dependiendo de la posición.

En 123, el 1 vale 100.
En 21, el 1 vale 1.
En el sistema romano, una X es siempre una X.

12) Ya mencioné al pasar a Aryabatha. Volveremos a él. Pero vayamos ahora a otro genio de la historia: Brahmagupta. Siglo VI.
¿Tampoco lo habías escuchado nunca?

Pero sí hiciste un montón de cuentas gracias a sus reglas, que son las siguientes:
1 + 0 = 1
1 - 0 = 1
1 x 0 = 0

13) En la India de hace 1.500 años, un matemático establecía así las reglas de cálculos con cero que seguimos usando hasta hoy.
Pero había un problema: la división.
¿Qué pasa si hacemos 1 dividido cero?
¿Qué número multiplicado por cero da 1?

Durante seis siglos, nadie lo supo.

14) La respuesta vino desde...India.
Bhaskara II.
Una de las mentes más brillantes que habitó este planeta.
«Uno dividido cero es igual a infinito», dijo.
¿Por qué?
Porque para alcanzar la unidad se debe recurrir siempre a un divisor fraccional más y más y más pequeño = ♾

15) Muchos de los descubrimientos indios tal vez haya que analizarlos en el trasfondo de su sociedad.
En el hinduismo, el concepto de la eternidad, de la nada y la ausencia de materia es recurrente: todo el tiempo se vuelve a él.

¿Tendrá que ver con la invención del cero?

16) La leyenda dice que Bhaskara había estudiado el horóscopo de su hija, como es costumbre hasta hoy en India para arreglar casamientos.

Y había visto algo terrible.
Si la primera relación sexual entre ella y su marido no sucedía a una determinada hora, él fallecería pronto.

17) Entonces, colocó una taza con un pequeño agujero, que él había hecho, en una fuente con agua.
Le dijo a su hija: "Sólo empiecen cuando la taza se haya hundido".
Pero ella se acercó a ver, y un aro se le cayó en la taza, afectando el cálculo.

Al poco tiempo, enviudó...

18) Bhaskara, tristísimo, escribió un libro para enseñar matematica.

Los problemas eran estos:
"La raíz cuadrada de la mitad del número de abejas en un enjambre ha volado hasta la planta de jazmín.
Ocho novenos del enjambre atrás quedaron.
Dime, encantadora dama, cuántas son".

19) Bhaskara inventó la fórmula para resolver ecuaciones cuadráticas. La llamada "resolvente".
Seguro la usaron en el secundario: a mí me costaba mucho: equis igual menos be más menos...

¿Por qué no nos la enseñan como la fórmula de Bhaskara? Simple: porque la inventó un indio.

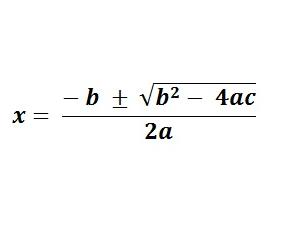
20) Volvamos a Brahmagupta. Porque si el cero fue una revolución, la de los números negativos directamente rompió todo.
5 - 4 = 1
5 - 5 = 0
Pero... ¿5 - 6?
Fue él, siglo VI, el que consideró por 1ra vez las propiedades de los números negativos.
Esto que hizo cambió el mundo.

21) ¿Para tanto?
Sí, porque al empezar a calcular con números negativos, la matemática adquiere un carácter abstracto.
Antes, era: tengo ocho monedas, me dan cinco, ahora tengo trece.
La matemática se veía: eran objetos.

Pero, ¿Cómo se puede ver en la realidad un menos catorce?

22) Al salir del mundo material y entrar en el terreno de lo abstracto, las posibilidades matemáticas se incrementan en forma exponencial. Son las matemáticas que conocemos hoy.

Y si hay un país en que la inmaterialidad es importante -yoga, meditación, ascetismo- ese es India.

23) ¿Todo esto les voló la cabeza?
Y es solamente la primera parte. Vendrá una más, con otras figuras increíbles y desconocidas.

Yo no prometí una primicial mundial. Apenas prometí un hilo, y acá lo tienen.
Por hoy me despido, desde la "numeraria" India.

X = Periodistán😏