Thread by @dlouapre

My paper with Stuart Bartlett on "Provenance of Life" is finally out in @PhysRevE ! We simulated a simple chemical system, and showed its ability to learn by association, and use this defend itself against a threat.
A thread🧵#astrobiology #OriginOfLife
doi.org/10.1103/PhysRe…

It all started when Stuart and Michael Wong @miquai proposed a new broader definition for "life". They wanted to cover not only life as we know it on Earth but also "as it could be elsewhere in the Universe". They called this new concept "LYFE".
doi.org/10.3390/life10…

Their definition is based on 4 pillars :
* Dissipation
* Auto-catalysis
* Homeostasis
* Learning.
The first three pillars imply that to be considered « alive », a system should be able to dissipate free energy, self-replicate, and maintain its internal balance.

The 4th pillar requires that a living system should be able to *learn* from its environment in order to improve its long term survival.
Darwinian evolution by natural selection is one possible such learning mechanism, but as we will see it’s not the only one !

In their paper, Stuart & @miquai mentioned several systems exhibiting one or more of those four pillars. For instance a wildfire exhibits dissipation and auto-catalysis, but lacks homeostasis and learning.

Among those "almost living" systems, a fascinating example is the Gray-Scott reaction-diffusion system. It’s a fairly simple chemical reaction capable of dissipation, homeostasis, and a spectacular form of autocatalysis : self-replicating spots !

Stuart had already extensively studied that system, and realized that it only lacks one pillar of Lyfe : LEARNING... and this is what he proposed me to investigate !
After some hard work, we finally report our findings in that paper we just published together in Phys. Rev. E.

Let’s start from the Gray-Scott reaction-diffusion system. It is a simple chemical system involving two species (A and B) that are able to diffuse in a 2D medium. They can react following an autocatalytic reaction : A + 2B => 3B.

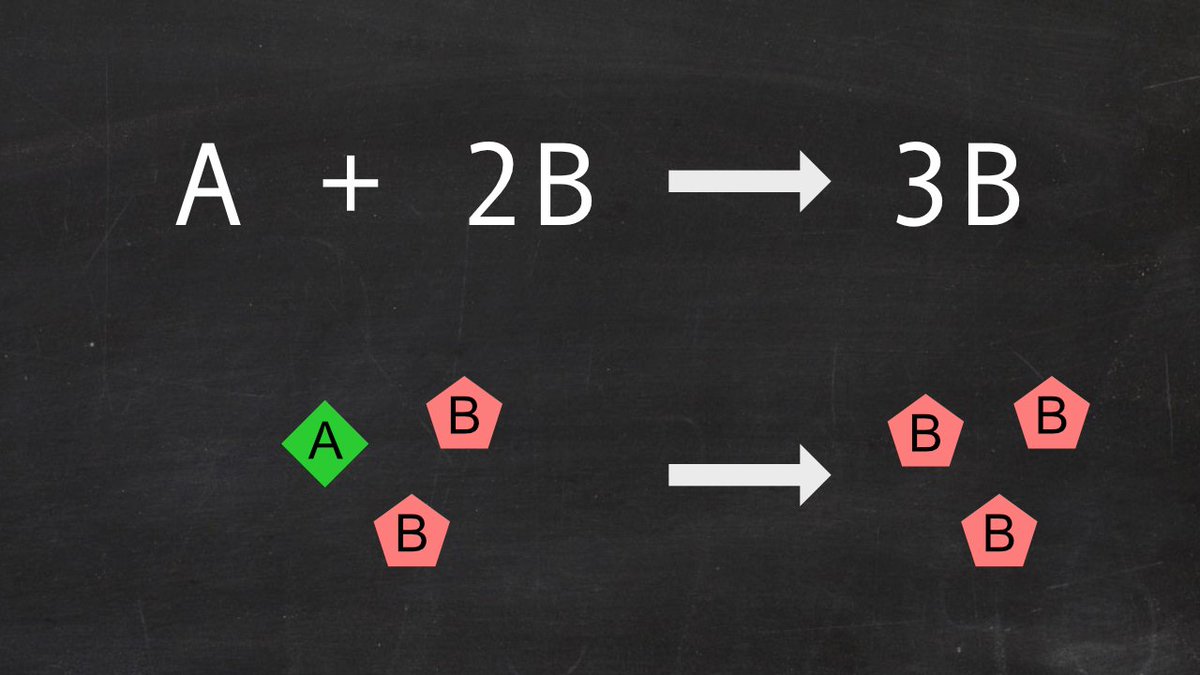
You can think of compound B as « the (living) stuff », and A as « the fuel ». B constantly degrades, but auto-catalysis replaces it locally, while the « fuel » A is continuously replenished everywhere. Below are the corresponding differential equations for concentration

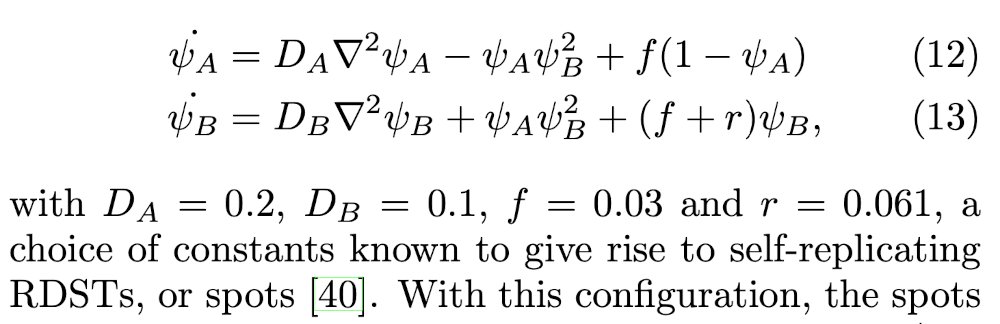
With a proper choice of reaction constants and initial random concentrations, when we plot the concentration of B, we can see self-replicating spots invading the available space. Beautiful !

When the system finally reaches what looks like a stationary state, it is actually maintained out of equilibrium by the combination of B degrading and being regenerated by autocatalysis.
Ok, but now how do you add "LEARNING" to such a chemical system ?

The type of learning we considered is called ASSOCIATIVE LEARNING. This is well illustrated with the famous example of Pavlov’s dog. The dog is repeatedly presented a stimulus (the bell) followed by an event (food).

The dog learns the association between the stimulus and the event, so it ends up salivating as soon as the bell rings.
In that case, learning such an association does not really help survival, but associative learning might also be what happens for some preys and predators.

For instance a gazelle might learn to recognize a stimulus (visual, auditory, olfactive…) as announcing a cheetah. Learning such an association allows preemptive reaction (escaping in that case) which improves survival.

So far, I’ve used animals with highly complex nervous system to illustrate associative learning. But could you also get it with a simple chemical system made of a bunch of chemical species ?
First we needed to devise a situation that would be similar to the prey-predator case.

Let’s consider a compound T (for toxin) that can destroy the B compound of the Gray-Scott system (remember B is the « stuff » the replicating spots are made of).
Let’s assume this toxin T is regularly delivered to the system (as periodic boluses of a certain concentration).

Here is an example where toxin T is delivered on the boundaries of the system. (right panel, concentration of T is in red)
We can see it progressively destroys the spots and hence « kills » our system.

Now let’s suppose every bolus of toxin T is preceded by a bolus of another chemical species S (S for Stimulus) occuring slightly before.
Being able to learn the association between the occurence of S and T would help the system to defend itself by anticipation !

For instance if our system is able catalyze the production of an antidote N which can neutralize toxin T, it would be more efficient to produce N as soon as the stimulus occurs (rather than waiting for T to be delivered.)
Learning the association between would improve survival !

Now the system must be able to learn but also unlearn. If the association between S and T changes or disappears (say S still occurs but no more T follows), we want to stop producing the antidote. Such a spurious production of N might be detrimental or simply wasting ressources.

So what we want to learn is actually the *strength* of the association between stimulus and toxin. It is a parameter from the environment defined as the ratio between the bolus concentrations of Toxin and Stimulus.

We assume that this environmental parameter (we called epsilon) can slowly vary over time, and we want our chemical network to be able to adapt to it, by continuously learning and updating the strength of the association between stimulus and toxin.

For this, we created a benchmark situation where this parameter epsilon is slowly rising, reaches a peak, then decreases and finally stays at zero (so that at the end, no more toxin is delivered while the stimulus still occurs).
(see figure below from our paper)

So can we create a chemical system that can learn and survive such a situation ?
First we studied the problem in "0 dimension", that is without diffusion, by assuming a well-stirred medium where all concentrations are homogeneous.

To create an « associative learning » chemical network, we considered two new compounds M and L acting respectively as short and long term memories. M is catalyzed by the presence of stimulus S but quickly decays. Its role is thus to register the recent occurence of the stimulus.

Long term memory L is then catalyzed from short term memory M by the presence of toxin T. So L increases when a toxin bolus occurs shortly after a stimulus bolus. L slowly decays but overall it registers the temporal association between the stimulus and the toxin (in that order)

Simulating this chemical network, we’ve shown that the concentration of L correlates very well with the strength of the association between S and T (the environmental parameter epsilon), and captures its long term variations.
(Figure 4 from the paper)

The presence of L can then be used to trigger the production of an antidote N everytime the stimulus S occurs. This acts as an anticipated premptive reaction to the (future) occurence of toxin T and helps the survival of the system.

If we consider an environmental parameter that has complex variations, we can see that the concentration of long term memory L still closely follows it.
Our simple system is able to learn a continuous parameter from its environment, and have an internal representation of it !

That was for the 0-dimensional case ! We then tried to include this learning chemical network into the Gray-Scott reaction-diffusion system...and showed it works !
We tested two conditions : toxin delivered everywhere in the medium, and on the boundary only.

In both cases, the system is able to learn the strength of the association, defend itself to stay alive, and reconquer space once the association has disappeared.
(Movie below is for the boundary delivery case)

With this, we have a fairly simple chemical system, exhibiting dissipation, autocatalysis, homeostasis, and a (minimal) form of associative learning helping the long term survival of the system. The four pillars of Lyfe !

Of course, our work is just a simulation, and the next step would be to implement it in a real chemical system (as it has already been done with the Gray-Scott reactions).
We are working on it with our experimental collaborators !

On the simulation side, we have plenty of ideas to push the system further and make it more resilient, more versatile. I'll release the source code very soon !

I'll also make a video on "Science étonnante" to tell the story for my french audience. In the meantime you can watch the video abstract and the video showing all simulations

Tagging a few people that have heard of this work, seen part of it, or might just be interested by this thread @Ironmely @sina_lana @gregeganSF @miquai @artemyte @SilviaHoller2 @ALifeConf @garydagorn @CyrilleVan @ThomasCabaret84