Thread by @neumann_oren

Do #RL models have scaling laws like LLMs?
#AlphaZero does, and the laws imply SotA models were too small for their compute budgets.
Check out our new paper:
arxiv.org/abs/2210.00849
Summary 🧵(1/7):

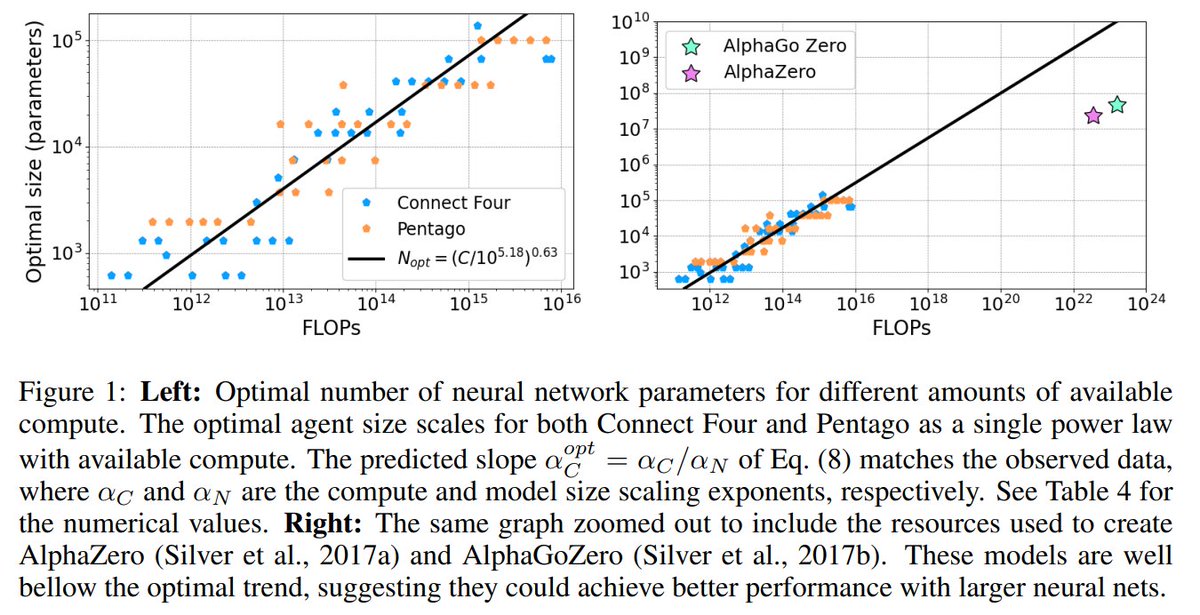
We train AlphaZero MLP agents on Connect Four & Pentago, and find 3 power law scaling laws.
Performance scales as a power of parameters or compute when not bottlenecked by the other, and optimal NN size scales as a power of available compute. (2/7)

When AlphaZero learns to play Connect4 & Pentago with plenty of training steps, Elo scales as a log of parameters. The Bradley-Terry playing strength (basis of Elo rating) scales as a power of parameters.
The scaling law only breaks when we reach perfect play. (3/7)

Playing strength scales as a power of compute when tracing the Elo of optimal agents.
This agrees with previous work by @andy_l_jones :
arxiv.org/abs/2104.03113
Both size and compute scaling laws have the same powers for Connect4 and Pentago. (4/7)

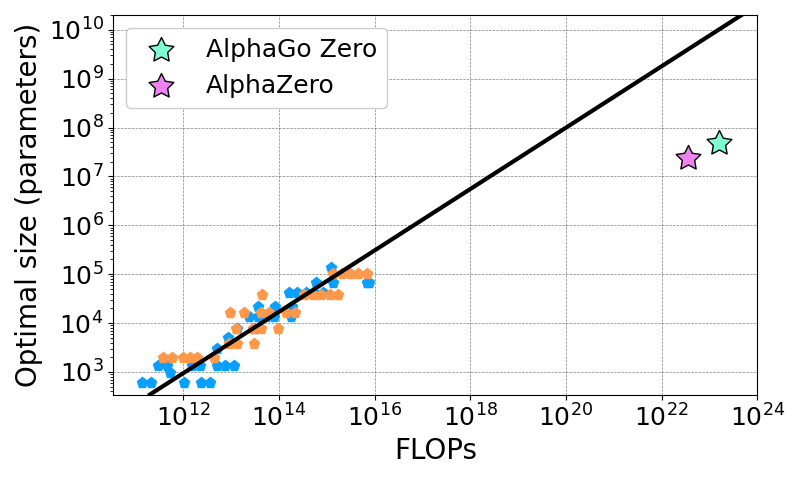
Combining both scaling laws we get a scaling law for the optimal model size with compute. @DeepMind 's AlphaGo Zero and AlphaZero stand far below the optimal curve, using small NNs compared to the compute spent training them. (5/7)

It's easy to see why: Like with LLMs, we find optimal training should stop long before convergence, unlike SotA models that have long training tails. The old ML tradition of training to convergence is wasteful. (6/7)

We believe other RL scaling laws are out there. Check out the paper for an explanation why MARL scaling laws may have been missed before (TL;DR: Elo is logscale). (7/7)