
How Uniswap V3 works, visually 🧵
I had difficulty understanding some of the Uni-v3 tutorials out there, so I’ll try to explain how concentrated liquidity works visually and by using a simple example. I'll assume you have an understanding of Uni-V2, which is much simpler.
I had difficulty understanding some of the Uni-v3 tutorials out there, so I’ll try to explain how concentrated liquidity works visually and by using a simple example. I'll assume you have an understanding of Uni-V2, which is much simpler.
1/
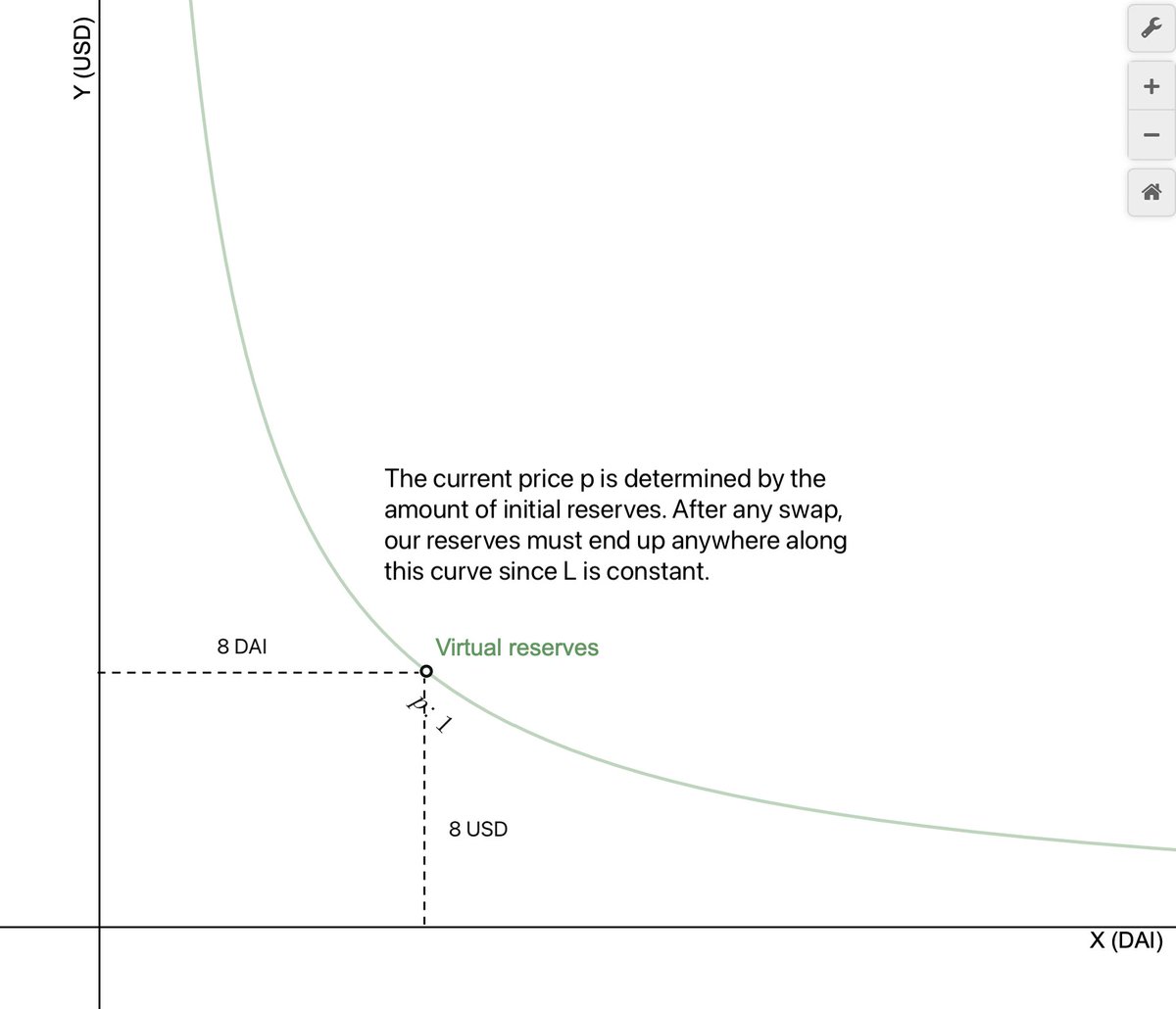
In our example, we’ll be trading a USD($)/DAI pair which has a current price of 1$/DAI.
In Uni-V2, the LP wants to provide equivalent amounts of DAI and USD into the pool, let’s say 8$ and 8DAI.
This curve shows the familiar xy=L^2 curve
In our example, we’ll be trading a USD($)/DAI pair which has a current price of 1$/DAI.
In Uni-V2, the LP wants to provide equivalent amounts of DAI and USD into the pool, let’s say 8$ and 8DAI.
This curve shows the familiar xy=L^2 curve
2/
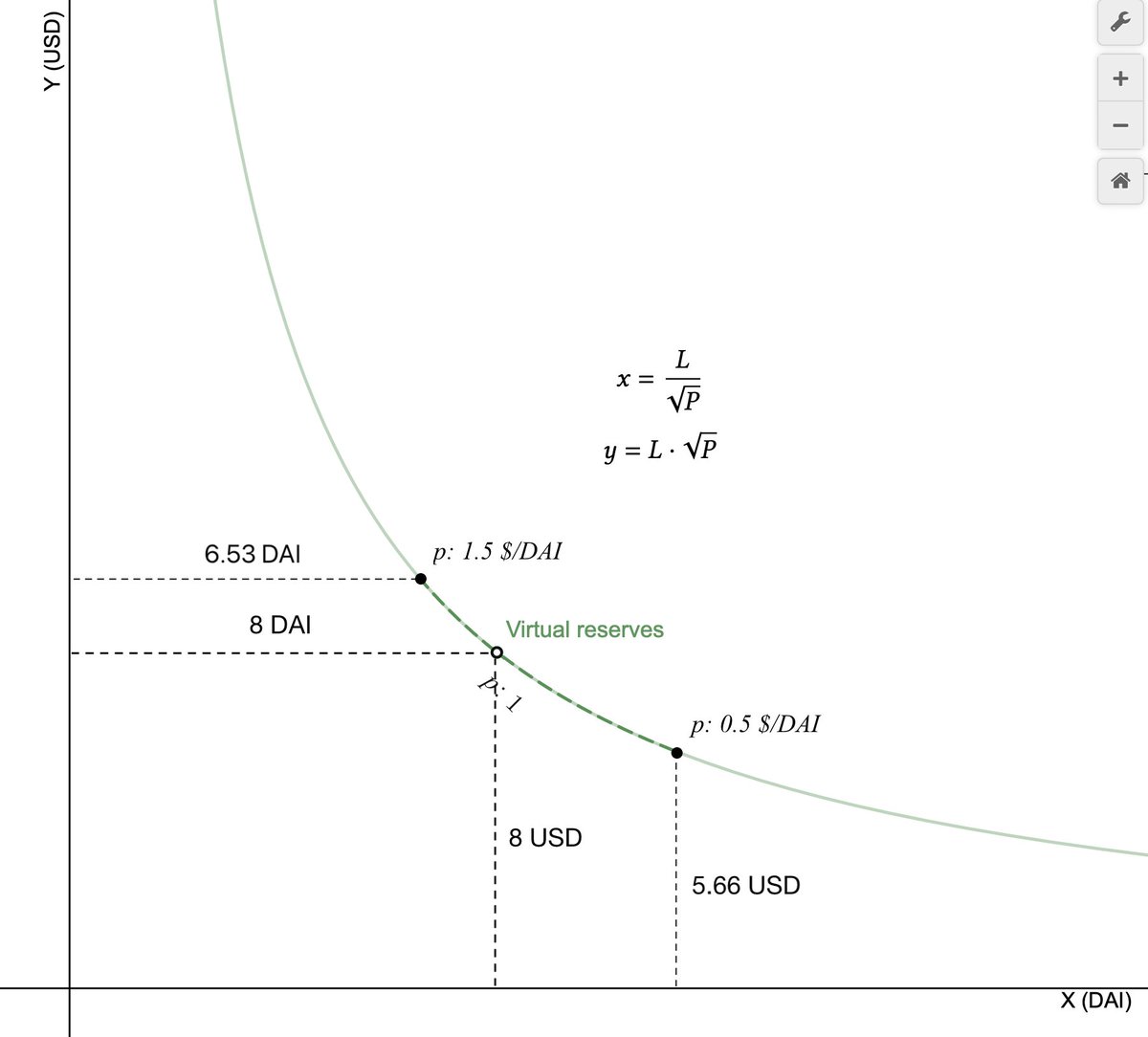
In UNI-v3, our LP wants to provide liquidity in a price range of 0.5$/DAI and 1.5$/DAI, but how much USD and DAI do they need to provide for the equivalent L=8?
Since we are bounding the price range, we only need to support the dashed part of the virtual reserves curve.
In UNI-v3, our LP wants to provide liquidity in a price range of 0.5$/DAI and 1.5$/DAI, but how much USD and DAI do they need to provide for the equivalent L=8?
Since we are bounding the price range, we only need to support the dashed part of the virtual reserves curve.

3/
We can calculate the amount of reserves given L=8 and the price. When the price is 1.5$/DAI, there is 6.53DAI remaining. This means we only actually need
8-6.53=1.47DAI of DAI reserves.
Similarly, when the price 0.5$/DAI, we only use
8-5.66=2.34$ of USD reserves.
We can calculate the amount of reserves given L=8 and the price. When the price is 1.5$/DAI, there is 6.53DAI remaining. This means we only actually need
8-6.53=1.47DAI of DAI reserves.
Similarly, when the price 0.5$/DAI, we only use
8-5.66=2.34$ of USD reserves.
4/
Here, the concentrated liquidity curve is labeled real reserves. It’s the same curve as before but shifted down and to the left. Beyond our price range, it would require negative reserves, so swaps can’t happen past those points. p2 shows our initial deposit calculated earlier
Here, the concentrated liquidity curve is labeled real reserves. It’s the same curve as before but shifted down and to the left. Beyond our price range, it would require negative reserves, so swaps can’t happen past those points. p2 shows our initial deposit calculated earlier

5/
Now, let’s add another LP#2. They would like to deposit with a price range of 0.8$/DAI - 2$/DAI with L=4.
The pictures show two real reserve curves, one for each LP. The upper right diagram plots L as a function of log(price). Remember L is constant in the price range.

Now, let’s add another LP#2. They would like to deposit with a price range of 0.8$/DAI - 2$/DAI with L=4.
The pictures show two real reserve curves, one for each LP. The upper right diagram plots L as a function of log(price). Remember L is constant in the price range.


6/
To get the market making curve for our pool, we add these curves together. The red squares represent liquidity contributions from LP#1 and orange for LP#2.
Note that for certain price ranges L is constant, ex: between .8 and 1.5 $/DAI, both LPs are active so L=8+4=12.


To get the market making curve for our pool, we add these curves together. The red squares represent liquidity contributions from LP#1 and orange for LP#2.
Note that for certain price ranges L is constant, ex: between .8 and 1.5 $/DAI, both LPs are active so L=8+4=12.



7/
Now, someone wants to buy 3$ worth of DAI. How much DAI do they get? We can’t just plug into a formula because the MM curve is piecewise as shown above. However, each piece has a constant L.
In our example, we can split this into two steps, one for each piecewise curve.
Now, someone wants to buy 3$ worth of DAI. How much DAI do they get? We can’t just plug into a formula because the MM curve is piecewise as shown above. However, each piece has a constant L.
In our example, we can split this into two steps, one for each piecewise curve.
8/
In the first calculation, in blue, we can calculate the input/output amounts using just L and the start/end price of the section.
The second calculation, in pink, requires calculating the end price first, and then using the same formulas in the first calculation.
In the first calculation, in blue, we can calculate the input/output amounts using just L and the start/end price of the section.
The second calculation, in pink, requires calculating the end price first, and then using the same formulas in the first calculation.

9/
There are many other nuances to the Uni-V3 implementation, namely that an LP can’t arbitrarily set the price range, the boundary must fall on a price tick.
And since the number of piecewise curves is indefinite, the implementation must be done iteratively.
There are many other nuances to the Uni-V3 implementation, namely that an LP can’t arbitrarily set the price range, the boundary must fall on a price tick.
And since the number of piecewise curves is indefinite, the implementation must be done iteratively.
10/
Hope this helped you better understand Uni-v3. If it did, please tell me, so I know people find it useful. Follow if you’re interested in learning about DeFi and for updates on an innovative AMM launching soon.
Hope this helped you better understand Uni-v3. If it did, please tell me, so I know people find it useful. Follow if you’re interested in learning about DeFi and for updates on an innovative AMM launching soon.
11/
Huge props to the genius that created this chart in desmos, one of the best tools for understanding Uni-v3: desmos.com/calculator/odu…. If anybody knows who it is please tag them.
Perhaps @danrobinson?
Huge props to the genius that created this chart in desmos, one of the best tools for understanding Uni-v3: desmos.com/calculator/odu…. If anybody knows who it is please tag them.
Perhaps @danrobinson?
Tagging some folks who have inspired me
@BarryFried1
@ProgrammerSmart
@haydenzadams
@finematics
@ThorHartvigsen
@korpi87
@_Dave__White_
@tarunchitra
@DazaiCrypto
@PatrickAlphaC
@DefiIgnas
@DeFi_Dad
@DAdvisoor
@resdegen
@Uniswap
@thedefiedge
@BarryFried1
@ProgrammerSmart
@haydenzadams
@finematics
@ThorHartvigsen
@korpi87
@_Dave__White_
@tarunchitra
@DazaiCrypto
@PatrickAlphaC
@DefiIgnas
@DeFi_Dad
@DAdvisoor
@resdegen
@Uniswap
@thedefiedge
https://twitter.com/nutstasher/status/1583345837236572161?s=20&t=mCEHkcRHEAQpklp1uLwHvA
• • •
Missing some Tweet in this thread? You can try to
force a refresh




