Thread by @SalomonCrypto

(1/25) Cryptographic Innovation: Verkle Trees

@ethereum is the World Computer; born a rudimentary number cruncher, on a journey to (inevitably) becoming the dominant global settlement layer. And soon, Ethereum will outgrow the Merkle tree.

Tomorrow's solution: Verkle Trees

(2/25) We begin with a hash function, which transforms an arbitrary dataset into a unique, fixed-length string. A good hash function is irreversible and creates outputs that are indistinguishable from random data.

Think of a hash like a serial number for data of any kind/size.

https://twitter.com/SalomonCrypto/status/1567541750151151616

(3/25) Merkle Trees are made by successive rounds of hashing.

All the data begins on the bottom row (leaf nodes). Then they are grouped together and fed into a hash function. These hashes are grouped (same size) and hashed again, continuing until there is a single (root) node.

https://twitter.com/SalomonCrypto/status/1567638108937801728

(4/25) The purpose a Merkle tree is enable Merkle proofs, which allow verification that a piece of data exists in the underlying dataset (leaf nodes) without transmitting the entire dataset.

This has profound implications for both privacy and bandwidth requirements.

(5/25) The privacy aspects aren't useful for this discussion, but they are worth nothing.

Merkle proofs can verify a piece of data without having to articulate the entire dataset. You do need component pieces of the Merkle tree, but these are just (non-sensitive) hashes.

(6/25) We are here for the bandwidth implications.

Let's say you want to post a ton of data. No one is interested in all the data, and every one has access to Merkle proofs generation (big assumption).

Instead of posting the entire dataset, you can just post the Merkle root.

(7/25) Don't get me wrong, a Merkle proof is significantly more efficient than naïve approach... but it has its limits.

Tl;dr Merkle proofs scale much less quickly than dataset size, but they still scale proportionally. Eventually proofs will outgrow bandwidth capacity.

https://twitter.com/SalomonCrypto/status/1586391080727064577

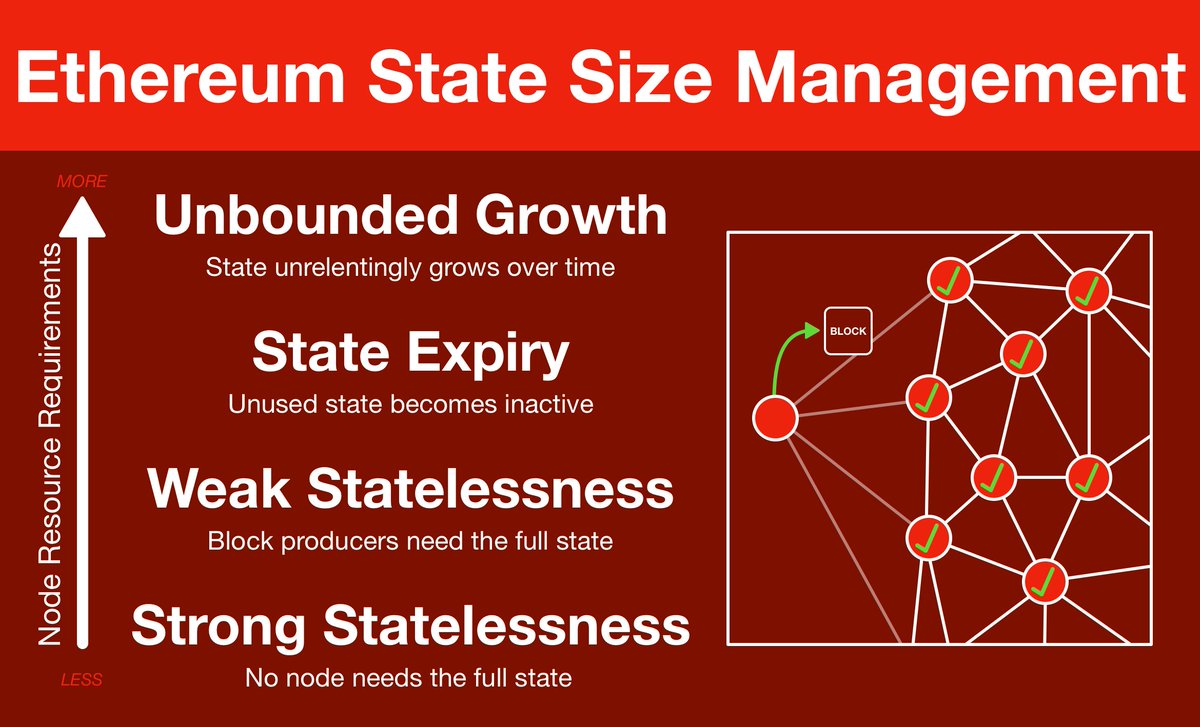
(8/25) What happens if we have a dataset too big for a Merkle tree?

IRL Example: the internal state of @ethereum is stored in a Merkle tree. This tree grows as more accounts & smart contracts are created. Eventually proofs are going to grow too big to push through the network.

(9/25) Let's start by asking the question "what's the purpose of a Merkle tree?"

A Merkle root is a unique string that is generated from a large dataset. With the root, anyone can verify the original dataset and/or an individual piece of data.

We call this a commitment scheme.

https://twitter.com/SalomonCrypto/status/1586809382813065216

(10/25) Our new scheme must avoid the bottlenecks that Merkle trees face; proof size must stay constant regardless of dataset size.

A Merkle proof contains the intermediate hashes needed to rebuild the root. What if we use cryptography to condense all of that into one value?

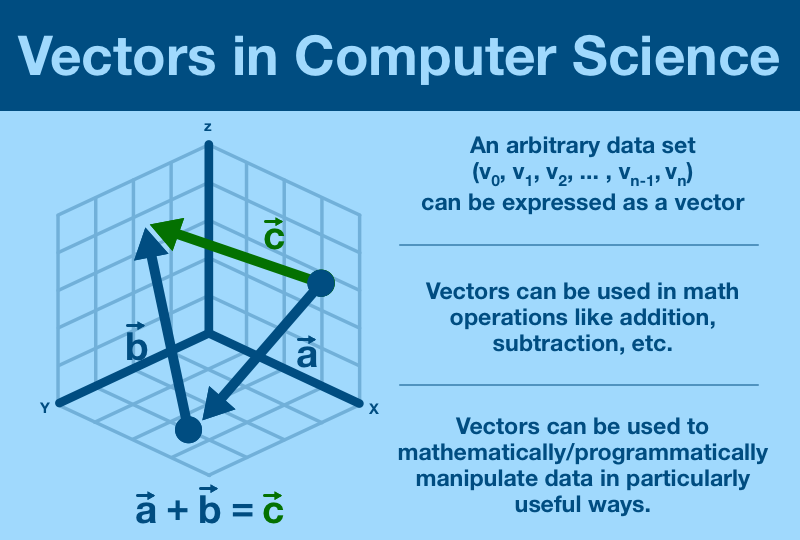
(11/25) We'll start with a Vector.

Tl;dr vectors are a concept used to convey quantities that cannot be expressed by a single number.

In two dimensions, "2 spaces right, 3 spaces up" can be represented as the vector (2,3)

A n-dimensional vector can express n data points.

https://twitter.com/SalomonCrypto/status/1586538963975565312

(12/25) Let's simplify how we think of Merkle proofs. The point of sharing all the intermediate branches is to generate the unique path from the Merkle root to your data point.

Let's think about expressing this value as a vector.

(13/25) This will form the foundation of Verkle tree. Here's more than you want to know on the name.

V = vector
erkle Tree = Merkle Tree

We will also be interested in Verkle tries which are trees organized by their keys (in example above, you can trace keys through inner nodes)

(14/25) Again, we've already built a scheme around a vector. The challenge is to build it so that the vector can be (trustlessly) transmitted with a constant size.

Fortunately, modern cryptography has developed lots of tools to solve this exact problem.

(15/25) For example, we could deploy KZG commitments for this purpose.

Tl;dr the KZG commitment scheme uses elliptic curve cryptography to commit to a polynomial.

A polynomial commitment is actually much more powerful than a vector commitment, but can also be used as one.

https://twitter.com/SalomonCrypto/status/1583705993300492288

(16/25) KZG commitments require too much computation for the Verkle trees we are interested in. We will use Pedersen commitments to commit to a vector.

I haven't gotten to that thread, but it's worth reading ahead. We will see Pedersen commitments soon.

(17/25) We will pick the particular scheme based on the application, but the point is that we directly prove the vector. Unlike Merkle trees, we do not need to first rebuild the vector before we prove it.

Individual vector components are of constant size.

(18/25) Remember, Merkle proofs grew in size as the underlying dataset grew (albeit more slowly). When we tried to decrease the number of vertical levels, we got even more horizontal components.

https://twitter.com/SalomonCrypto/status/1586391148993519617

(19/25) Verkle trees do not have this problem. Shortening the tree decreases proof size.

Here's a rough idea, but don't dwell too long on it. In fact, the cryptographic schemes we are looking are so powerful that we can simplify even further.

(20/25) KZG commitments, Pedersen commitments and all the other schemes we are considering can condense an arbitrary number of proofs into a single value.

Put another way, we can use the magic of elliptic curve cryptographic to create a single vector that serves for all proofs.

(21/25) @dankrad lays out the technique here in his blog. It's pretty in depth and technical, not for the feint of heart.

dankradfeist.de/ethereum/2021/…

(22/25) Which brings us to actual Verkle trees.

Verkle proofs don't scale with tree width and therefore can be incredibly wide. The current proposal for the @ethereum state is looking at a width of 256, but some are pushing for 1024.

(23/25) One might ask "can we make it infinitely wide?" We can, we can create a "Verkle tree" that is just a single level, making proofs incredibly lightweight.

In practice, this will cause a huge burden during the commitment generation phase.

(24/25) Turns out this might be an inherent property of commitment schemes, maybe like "in order to create a lightweight proof, a commitment needs to touch every piece of data."

If so, the commitment scheme design ends up becoming a trade-off between prover and verifier work.

(25/25) Verkle trees are an advanced improvement on an already complicated topic. But here's all you need to know:

- Verkle trees, like Merkle trees, allow verification of data within a dataset
- Verkle proofs are of constant size, regardless of dataset

More of a long-form reader? Try this out:

typefully.com/SalomonCrypto/…

Like what you read? Help me spread the word by retweeting the thread (linked below).

Follow me for more explainers and as much alpha as I can possibly serve.

https://twitter.com/SalomonCrypto/status/1587668139466113024