
After years of work, we are very happy to see our manuscript out that shows how fault-tolerant logical operations in #quantumcomputing based on #topologically-ordered phases of matter can be usefully interpreted as instances of #anyoncondensation.
scirate.com/arxiv/2212.000…
scirate.com/arxiv/2212.000…

We present a constructive theory for anyon condensation and, in tandem, illustrate our theory explicitly with examples of fault-tolerant logical operations for the #colorcode model. 

We show that different condensation processes are associated with a general class of #domainwalls, which can exist in both space- and time-like directions. This class includes semi-transparent domain walls that condense certain bosonic subsets of anyons. 

We use our theory to classify #topological objects and design novel fault-tolerant #logicgates for the color code. 
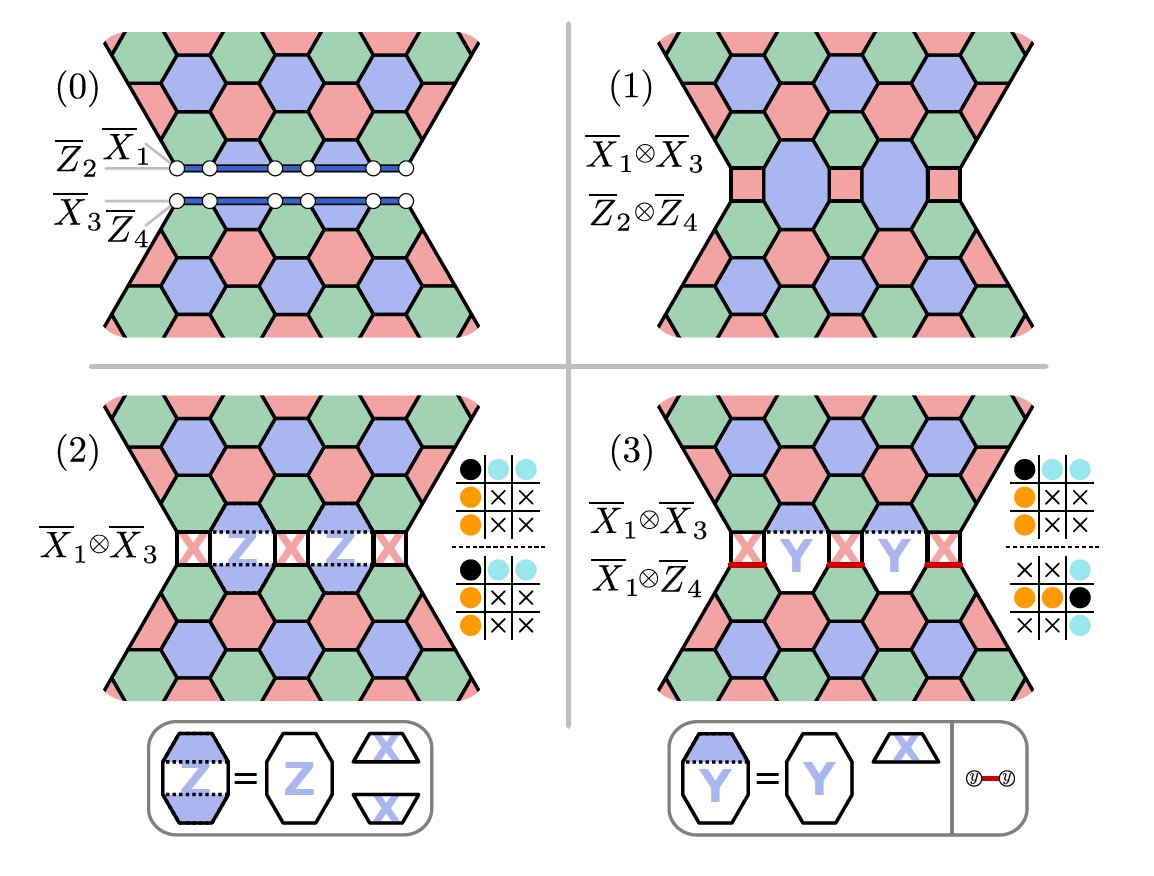
As a final example, we also argue that dynamical #Floquetcodes can be viewed as a series of condensation operations. 

We propose a general construction for realising planar dynamically driven codes based on condensation operations on the color code. We use our construction to introduce a new Calderbank-Shor Steane-type Floquet code that we call the #Floquetcolorcode. 

Warm thanks to Julio C. Magdalena de la Fuente, @felix_thomsen, @BartlettQuantum, @BenJamesBrown, and in particular @msKesselring for this wonderful and fun collaboration.
And thanks to our funders, in particular @BMBF_Bund (@QuantenTech #RealistiQ #QSolid), the @Einstein_Berlin (@ERU_Quantum) and @dfg_public (#CRC183) for generous support.
On a higher level, it is yet another example how fruitful the study of the interface between #quantuminformation theory and #condensedmatter physics can be.
(@QSolid_DE, that is.)
After my departmental colloquium, the first author approached me with a compelling idea how the comprehensive picture of anyon condensation can be completed.
• • •
Missing some Tweet in this thread? You can try to
force a refresh




