Thread by @hagertynw

2 useful papers today on how you can get basically any answer you want from regressions using arcsinh(y) or log(y+1)

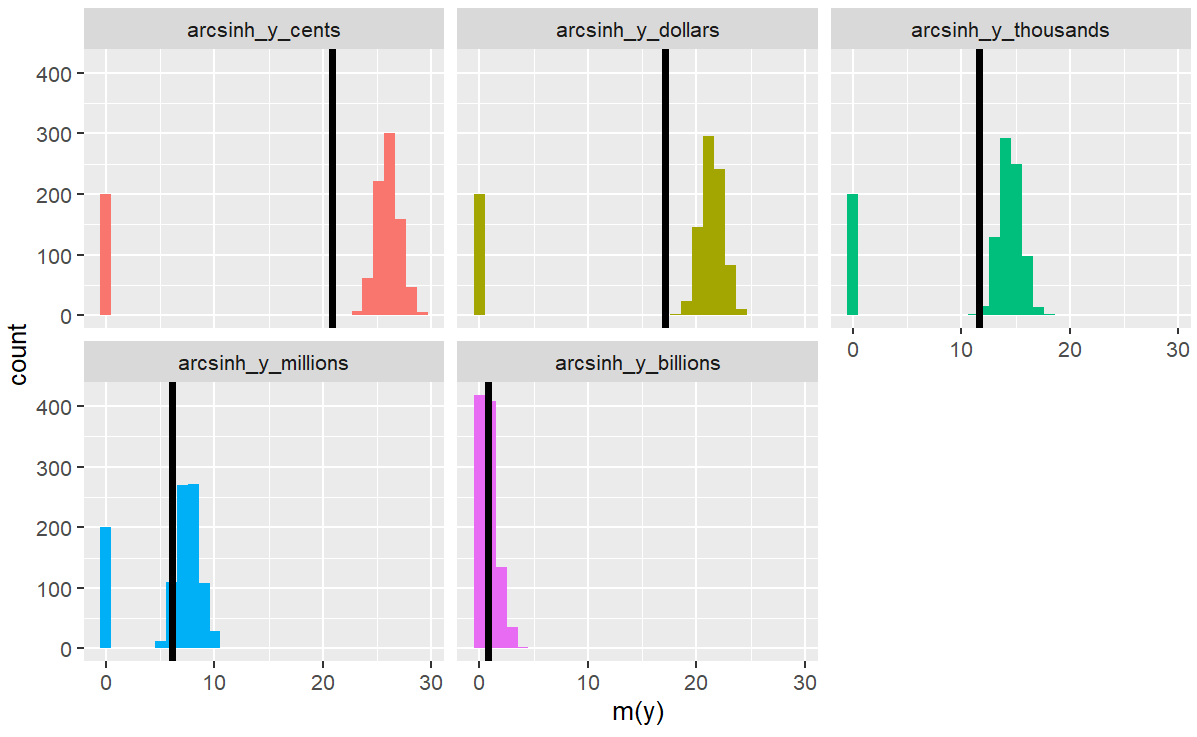
I made these graphs to show the problem: The mean of the transformed var (black lines) varies like crazy by what units you choose for y

🧵 on my own take-aways

Here are the papers:

One by @jondr44 and @jiafengkevinc

https://twitter.com/pedrohcgs/status/1602373738536005632?s=20&t=JZVqcs3pvhw0dUopFhs2cQ

The other by @JohnMullahy and @healtheconnort1

https://twitter.com/PHuenermund/status/1602216717396107265?s=20&t=OeU8Mrzbk_TfuNFfuyJ0Jw

Essentially: The 1 in log(y+1) is arbitrary (why not 10? 0.1? 0.0001?), and the arcsinh formula contains a similar hidden parameter

So they're sensitive to scaling, which isn't great because our answers should be the same whether we work with $, hundreds of $, millions, etc.

(I think economists could benefit generally from thinking more about units! In physics EVERYTHING is about unit analysis, which gave me helpful intuition)

(I've been trying to tell people about this problem for years, though I've used the arcsinh too so I'm totally a hypocrite)

Chen & Roth show that a "percentage" average treatment effect is *just not a well-defined estimand* when your outcome values can include 0.

I find this tremendously disappointing!! 😥 Though it seems obvious in retrospect, I think I'd been holding out hope for a way to get it

Also: Mullahy & Norton show that when you place the 0's far from the rest of the distribution (when units are small or c in log(y+c) is large), you're basically just estimating a linear probability model!

Intuition: you're putting more weight on the extensive margin

So what can we applied researchers do instead?

Here are the suggestions from both papers, along with my immediate reactions (which may or may not add value...)

1. (Mullahy & Norton) Forget the proportional treatment effects, just estimate OLS on the untransformed outcome.

I don't like this because
(a) I often care more about the avg proportional change than the avg level change across individuals
(b) estimates can be noisy for skewed y

2. (M&N) Use Poisson regression.

Poisson helps concern (b) but not (a). It directly estimates the log difference of the means in the treatment & control groups: log(E[Y(1)]) - log(E[Y(0)])

Not the average log difference: E[log(Y(1)) - log(Y(0))], which is what I tend to prefer

Poisson gets at moments of the conditional distributions. It's not guaranteed to tell you about the avg proportional change across individuals

Just like how quantile treatment effects tell you how the quantile ITSELF moves, not the treatment effect for indivs at a given quantile

In the framework of Chen & Roth, Poisson does not estimate a parameter of the form E[g(Y(1), Y(0)], at least not when you allow for arbitrarily heterogeneous treatment effects across individuals.

3. (Chen & Roth) Estimate the treatment effect for a
manually-calculated percentage change, like Y/Y_pre.

I like this idea, but:
- it requires panel data
- in my own experience it introduces a lot more noise
- it might not un-skew the variable if it isn't pretty autocorrelated

4. (C&R) Take a stand on how much you value the extensive margin. Estimate ATE for m(y) =
=log(y) for y>0 and
=-x for y=0,
where you choose x based on theory.

This is exactly what we're doing already, but without hiding the parameter choice!

5. (Both papers) Use a two-part model to separate the extensive and intensive margins.

This requires some further structural assumptions (though they can be weak if you're OK with bounds instead of a point estimate)

Think I need to review/learn more how to implement these!

Another note for any econometricians who might be listening... a "proof sketch" that involves supermodularity and Frechet-Hoeffding bounds is not exactly, uh, accessible to us applied researchers 😂

(I understand your incentives of course -- this is a structural complaint lol)

Somehow I missed @jiafengkevinc's own thread --

https://twitter.com/jiafengkevinc/status/1602403378809647104?s=20&t=EFda3xsP9NtStnGBZ-jbbg