Thread by @SrinivasR1729

SRINIVASA RAMANUJAN: An Enigmatic Genius
By K. Srinivasa Raghava.
This December 22 marks the 135th birth anniversary of our own great mathematician Srinivasa Ramanujan-FRS and is observed as National Mathematics Day (GANIT).
1/n

The man who brought India to the World Mathematics Map is regarded as one of the greatest thinkers of the modern world without any formal education in Mathematics. Dreamt and it’s there is not always possible for a normal person without ample effort.
2/n

But the story is different for Ramanujan, a self-taught mathematician, who in his 32 years of life span on this earth has gifted his dreams to the whole world and never shied from making the effort to any extent.
3/n

Ramanujan was one of the greatest mathematical geniuses ever to emerge from India. Srinivasa Iyengar Ramanujan, commonly known as Ramanujan was born at Erode in the Madras Presidency on 22nd December 1887 to a Sri Vaishnava Brahmin Family.
4/n

Ramanujan early showed a strong inclination toward mathematics. His extraordinary powers appear to have been recognized almost immediately. He was quiet and meditative and had an extraordinary memory.
5/n

He astonished his friends and teachers by mentally calculating, too many decimal places, the values of π, e, and other mathematical constants.
6/n

Ramanujan used to ask puzzling questions about "zeros and imaginary quantities," the "distances of stars” and the value of zero divided by zero and the like. By the age of 13, he completely mastered the book on advanced trigonometry written by S. L. Loney.
7/n

He found his own method of solving cubic equations at the age of 15. In elementary school, he won numerous awards for his calculating skills. Upon graduation in 1904, he won a scholarship for higher studies in Govt. College, Kumbakonam.
8/n

In 1903 when he was 16, Ramanujan borrowed a copy of a book by G. S. Carr, titled ‘A Synopsis of Elementary Results in Pure and Applied Mathematics, it was this book that awakened his genius.
9/n

He set himself to establish the formulae given therein. Consumed by his passion for mathematics, Ramanujan neglected all other subjects. As a result, he failed the entrance exam for the University of Madras.
10/n

However, he continued his mathematical research with intensity and, by his early twenties, had become known to the leading mathematicians in the region. On 14 July 1909, Ramanujan was married to a nine-year-old bride, Janaki Ammal,
11/n

after marriage, he searched for a job, and for the next three years he held no serious job; he went door to door around the city of Madras looking for a clerical position. Despite his poverty, Ramanujan continued to immerse himself in mathematics.
12/n

He scribbled his formulas, expressed in irregular and non–standard notation, in a series of scruffy notebooks. Ramanujan was an ardent follower of the Hindu goddess Namagiri Devi. After receiving visions from the goddess in the form of blood droplets,
13/n

Ramanujan saw scrolls that contained very complicated mathematics like Elliptic integrals, Hyper-geometric series, etc. It was a remarkable fact that frequently, on rising from bed, he would note down results and rapidly verify them,
14/n

though he was not always able to supply rigorous proof. Ramanujan managed to secure a clerical job at the Madras Port Trust office in the accounts department.
15/n

Ramanujan published his first research paper titled ‘Some properties of Bernoulli
Numbers’ in the Journal of the Indian Mathematical Society in the December issue of Volume 3 in 1911. Along with the paper, Ramanujan proposed some intricate questions.
16/n

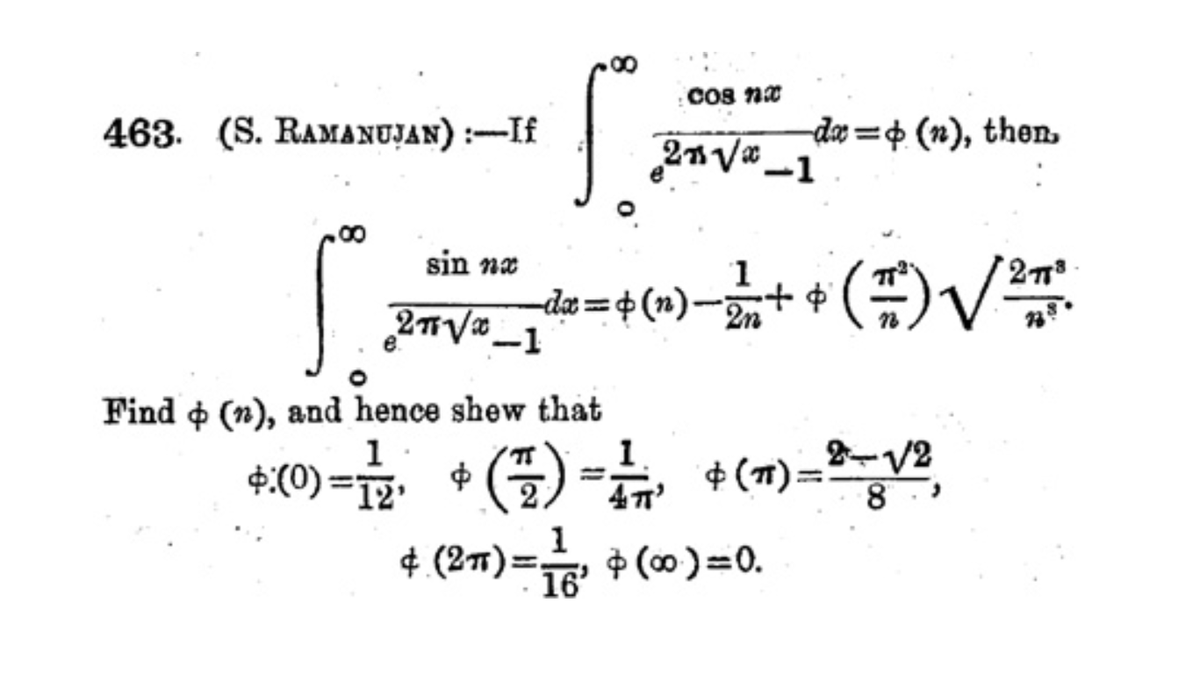
Since there were at that time no mathematicians in India capable of understanding his extraordinary talent, Ramanujan, In January 1913 he wrote a 10-page letter containing 120 theorems to another renowned British mathematician Prof. G. H. Hardy of Trinity College,
17/n

Cambridge is also the Fellow of the Royal Society. He was amazed and intrigued by the theorems that Ramanujan had included in the letter. Hardy, himself a man of extraordinary ability, reviewed Ramanujan’s strange-looking theorems and concluded,
18/n

“A single look at them is enough to show that they could only be written down by a mathematician of the highest class. They must be true because, if they were not true, no one would have had the imagination to invent them.”
19/n

Hardy took a keen interest in Ramanujan’s work and decided to bring Ramanujan to Cambridge to pursue some serious research. Furthermore, a special research scholarship of Rs.75/- per mensem was awarded to him for two years by the University of Madras.
20/n

Ramanujan thus became a professional mathematician and remained so for the rest of his life. Ramanujan was very pleased to receive an invitation from Hardy to work with him at Cambridge but his journey to England was delayed by a religious prohibition against foreign travel.
21/n

During that time Ramanujan's mother had a vivid dream in which the family Goddess Namagiri commanded her "to stand no longer between her son and the fulfillment of his life's purpose" also Ramanujan had a vision from the Goddess granting him permission to go to Cambridge.
22/n

Thus, on 17th March 1914, Ramanujan sailed to England. At Cambridge Ramanujan started working with Hardy and Littlewood, He was now for the first time in his life in a really comfortable position and could devote himself entirely to his mathematical research.
23/n

Ramanujan and Hardy shared their unique mathematical perspectives, and they arrived at some startling discoveries, especially in Analytic number theory and Modular forms.
24/n

They found an astonishing formula to count the number of partitions of an integer (Partition function) now that has important applications in modern physics.
25/n

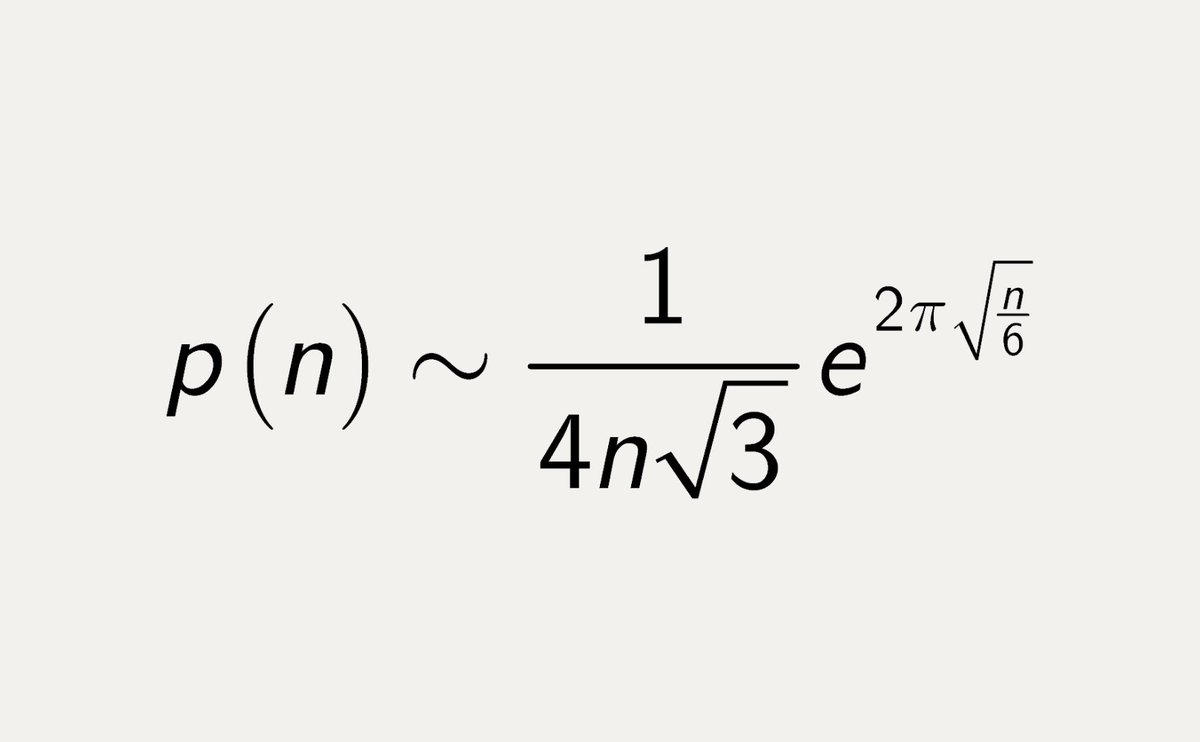
Ramanujan returned to India in fragile health, He was believed to be tubercular, but is now thought to have suffered a severe vitamin deficiency (Amebiasis). His sickness was not curable and he died at the age of 32 on 26th April 1920.
26/n

However, Ramanujan spent his last year producing some of his most profound theorems including Mock Theta functions, q-series, Diophantine equations, Reciprocal functions, Mordell integrals, Continued fractions, and Modular forms.
#Ramanujan #mathematicsday #Mathematics
27/n

Ramanujan’s life was tragically short. However, his mathematical discoveries are still alive and flourishing. The work of Ramanujan was so unparalleled, unprecedented & rich that just the side comments on his work are enough to keep seasoned mathematicians busy even now.

28/n

A century later, the legacy of this genius continues to influence mathematics, physics, and computation fields. He was an intellectual who was ahead of his time and a groundbreaking pioneer in the field of mathematics
29/n

which is why today is rightly celebrated as National Mathematics Day as well!
Surprisingly in 2012 scientists found a profound and precise relationship between
30/n

Ramanujan’s cryptic mock theta functions and the hottest item in theoretical physics - string theory and black holes.
Great people live short lives, sometimes. May the young be inspired by such beautiful minds!
#Ramanujan #mathematicsday
31/n