Thread by @__ivan_init__

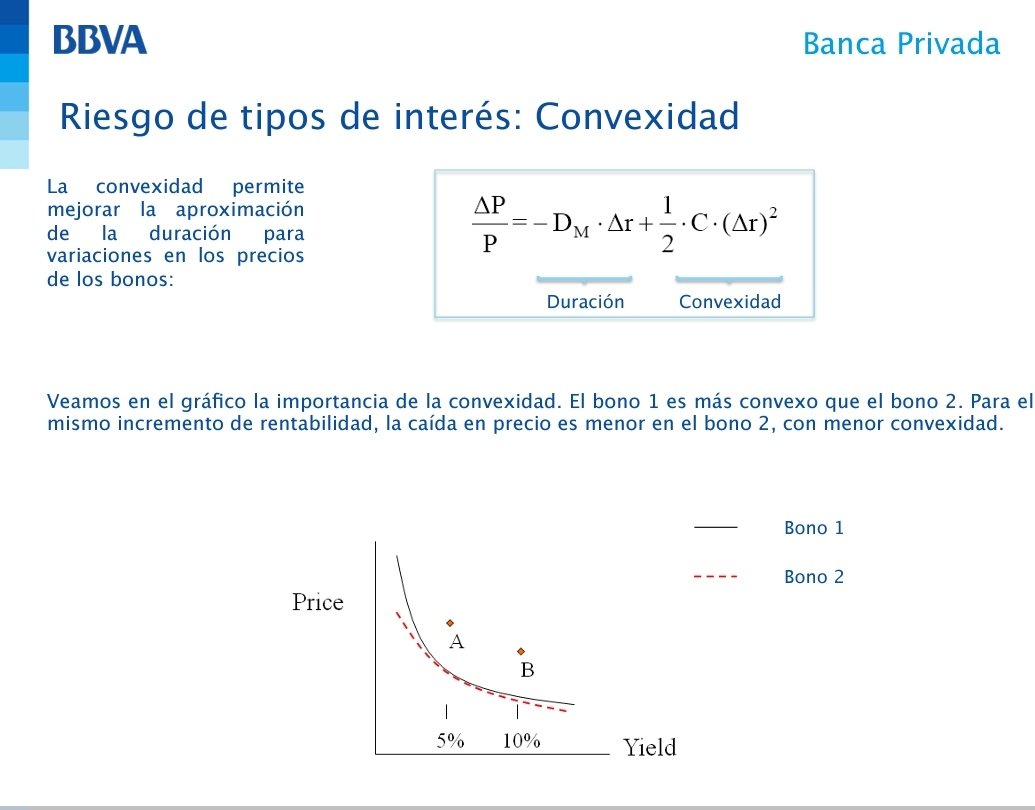
El otro día hablé de Taylor para aproximar variaciones en el precio de un bono. Sin embargo, hay algo mucho más interesante: las variaciones en el precio de una opción.

Las opciones son derivados NO lineales. Eso nos da un juego brutal. Ese juego son las griegas.

Recuerdo mi primera entrevista de trabajo. Me preguntaron por opciones. Yo las había dado en la carrera. Ciertas cosillas muy introductorias. En ese momento me preguntaron por las griegas. Dije: ¿eso qué es? En verdad, las griegas son la clave de las opciones. Sin saber

manejarlas bien, no sabes opciones. Lisa y llanamente. Los grafiquitos de payoff de una call y una put están bien, pero no te sirven ni para empezar. Porque al final el problema que se esconde en el mundo de las opciones es que la no linealidad nos fuerza a hacer análisis de

sensibilidades mucho más complejos. El trading de opciones es el trading más complejo que hay con mucha diferencia. Yo reconozco que es la parte que más me gusta de las finanzas. Con diferencia. Dedicaré algunos hilos a opciones, pero por atacar el asunto sucintamente: ¿qué

son las griegas? El problema de la aproximación de las variaciones en el precio de un bono es un problema relativamente sencillo. Estamos aproximando una función de una variable (la TIR del bono). Es un polinomio de Taylor al uso, en una variable.

Con las opciones la cosa se complica. El precio de una opción depende de muchos parámetros (el precio del activo subyacente, el tipo de interés, la volatilidad, el tiempo a expiry...), por lo que tenemos que meternos en análisis de sensibilidad con derivadas parciales. Es decir,

un polinomio de Taylor en varias variables. En un polinomio de Taylor en varias variables aparecen primero las parciales de primer orden, después las parciales de segundo orden y las cruzadas. Y así hasta que queramos cortar. Pues en opciones cortamos en las de segundo orden.

Y cada derivada parcial tiene nombre. Ese nombre es el nombre de una letra griega. Las griegas son las parciales de la opción (valorada en un marco Black) respecto a sus distintos parámetros. Las más importantes: delta, gamma, vega, rho, vanna y volga. Y son unas capullas.

Cada una va por su lado. Si queremos cubrir el riesgo en una cartera con opciones tendremos que cubrir todas las griegas relevantes. Al mismo tiempo. Con las opciones no basta cubrir una vez y me olvido (hedging estático). Hay que cubrir muchas y repetidas veces (hedging

dinámico). Y muchas coberturas tratan de parchear tramos no lineales con linealidades, como es el caso de la cobertura en delta, la más importante que hay. La idea es un poco esta del dibujo (sí, no soy Picasso, lo sé).

Aquí tenéis otro mundo al que os podéis dedicar los que os gustan las finanzas. Tenéis desde las opciones más vanilla (más estándar) hasta las más exóticas. Y en este mundo hay que ir bien fuerte en mates.