Thread by @__ivan_init__

Este joven se llamaba André-Louis Cholesky. Desde las trincheras dejó para la posteridad uno de los resultados más importantes de Álgebra Matricial de la historia. Al menos para los financieros.

Murió poco antes de acabar la guerra. Sirva este hilo como un pequeño homenaje.

Prácticamente toda la probabilidad y la estadística están construidas sobre la noción de independencia. No por nada, simplemente por simplicidad. Suponer que los fenómenos aleatorios son independientes entre sí nos hace la vida mucho más fácil. Pero llega un punto en que esto

es imposible. Por poner un ejemplo: las acciones de distintas compañías guardan relación entre ellas, exhiben un comportamiento conjunto, están correladas. Cuando las acciones de un banco español se desploman, a no ser que sea algo muy idiosincrásico, las acciones del banco de

al lado se desplomarán también. Necesitamos captar esto en nuestros modelos. Y la forma de hacerlo pasa por la famosa descomposición de Cholesky, una de las factorizaciones matriciales más usadas a día de hoy. Primero, ¿en qué consiste una factorización matricial? Pues

básicamente en expresar una matriz como producto de matrices más simples. Esto nos permite resolver sistemas mucho más fácilmente, por ejemplo, además de simplificar la puesta en marcha de muchos algoritmos que involucran operaciones con matrices. La descomposición de Cholesky

es una de esas factorizaciones. De hecho, lo que haremos será aplicarle a la matriz de correlaciones entre los distintos activos la factorización de Cholesky. Una vez aplicada, nos quedaremos con una de esas matrices "más simples" que han salido de la descomposición. Esa matriz

más simple está preparada para imprimir en el vector aleatorio la estructura de correlaciones deseada. Grosso modo, así es como operamos. La descomposición de Cholesky básicamente coge una matriz hermítica y definida positiva (ahora diré lo que es eso) y la factoriza en el

producto de una matriz triangular inferior (todo ceros encima de la diagonal) y otra matriz triangular superior (todo ceros debajo de la diagonal). Sin embargo, no todas las matrices admiten una descomposición así. Y esto a priori es un problema gordo. No obstante, la matriz de

correlaciones sí la admite. ¿Por qué? Primero, porque son matrices hermíticas. ¿Qué es una matriz hermítica? Una matriz que coincide con su conjugada traspuesta. En R, un número y su conjugado coinciden, por lo que simplemente matrices que coinciden con su traspuesta. Vaya,

una matriz simétrica. Es decir, en el caso de trabajar con números reales, esa condición se convierte en que sea una matriz simétrica. ¿Y qué significa lo de definida positiva? Básicamente que todos sus autovalores sean positivos. Y ojo, porque al ser una matriz simétrica,

la matriz será "semejante" a una matriz diagonal. Existe una matriz de paso (un cambio de base) que me la diagonaliza. Pongo lo de semejante entre comillas porque en rigor en este caso habría que poner congruente. En el caso de las matrices simétricas, nos aseguramos la

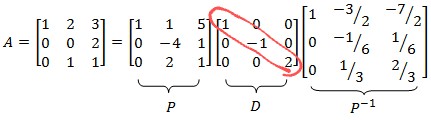
diagonalización por medio de matrices de paso ortogonales. Y esto cambia un poco la naturaleza de la diagonalización, básicamente por lo siguiente. La diagonalización estándar sería algo así. El tema es que una matriz ortogonal es aquella cuya inversa coincide con su traspuesta.

Eso implica que la inversa que veis ahí, P^(-1), se transforma en la traspuesta, Pt. En definitiva, los autovalores son los números que aparecen en la diagonal de la matriz D. Como veis, esa matriz no es definida positiva. Lo sería si todos esos valores fueran mayores que cero.

Una problemática que solemos encontrarnos en finanzas es cuando la regulación nos suministra ciertas correlaciones normativas. Vamos, correlaciones que se inventa el regulador para aumentar los recargos de capital. Y entonces la matriz no tiene por qué ser una matriz de

correlaciones. Puede que le falle la condición de que sea definida positiva, y ahí tenemos que introducir técnicas de recuperación (o salvamento) de la estructura de la matriz de correlaciones. Si no, nos quedamos sin Cholesky. Para que veáis la ingente cantidad de herramientas

que tenemos. Es una locura. Al final tienes que manejar con soltura todas las ramas de las matemáticas. El trabajo de quant la verdad es que tiene su miga.