Thread by @Tim_Dettmers

We present SpQR, which allows lossless LLM inference at 4.75 bits with a 15% speedup. You can run a 33B LLM on a single 24GB GPU fully lossless. SpQR works by isolating sensitive weights with higher precision and roughly doubles improvements from GPTQ: arxiv.org/abs/2306.03078🧵

Rapid-fire results 1/2:
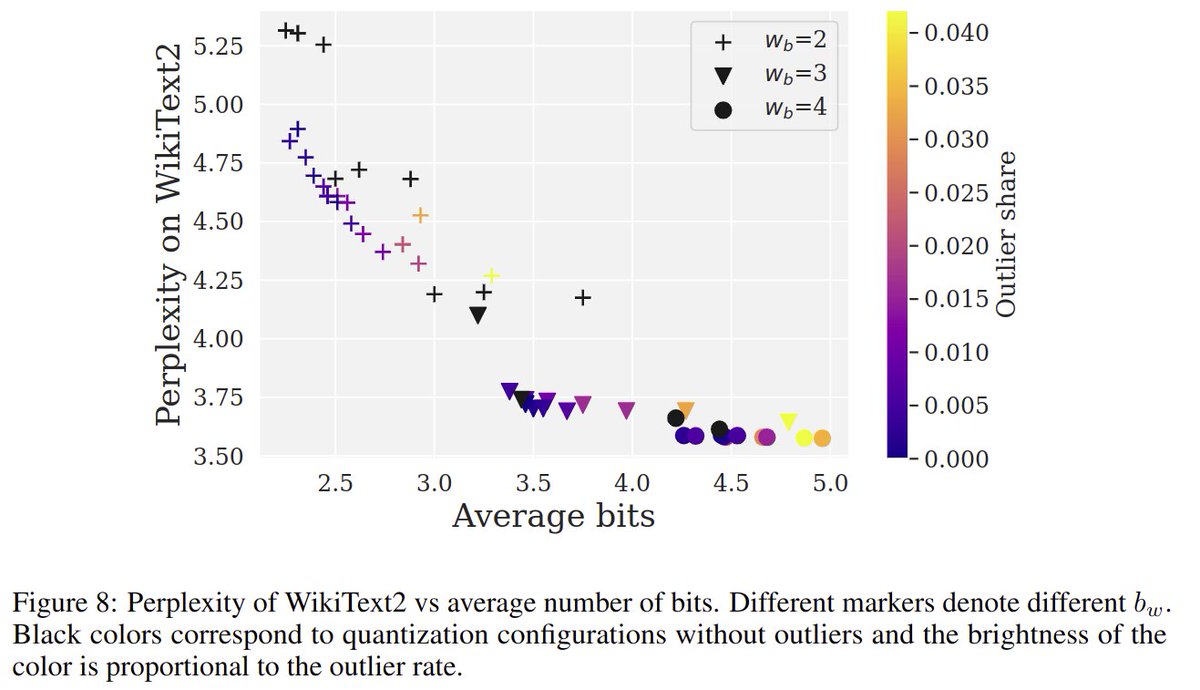
- 4.75 bit/param lossless; 3.35 bit/param best performance trade-off
- Performance cliff at 3.35 bits that is difficult to overcome
- 13B/33B LLaMA fits into iPhone 14/colab T4 with 3.35 bits
- 15% faster than FP16; ~2x speedup vs PyTorch sparse matmul

Rapid-fire results 2/2:
- row outliers seem to be responsible for creating column outliers in the next layer
- larger outliers in later layers
- probably due to the GPTQ procedure, outliers get larger in the last matrix dimensions

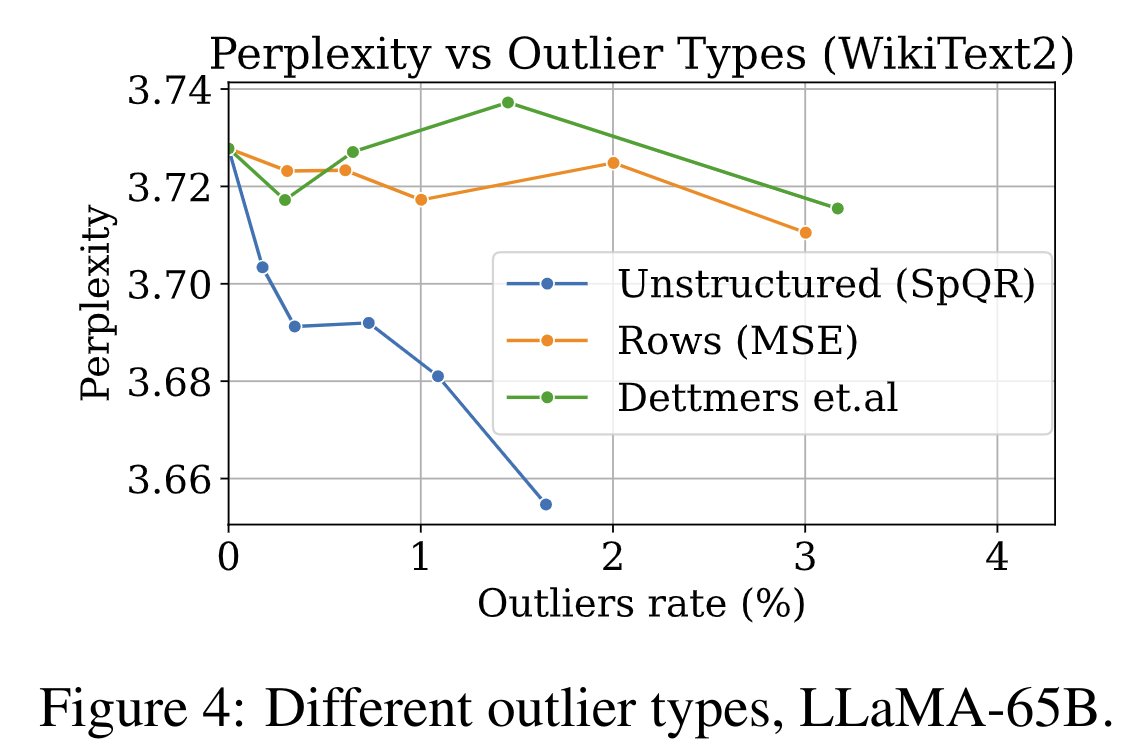
SpQR is the result of a careful analysis of how sensitive outliers weights in the GPTQ algorithm affect outcomes. Besides column outliers found in LLM.int8(), we also find partial row outliers (that sometimes skip attention heads) and unstructured outliers.

When we try to exploit these structures, we find that the best way to reduce the error with as little memory as possible is to not enforce any structure. This means that the chaos of partial row, column, and unstructured outliers can be best tamed with a fully sparse algorithm

Sparse algorithms can be super tricky to implement. So for SpQR we had to develop both, a new sparse matrix multiplication algorithm and the storage format. The end result is a little complicated ... 😅But we still managed to get a small memory footprint (3.3 bits) and speedups.

The last innovation is bilevel quantization. It was developed in parallel to double quantization by my colleagues and is a strict improvement. We quantize the 1st order quantization by a 2nd order quantization that both has zero points and scales that are in 3-bit.

Putting unstructured outliers together with bilevel quantization and the GPTQ procedure (minimizing quantization errors by counter-balancing rounding decisions to reduce error).

In SpQR we combine quantized and sparse matmul. To speed up sparse matmul over regular cuSPARSE/PyTorch matmul we exploit the fact that we have some partial structure. Instead of loading the "correct" elements. We load more values and filter out the right ones in fast SRAM cache

While the accuracy and perplexity numbers tell a story of "no degradation," this is difficult to grasp how this translates into generation quality. Here are some examples that I found very instructive:

8-bits, 4-bit, 3.35-bits, how much time to hit 1-bit? We see a hard cliff with SpQR at around 3.35 bits, and it isn't easy to get further with this algorithm. But there are already follow-up ideas. I think we will get to 3-bit within 2-3 months. 2-bit is hard to crack, though.

SpQR is the product of an ensemble cast of talented researchers — it felt like I was just along for the ride! Thank you to my co-first authors Ruslan Svirschevski, Vage Egiazarian, Denis Kuznedelev, and @elias_frantar, @AshkboosSaleh, @sasha_borzunov, @thoefler, @DAlistarh!