Thread by @carlislerainey

Do you use logistic regression? If so, you’ll want to read the thread below.

⚠️ Warning: Memes, charts, #rstats, and practical advice ahead.

If you don’t like Twitter shenanigans, I’ll give it away.

For logit models with small-to-moderate samples (maybe N < 1,000), you should consider Firth’s penalized estimator.

I talk about it in this paper with Kelly McCaskey (open access!).

cambridge.org/core/journals/…

Now on with the thread!

Logit models are really common in the social sciences. We typically use maximum likelihood (ML) to estimate these models. But the excellent properties of these models are mostly asymptotic.

However, these estimates might not be well-behaved in small samples. In particular, some folks are concerned about small sample bias in logit models. And that’s a real thing.

(But I don’t think it’s the most important problem—keep reading.)

The figure below shows the percent bias in the coefficient estimates for different constants and numbers of explanatory variables (k) as the sample size varies. It’s hardly negligible, but it disappears quickly.

Fortunately, David Firth came along and suggested a *penalized* maximum likelihood estimator that eliminates almost all of this bias.

jstor.org/stable/2336755

If this seems familiar, it should. Zorn’s (@prisonrodeo) (2005) paper is a classic in political science methods classes, and he recommends Firth’s penalty to deal with separation.

cambridge.org/core/journals/…

Here’s what Firth’s penalty looks like. You just maximize the penalized likelihood L* rather than the usual likelihood L.

And it really works! Here’s a comparison of the percent bias in the ML and PML estimators. You’ll see that Firth’s penalty just wipes most of the bias away.

BUT WAIT!!!! 🛑

If you’re clever, you’ll ask about variance. Most of the time, when you reduce bias, you increase variance. You have to choose!

But that’s not what happens here.

When you use Firth’s logit, you shrink *both* bias and variance.

That means you don’t have to choose between bias and variance. You can reduce BOTH.

Here’s a figure showing how much more variable your estimates will be if you use ML rather than Firth’s PML.

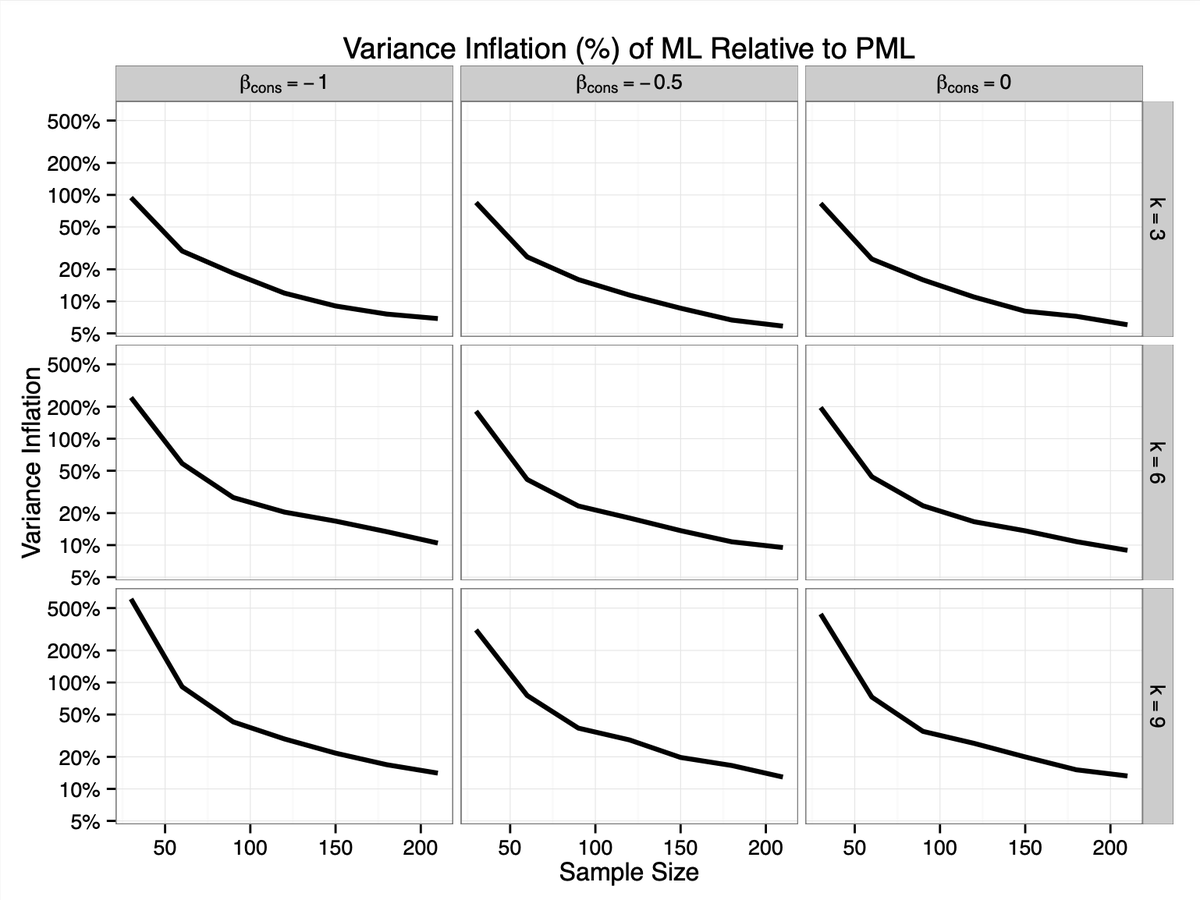
But even more importantly, it turns out that bias isn’t the big problem in the first place. The shrinkage in the variance is much more important than the reduction in bias.

In many common scenarios, the variance might contribute about 25 times more to the MSE than the bias (or higher).

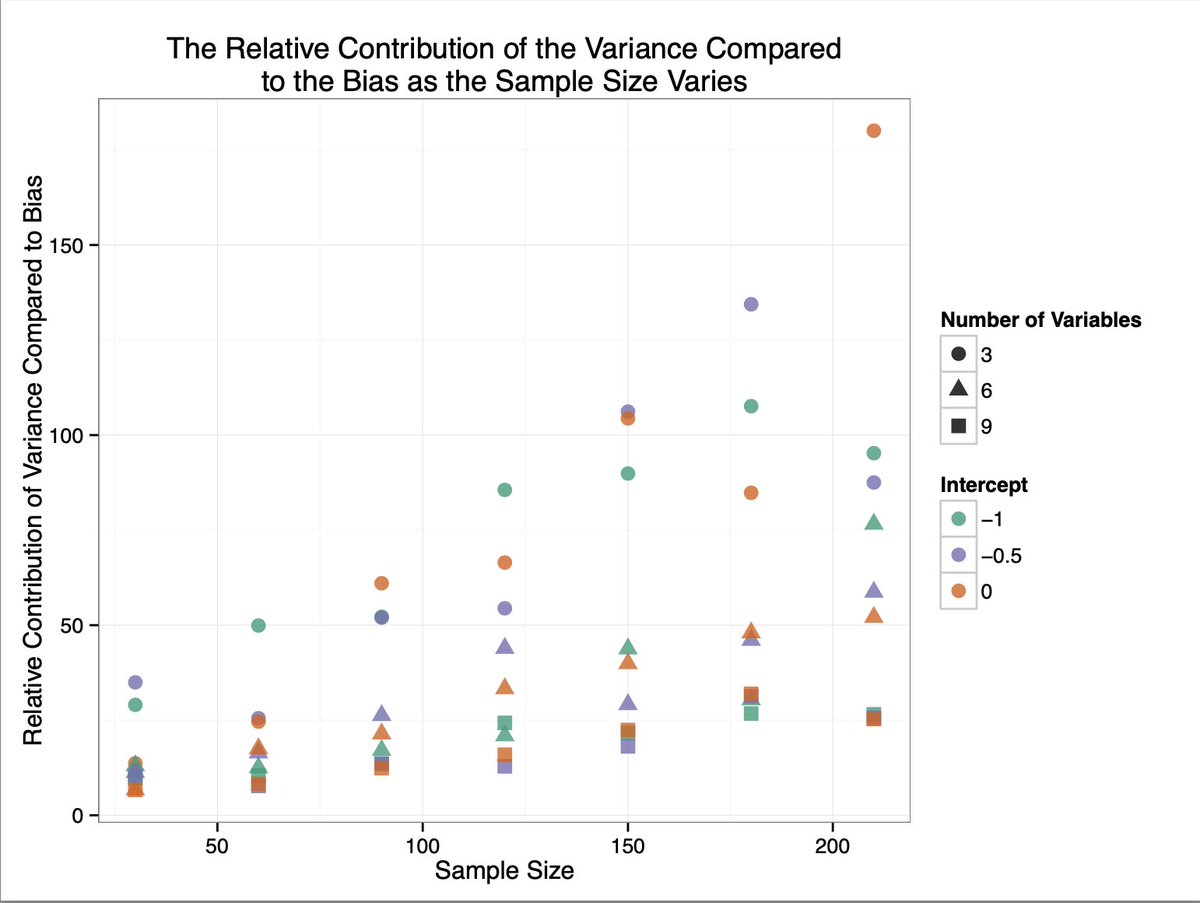
So you shouldn’t really be using PML to reduce bias; you should be using PML to reduce *variance* (and bias).

All of this means that you should usually use *penalized* maximum likelihood to fit logistic regression models.

As a default, Firth’s penalty makes much more sense than the usual maximum likelihood estimator.

In practice, that means using the {brglm2} package rather than glm().

And Twitter will love this! {brglm2} works with @VincentAB’s {marginaleffects} package and @noah_greifer’s {clarify} package.

And it can make a big difference! Here’s a comparison for a small data set from Weisiger (2014).

Paper here:

Code here: journals.sagepub.com/doi/pdf/10.117…
gist.github.com/carlislerainey…

Here's the plot

In short, I think Firth’s PML is usually preferable to ML for fitting logit models. It’s always better in theory (smaller bias and variance), easy to implement (brglm2), makes BIG difference in small samples, and a meaningful difference in much larger samples (e.g., N = 1,000).

If you’re interested in this topic, then I recommend the work of Ioannis Kosmidis (@IKosmidis_).



ikosmidis.com
twitter.com/IKosmidis_

And here’s a nugget for #econtwitter. For a simple treatment/control design with a binary outcome, Firth’s logit produces a better estimate of the ATE than OLS.

I’ve got lots more thoughts on this that I might put in a blog post, but for now, here are two takeaways.

<1> This “small sample” problem is a problem for even larger samples (perhaps larger than 1,000).

<2> The real problem isn’t bias; the problem is variance.

If you’re interested, here’s the paper (with Kelly McCaskey) that describes all the details. It’s open access.

cambridge.org/core/journals/…

And a little tidbit that popped up elsewhere.

Super interesting.

https://twitter.com/sp_monte_carlo/status/1686512695107874818

Nice links here!

https://twitter.com/IKosmidis_/status/1686687290129580032

And here’s a really clever application of Firth’s method to panel data in political science from @CookScottJ.

Ungated:

Journal (@PSRMJournal): sites.pitt.edu/~jch61//PS2740…
cambridge.org/core/journals/…

On Firth and GLMM:

https://twitter.com/IKosmidis_/status/1696866496071234026