Thread by @GregBodwin

This is a thread about a recent cursèd result in graph theory that I enjoy.

It's about graph coloring. For background, a coloring of a graph is an assignment of colors to the nodes, so that every edge is multicolored.

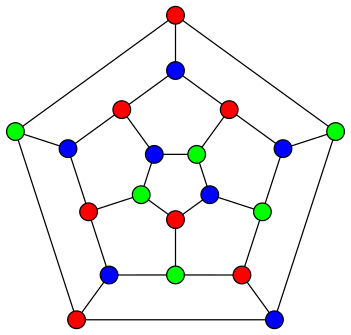
A neat fact ("Brooks' Theorem") says that every r-regular connected graph can be colored using r colors, with the only exceptions being cliques and odd cycles. We will talk about such graphs. For example, all nodes above graph have deg 3, and we colored it using only 3 colors.

We might ask if this coloring is *unique.* But the answer is obviously no: certain trivial operations change one valid coloring into another. For example, we could recolor all blue nodes green and all green nodes blue.

A bit more generally, we can swap two colors in just one part of the graph: choose two colors, find an island of nodes containing only these two colors, and exchange the colors only on that island.

So now we might ask again if there is always a unique coloring, up to this basic operation. Can we always get from one valid coloring to another by applying this recoloring trick a few times?

Sadly, the answer is still no. The counterexample is the triangular prism graph. We can't get between the following two valid colorings using this recoloring trick. (figure from ) arxiv.org/pdf/1510.06964…

And now the punchline: that's the only counterexample. Every other r-regular graph has a unique coloring, up to the recoloring trick. I have no intuition at all for what makes the triangular prism graph special.

Cites: the recoloring trick is called a "Kempe Change," and this theorem was proved by Bonamy, Bousquet, Feghali, and Johnson (). Previously the special case r=3 was proved by Feghali, Johnson, and Paulusma ()arxiv.org/abs/1510.06964
arxiv.org/abs/1503.03430