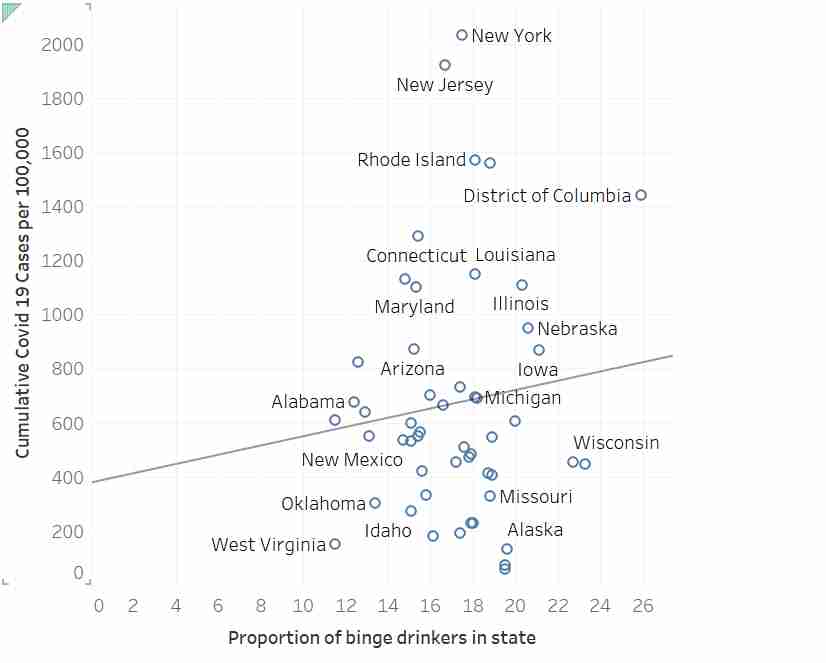
Forgive me, for I am about to Bayes. Lesson: Don't trust intuition, for even simple prior+likelihood scenarios defy it. Four examples below, each producing radically different posteriors. Can you guess what each does? Revealed in next tweet >> 

Huzzah! Posterior distributions in red. The shape of the tails, which isn't so obvious to the eye, can do weird but logical things. 

Gotta go to a meeting, but I will return to explain each of the four above later!
These are combinations of normal (Gaussian) & student-t (df=2) distributions. Gaussian has a very thin tails. Student-t has thicker tails.
Top-left: normal prior, normal likelihood
Top-right: student, student
Bottom-left: student, normal
Bottom-right: normal, student
>>
Top-left: normal prior, normal likelihood
Top-right: student, student
Bottom-left: student, normal
Bottom-right: normal, student
>>
Normal prior, normal likelihood
y ~ Normal(mu,1)
mu ~ Normal(10,1)
The classic flavor of Bayesian updating - the posterior is a compromise between the prior and likelihood
y ~ Normal(mu,1)
mu ~ Normal(10,1)
The classic flavor of Bayesian updating - the posterior is a compromise between the prior and likelihood

Student prior, student likelihood (df=2)
y ~ Student(2,mu,1)
mu ~ Student(2,10,1)
The two modes persist - the extra mass in the tails means each distribution finds the other's mode more plausible and so the average isn't the best "compromise"
y ~ Student(2,mu,1)
mu ~ Student(2,10,1)
The two modes persist - the extra mass in the tails means each distribution finds the other's mode more plausible and so the average isn't the best "compromise"

Student prior, normal likelihood
y ~ Normal(mu,1)
mu ~ Student(2,10,1)
Now the likelihood dominates - it's thin tails are very skeptical of the prior, but the prior's thick tails not so surprised by the likelihood
y ~ Normal(mu,1)
mu ~ Student(2,10,1)
Now the likelihood dominates - it's thin tails are very skeptical of the prior, but the prior's thick tails not so surprised by the likelihood

Normal prior, student likelihood
y ~ Student(2,mu,1)
mu ~ Normal(10,1)
Now the prior dominates, so reason as previous example but in reverse
y ~ Student(2,mu,1)
mu ~ Normal(10,1)
Now the prior dominates, so reason as previous example but in reverse

Here's the code to reproduce:
The tail differences are easier to see on log scale. If I get some time later today, will make a version showing that.gist.github.com/rmcelreath/39d…
The tail differences are easier to see on log scale. If I get some time later today, will make a version showing that.gist.github.com/rmcelreath/39d…
• • •
Missing some Tweet in this thread? You can try to
force a refresh

 Read on Twitter
Read on Twitter