Thread by @ChristophMolnar

Which one is the better machine learning interpretation method?

LIME or SHAP?

Despite the gold rush in interpretability research, both methods are still OGs when it comes to explaining predictions.

Let's compare the giants.

Both LIME and SHAP have the goal of explaining a prediction by attributing it to the individual features. Meaning each feature gets a value.

Both are model-agnostic and work for tabular, image, and text data.

However the philosophies of how to make these attributions differ.

LIME (Local Interpretable Model-agnostic Explanations ) is a local surrogate model. Motivation: The prediction function is complex, but locally it might be nicely explained by, for example, a linear model.

LIME works by sampling data and fitting such a locally weighted model.

SHAP (SHapley Additive exPlanations ) is rooted in cooperative game theory: Each feature is seen as a team player and the prediction is the payout of a game. By simulating each player's contribution to different team constellations a "fair" distribution of the prediction.

SHAP and LIME have implementations in R and Python and lively communities. For both, you'll find tons of extensions in the forms of research papers and sometimes code.

But in the end, I'd pick SHAP over LIME.

Here are my 3 reasons:

- Neighborhood problem in LIME
- SHAP's firmer theoretic grounding
- SHAP's vast ecosystem

Both SHAP and LIME have their problems. But LIME has a problem that's a deal-breaker for me:

LIME requires local weighting with a kernel. The width of the kernel steers how local the model is. But there's no definite guide for how local the linear model should be. It's arbitrary

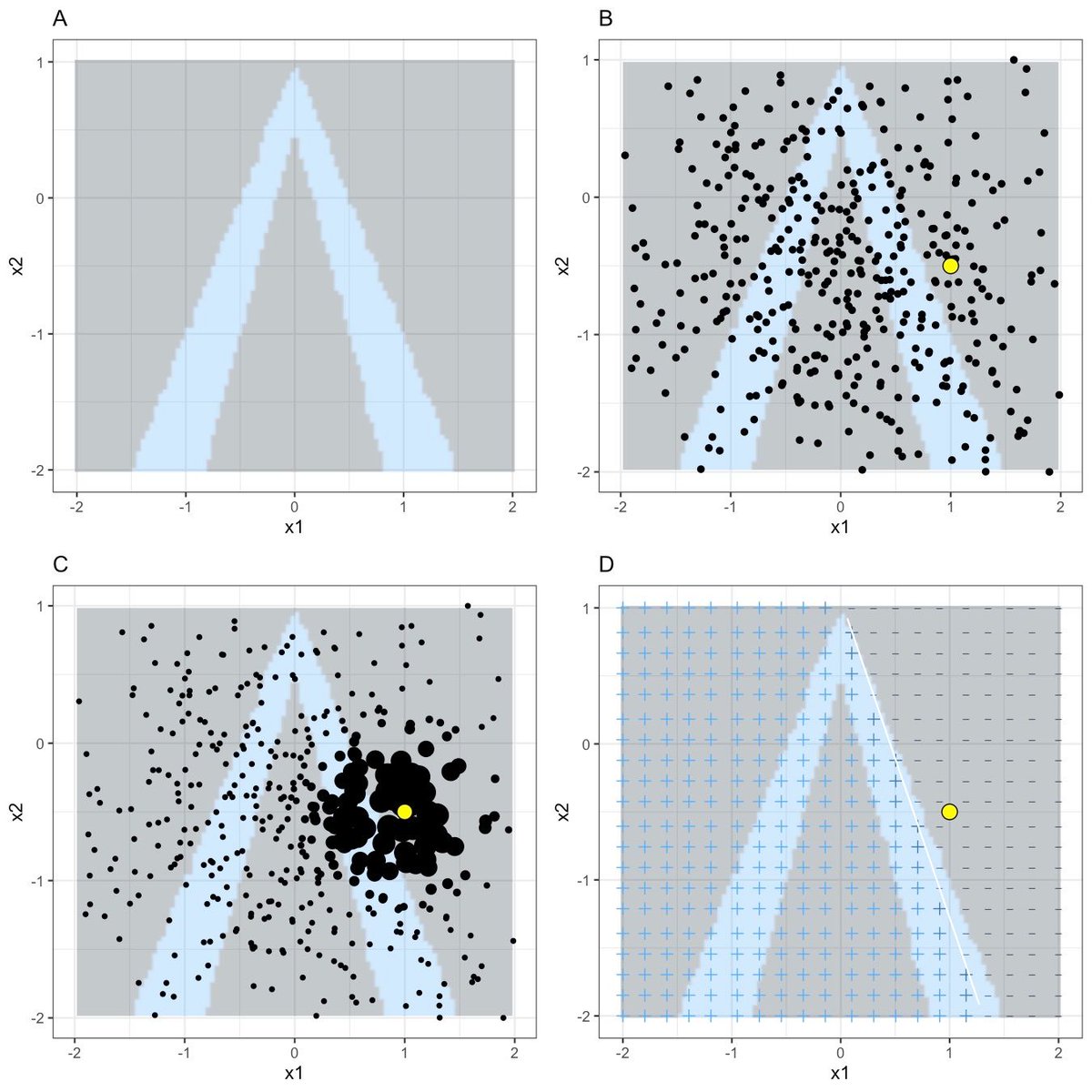
For SHAP, in contrast, it's clearly defined what the target to be estimated is: It's Shapley values from game theory. You may agree or disagree with using Shapley values for explaining predictions, but at least we know what we are dealing with.

SHAP also allows for global interpretations by aggregating the SHAP values across data points to estimate feature importances and effects, study interactions, and cluster data. In theory, you could do the same with LIME, but it's just perfectly implemented by the shap library.

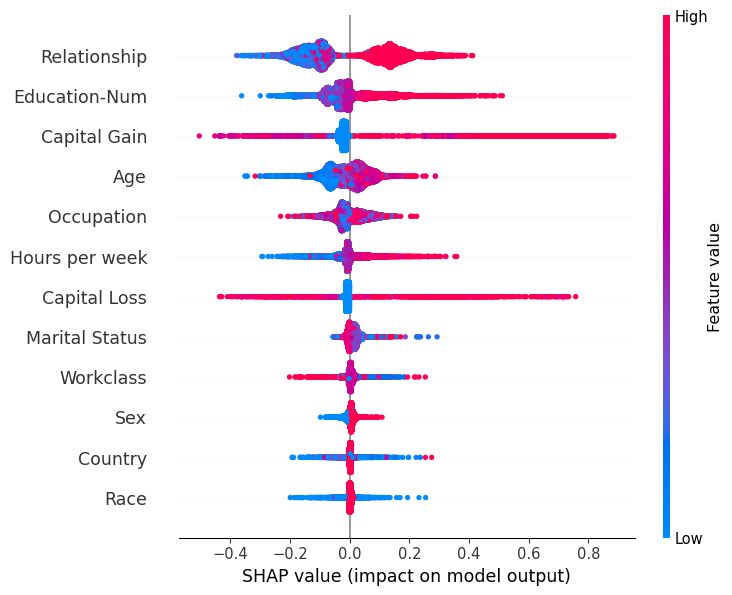
Summary: SHAP wins. LIME's neighborhood choice is too problematic. SHAP shines thanks to a vast ecosystem, global explanations, and firmer theoretical groundwork.

That's why I wrote the book Interpreting Machine Learning Models With SHAP and not with LIME.