Ayer me preguntaron "filosóficamente" por qué cuando ajustamos un modelo le pedimos ruido blanco en los residuos. Lo que viene a ser el test de Ljung Box en series temporales, por ejemplo. Rápidamente lo comento, que tengo clase en el gym jaja 

El ruido blanco es un tipo de proceso estocástico (aleatorio) caracterizado por la completa imprevisibilidad. Es algo, propiamente dicho, intrínsecamente aleatorio, que no esconde ningún tipo de patrón. No hay por dónde rascar, vaya. Nosotros, en estadística, además de inferir
relaciones causales, hacemos reconocimiento de patrones pasados para extrapolar a futuro. Esa extrapolación, no siempre posible, se da gracias a que el data science tiene no solo bases computacionales, sino una fuerte base matemática que nos permite pasar del mundo de la
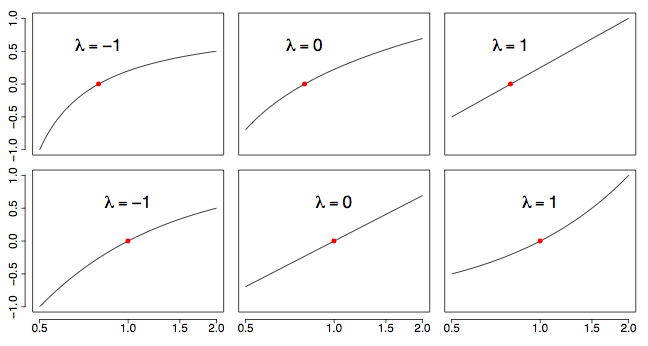
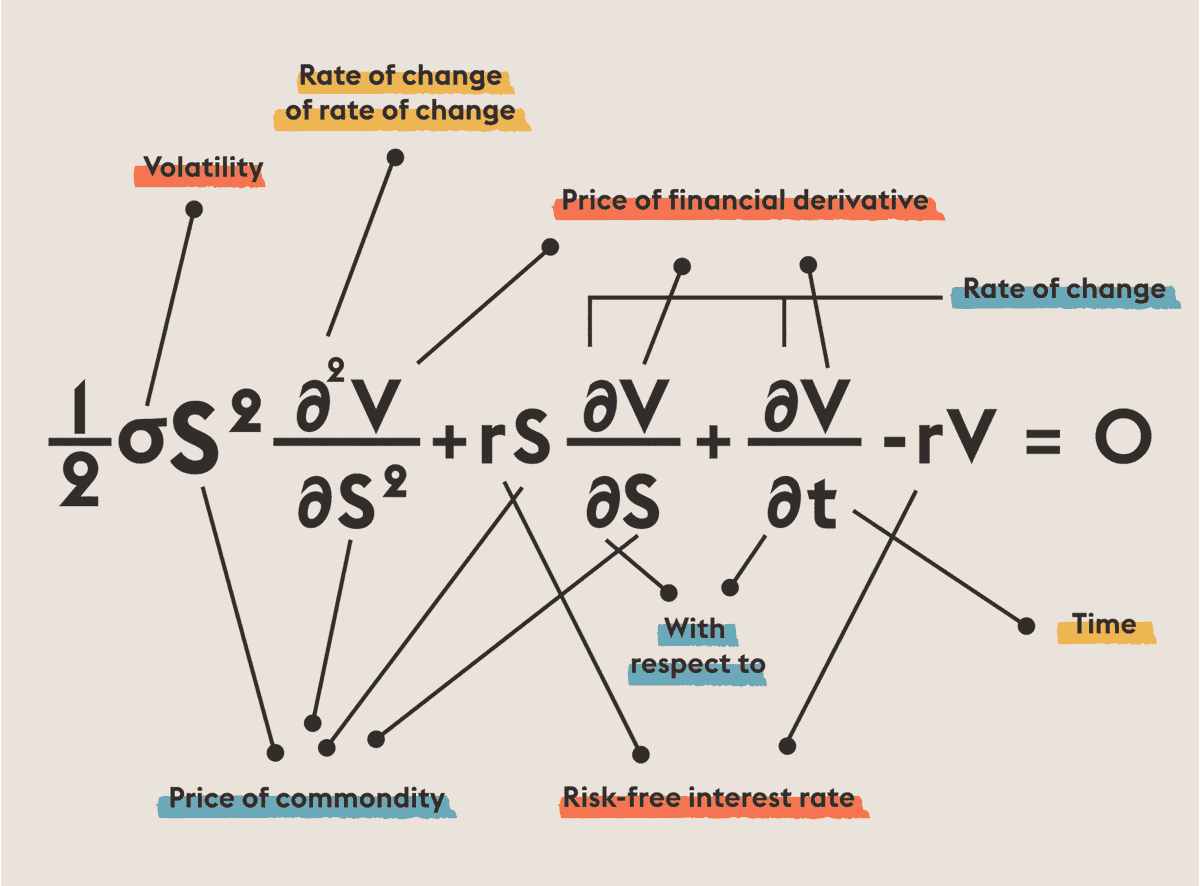
correlación al mundo de la causalidad (que en verdad es otro tipo de correlación, una correlación parcial con direccionalidad). Cuando ajustamos un modelo, siempre lo dividimos en su parte determinista y una parte aleatoria que es el error o la componente estocástica.
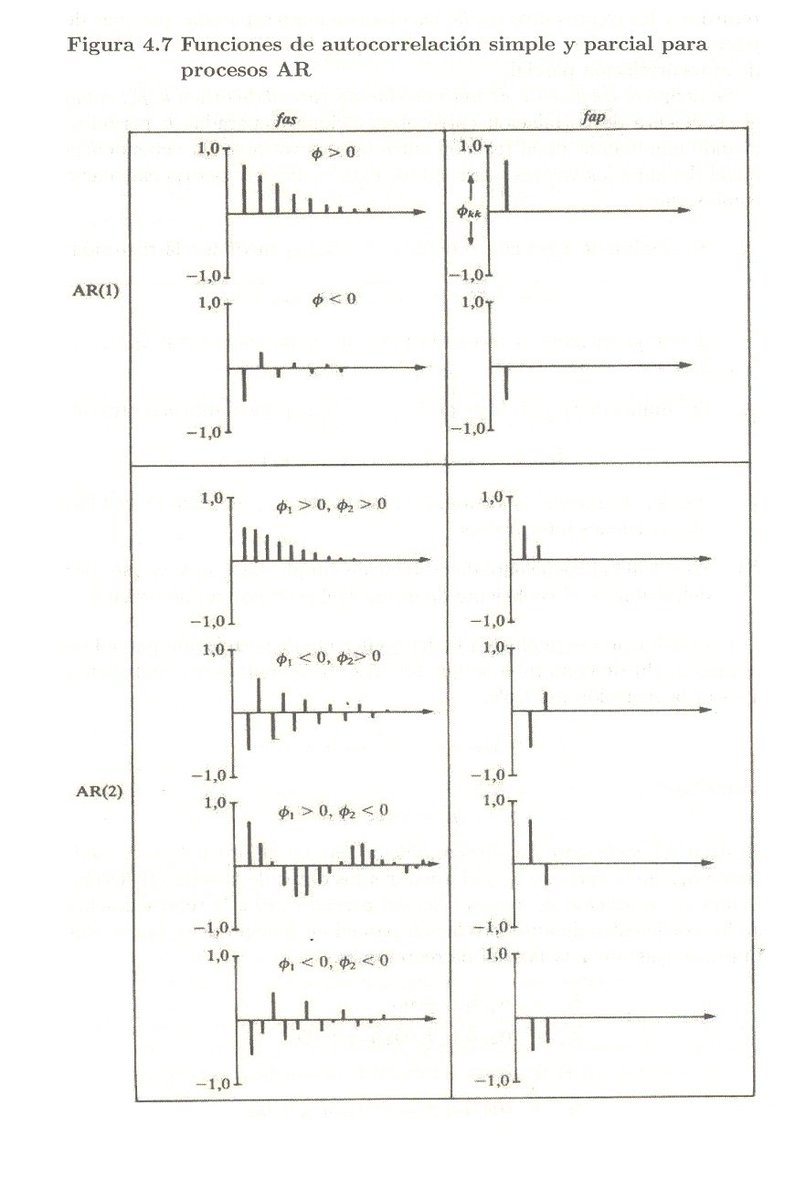
¿Qué significa que no haya ruido blanco en los residuos? Pues básicamente que en el error hay escondidos "patrones" relevantes para explicar el fenómeno de estudio, patrones que pueden contaminar la relación causal estudiada, por ejemplo, entre los regresores y el regresando.
Queremos ruido blanco porque queremos que la componente aleatoria sea eso, pura aleatoriedad sin ningún patrón. Queremos arrancarle a la componente estocástica todo lo que sea relevante. Si nos dejamos algo relevante ahí dentro, nuestro modelo estará contaminado con
correlaciones cruzadas de factores que están ahí, en el modelo, pero no explicitados. Están escondidos ahí, en el error, creando interferencias. Esta es, intuitivamente, la razón por la que el ajuste de un buen modelo pasa por conseguir ruido blanco.
• • •
Missing some Tweet in this thread? You can try to
force a refresh

 Read on Twitter
Read on Twitter