A puzzle:
Imagine you begin a journey in Seattle WA, facing exactly due east. Then start traveling forward, in a straight line along the Earth's surface.
Imagine you begin a journey in Seattle WA, facing exactly due east. Then start traveling forward, in a straight line along the Earth's surface.
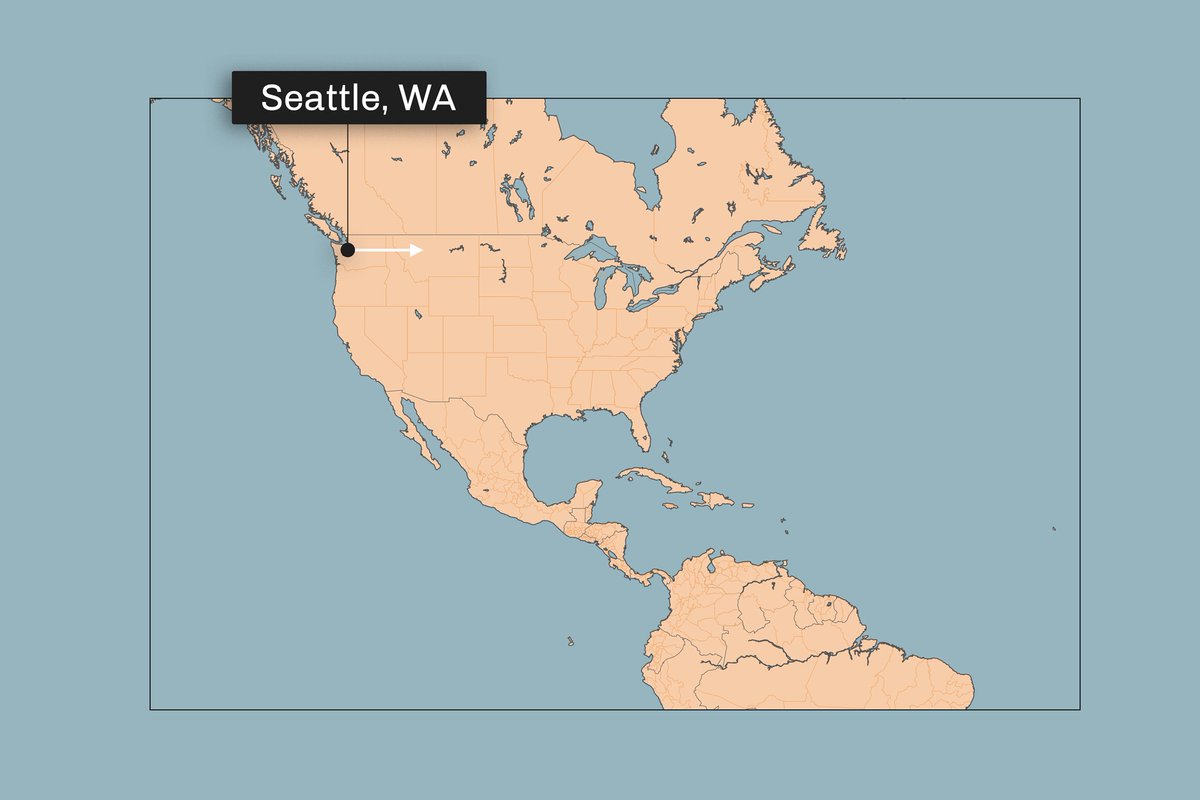
You will travel across North America, and onto the Atlantic Ocean. Eventually, you will hit another country.
What is the first country you hit?
What is the first country you hit?
⚠️ Answer below — last chance to make your own guess ⚠️
After pointing due east, and traveling continually forward in a straight line across the Earth's surface, the next country you hit after you leave North America is...
Australia.
Australia.
Ok, what's going on here?
Forget about the Earth for a second, and just imagine you're standing on a big sphere.
Point in any direction, and begin walking forward along the surface of the sphere, without changing direction.
You'll loop round and return to where you started.
Forget about the Earth for a second, and just imagine you're standing on a big sphere.
Point in any direction, and begin walking forward along the surface of the sphere, without changing direction.
You'll loop round and return to where you started.

Notice, just intuitively, how you'll have walked the full circumference of the sphere: a 'great circle'.
In order to trace out a smaller circle than that, you'd need to be constantly veering left or right.
In order to trace out a smaller circle than that, you'd need to be constantly veering left or right.
In the original puzzle, you might have been imagining traveling a line of constant latitude — that is, *always* heading east.
But that is not a great circle, and so not a straight line: you'd need to be constantly turning left to maintain that path.
But that is not a great circle, and so not a straight line: you'd need to be constantly turning left to maintain that path.

(To give an extreme example: imagine driving in a 10 meter radius around the North Pole. In order to always be traveling east — maintaining the same latitude — you'd need to be steering left the whole time)
Here's a better perspective: looking at Seattle centered on a globe, any straight line from Seattle will look like a straight line to you.
So with north pointing directly up, the path you take is a straight line directly to the right.
So with north pointing directly up, the path you take is a straight line directly to the right.

Being a great circle, exactly half of the path you travel is in the Northern Hemisphere, and half in the Southern Hemisphere. It swoops under Africa to arrive at Australia somewhere near Perth. 

I think part of the trickiness here is that straight lines on the Earth are not straight lines on most 2D projections of the Earth (maps), and vice-versa.
Which is why the shortest flight path between two cities often looks unnecessarily curved on a map.


Which is why the shortest flight path between two cities often looks unnecessarily curved on a map.


There are some exceptions: any straight line on a 'gnomonic projection' (pictured) is an arc of a great circle (straight line) on a sphere.
But how natural to think a straight line on a more familiar map is a straight line on the surface of the Earth!
But how natural to think a straight line on a more familiar map is a straight line on the surface of the Earth!

To be pedantic, by 'straight line' here I really mean 'geodesic' — the generalisation of 'straight line' for curved surfaces. but I think it's obvious enough.
If you're placed on a surface and continually walk "forward", by definition you will trace out a geodesic.
If you're placed on a surface and continually walk "forward", by definition you will trace out a geodesic.
Anyway, I hope that's clear!
I first saw this puzzle on Marc Ordower's excellent TikTok page, of all places.
I first saw this puzzle on Marc Ordower's excellent TikTok page, of all places.

• • •
Missing some Tweet in this thread? You can try to
force a refresh