1/N
This is a thread on Chhanda Shastra (छन्द शास्त्र), study of prosody, where ancient Indians invented groundbreaking mathematical concepts including binary representation, combinatorics, Pascal’s Triangle, & Fibonacci sequence at least 2000 years before they emerged in Europe
This is a thread on Chhanda Shastra (छन्द शास्त्र), study of prosody, where ancient Indians invented groundbreaking mathematical concepts including binary representation, combinatorics, Pascal’s Triangle, & Fibonacci sequence at least 2000 years before they emerged in Europe
157/N
Lagakriya (लगक्रिया) is the method that provides a solution to these type problems. It essentially computed how many different ways we can choose r objects from n of them (n > r). The modern notation used for Lagakriya is nCr
Lagakriya (लगक्रिया) is the method that provides a solution to these type problems. It essentially computed how many different ways we can choose r objects from n of them (n > r). The modern notation used for Lagakriya is nCr
158/N
Pingala gave a very terse method for computing nCr in the Chhanda Sutra. Without additional commentary, it is hard to decode this.
Pingala gave a very terse method for computing nCr in the Chhanda Sutra. Without additional commentary, it is hard to decode this.
159/N
But, we are in luck, as another genius Hindu mathematician named Halayudha Bhatta did exactly that.
But, we are in luck, as another genius Hindu mathematician named Halayudha Bhatta did exactly that.
160/N
Halayudha Bhatta wrote a commentary called Mritasanjeevani (no later than 10th century CE) on Pinagala’s Chhanda Sutra
Halayudha Bhatta wrote a commentary called Mritasanjeevani (no later than 10th century CE) on Pinagala’s Chhanda Sutra
161/N
In Mritasanjeevani, Halayudha analyzed Pinagal’s Lagakriya sutra in detail and showed how to create a table of numbers called मेरु प्रस्तार (Meru Prastara). मेरु प्रस्तार literally means an expanded mountain. The reason behind the name will be clear in the analysis below
In Mritasanjeevani, Halayudha analyzed Pinagal’s Lagakriya sutra in detail and showed how to create a table of numbers called मेरु प्रस्तार (Meru Prastara). मेरु प्रस्तार literally means an expanded mountain. The reason behind the name will be clear in the analysis below
162/N
Below I am providing the Sanskrit commentary of Halaydha on this topic
Below I am providing the Sanskrit commentary of Halaydha on this topic
163/N
Halayudha's Meru Prastara, documented no later than 10th century CE, laid the foundation for combinatorics and binomial coefficients - concepts that re-emerged in Europe nearly 700 years later as Pascal's Triangle.
Halayudha's Meru Prastara, documented no later than 10th century CE, laid the foundation for combinatorics and binomial coefficients - concepts that re-emerged in Europe nearly 700 years later as Pascal's Triangle.
164/N
It is interesting to note that the French mathematician Blaise Pascal did not invent the triangle named after him; he popularized it in Europe through his work "Traité du triangle arithmétique" (Treatise on the Arithmetical Triangle) published in 1654.
It is interesting to note that the French mathematician Blaise Pascal did not invent the triangle named after him; he popularized it in Europe through his work "Traité du triangle arithmétique" (Treatise on the Arithmetical Triangle) published in 1654.
165/N
Let’s analyze Halayudha’s commentary on Meru Prastara verse by verse starting with the first verse
Let’s analyze Halayudha’s commentary on Meru Prastara verse by verse starting with the first verse
166/N
Halayudha’s first verse gives us a method to build a pyramid-like pattern starting with a single square and adding rows, incrementing by one square per row, each extending halfway outward
Halayudha’s first verse gives us a method to build a pyramid-like pattern starting with a single square and adding rows, incrementing by one square per row, each extending halfway outward
167/N
Let’s look at Halayudha’s second verse on Meru Prastara
Let’s look at Halayudha’s second verse on Meru Prastara
168/N
In the second verse Halayudha's instructs us to start with 1 in the only square of the first row, followed by 1s in each square of the second row, and 1s at the extreme squares of every subsequent row.
In the second verse Halayudha's instructs us to start with 1 in the only square of the first row, followed by 1s in each square of the second row, and 1s at the extreme squares of every subsequent row.
169/N
Let’s look at Halayudha’s third verse on Meru Prastara
Let’s look at Halayudha’s third verse on Meru Prastara
170/N
Halayudha's third verse completed the mountain / pyramid. He asks us to start with 3s in the second row's middle squares. Each subsequent row is filled by summing the two squares directly above, representing binomial coefficients
Halayudha's third verse completed the mountain / pyramid. He asks us to start with 3s in the second row's middle squares. Each subsequent row is filled by summing the two squares directly above, representing binomial coefficients
171/N
Let’s look at Halayudha’s fourth verse on Meru Prastara
Let’s look at Halayudha’s fourth verse on Meru Prastara
172/N
In the fourth verse, Halayudha explains that the mountain or triangle represents a combinatorial framework for arranging syllables, capturing all possible patterns of short and long syllables
In the fourth verse, Halayudha explains that the mountain or triangle represents a combinatorial framework for arranging syllables, capturing all possible patterns of short and long syllables
173/N
Kedarabhatta in his seminal work Vrittaratnākara also provides specific rules to get the number of combinations of laghu (L) and Guru (L) symbols among all possible combinations of n symbols.
Kedarabhatta in his seminal work Vrittaratnākara also provides specific rules to get the number of combinations of laghu (L) and Guru (L) symbols among all possible combinations of n symbols.
174/N
The verses from Kedarabhatta’s Vrittaratnākara to calculate nCr are provided below. His method is slightly different from that of Halayudha
The verses from Kedarabhatta’s Vrittaratnākara to calculate nCr are provided below. His method is slightly different from that of Halayudha
175/N
Below I am giving a modern translation of Kedarabhatta’s verses to compute nCr along with an illustration for the case of n = 6
(the thread continues...)
Below I am giving a modern translation of Kedarabhatta’s verses to compute nCr along with an illustration for the case of n = 6
(the thread continues...)
176/N
Bhāskarāchārya(1114–1185 CE), the legendary Indian mathematician and astronomer, was centuries ahead of his time. His masterpiece Lilavati dazzled with arithmetic brilliance, while Bijaganita explored algebra like never before.
Bhāskarāchārya(1114–1185 CE), the legendary Indian mathematician and astronomer, was centuries ahead of his time. His masterpiece Lilavati dazzled with arithmetic brilliance, while Bijaganita explored algebra like never before.
177/N
In addition to other mathematical gems, Bhāskarāchārya also provided a cool method for computing binomial coefficients in his seminal work Lilavati
In addition to other mathematical gems, Bhāskarāchārya also provided a cool method for computing binomial coefficients in his seminal work Lilavati
178/N
Below I am providing translation for the above verses from Lilavati that enables us to compute nCr
Below I am providing translation for the above verses from Lilavati that enables us to compute nCr
179/N
'Sankhyā' stands for the number of possible combinations of n bits. Both Pingala and Kedarabhatta provided methods to compute 2ⁿ
'Sankhyā' stands for the number of possible combinations of n bits. Both Pingala and Kedarabhatta provided methods to compute 2ⁿ
180/N
Let’s first see how Pingala addressed computation of 2ⁿ. Below I am providing the sutras from Chapter 8 of Chhanda Sutra
Let’s first see how Pingala addressed computation of 2ⁿ. Below I am providing the sutras from Chapter 8 of Chhanda Sutra
181/N
Below I am providing translation of the above sutras along with an example
(side note: notice the usage of zero or shunya. It is one of the earliest mention of zero in the world)
Below I am providing translation of the above sutras along with an example
(side note: notice the usage of zero or shunya. It is one of the earliest mention of zero in the world)
182/N
Pingala’s iterative algorithm for computation of 2ⁿ can be summarized as
Pingala’s iterative algorithm for computation of 2ⁿ can be summarized as
183/N
Kedarabhatta in his seminal work Vrittaratnākara gave a very different approach to compute 2ⁿ
Kedarabhatta in his seminal work Vrittaratnākara gave a very different approach to compute 2ⁿ
184/N
Translation of the verse from Vrittaratnākara to compute 2ⁿ is given below
Translation of the verse from Vrittaratnākara to compute 2ⁿ is given below
185/N
Fibonacci numbers are one of the most elegant and fascinating sequences in mathematics, revealing patterns that echo throughout nature, art, and science.
Fibonacci numbers are one of the most elegant and fascinating sequences in mathematics, revealing patterns that echo throughout nature, art, and science.
186/N
It was in ancient India that this Fibonacci sequence was discovered. In fact, there has been a long tradition of mathematically analyzing this sequence in India in the context of prosody
It was in ancient India that this Fibonacci sequence was discovered. In fact, there has been a long tradition of mathematically analyzing this sequence in India in the context of prosody
187/N
Ancient Indian mathematician Virahāṅka discovered this sequence at least 500 years before Fibonacci. Another Indian mathematician Hemachandra traced this sequence to the works of Pingala which dates back to at least 300 BCE
Ancient Indian mathematician Virahāṅka discovered this sequence at least 500 years before Fibonacci. Another Indian mathematician Hemachandra traced this sequence to the works of Pingala which dates back to at least 300 BCE
188/N
Before we go into the details of the sequence, let’s talk about what exactly Fibonacci sequence is
Before we go into the details of the sequence, let’s talk about what exactly Fibonacci sequence is
189/N
This sequence begins with 0 and 1, followed by 1, 2, 3, 5, 8, 13, 21, and so on, where each number is the sum of the two preceding ones.
This sequence begins with 0 and 1, followed by 1, 2, 3, 5, 8, 13, 21, and so on, where each number is the sum of the two preceding ones.
190/N
Mathematically, the sequence is defined by the formula Fₙ = Fₙ₋₁ + Fₙ₋₂ for n >= 0 with the initial conditions F₀ = 0 and F₁=1
Mathematically, the sequence is defined by the formula Fₙ = Fₙ₋₁ + Fₙ₋₂ for n >= 0 with the initial conditions F₀ = 0 and F₁=1
191/N
Fibonacci numbers appear widely in nature, such as in the spirals of shells, seed arrangements in flowers, and the branching of trees.
Fibonacci numbers appear widely in nature, such as in the spirals of shells, seed arrangements in flowers, and the branching of trees.
192/N
They have inspired applications across disciplines, including art, architecture, music, and computer algorithms, showcasing their deep mathematical significance.
They have inspired applications across disciplines, including art, architecture, music, and computer algorithms, showcasing their deep mathematical significance.
193/N
Remarkably, the ratio of consecutive Fibonacci numbers approaches the Golden Ratio (𝜙 ≈ 1.618), a constant celebrated for its connection to beauty and harmony.
Remarkably, the ratio of consecutive Fibonacci numbers approaches the Golden Ratio (𝜙 ≈ 1.618), a constant celebrated for its connection to beauty and harmony.
194/N
The Fibonacci numbers are embedded within Pascal’s Triangle. When the diagonals of Pascal’s Triangle (which was also invented in India as shown in this thread) are summed, they form Fibonacci numbers.
The Fibonacci numbers are embedded within Pascal’s Triangle. When the diagonals of Pascal’s Triangle (which was also invented in India as shown in this thread) are summed, they form Fibonacci numbers.
195/N
Named after the Italian mathematician Leonardo of Pisa, known as Fibonacci, these numbers were introduced to Europe in his book Liber Abaci published in 1202 CE
Named after the Italian mathematician Leonardo of Pisa, known as Fibonacci, these numbers were introduced to Europe in his book Liber Abaci published in 1202 CE
196/N
It is important to point out the deep impact of Indian mathematics on Fibonacci’s work. I am providing an excerpt written by Fibonacci from the book “Liber Abaci”
It is important to point out the deep impact of Indian mathematics on Fibonacci’s work. I am providing an excerpt written by Fibonacci from the book “Liber Abaci”
197/N
Fibonacci acknowledged India as the origin of a profound mathematical system (including its decimal system), noting its use among Egyptians, Syrians, Greeks, and Sicilians.
Fibonacci acknowledged India as the origin of a profound mathematical system (including its decimal system), noting its use among Egyptians, Syrians, Greeks, and Sicilians.
198/N
Recognizing its superiority over older, error-prone methods, Fibonacci mentioned that he adopted the Indian mathematical approach with insights from Euclidean geometry
Recognizing its superiority over older, error-prone methods, Fibonacci mentioned that he adopted the Indian mathematical approach with insights from Euclidean geometry
199/N
From now on, we will refer to the Fibonacci sequence as the Virahāṅka-Hemachandra sequence, honoring the rich legacy of Indian mathematicians and prosodists who originally discovered it.
From now on, we will refer to the Fibonacci sequence as the Virahāṅka-Hemachandra sequence, honoring the rich legacy of Indian mathematicians and prosodists who originally discovered it.
200/N
Today what we know as Fibonacci sequence was originally discovered by the great Indian mathematician Virahāṅka (no later than 600 CE) & elaborated later by another genius mathematician Hemachandra (no later than 1100 CE)
(the thread continues...)
Today what we know as Fibonacci sequence was originally discovered by the great Indian mathematician Virahāṅka (no later than 600 CE) & elaborated later by another genius mathematician Hemachandra (no later than 1100 CE)
(the thread continues...)
201/N
Virahanka (विरहाङ्क) was a brilliant Indian prosodist and mathematician. He is believed to have composed his seminal work Vrattajati Samuccaya (वृत्तजातिसमुच्चय:) no later than 600 CE.
Virahanka (विरहाङ्क) was a brilliant Indian prosodist and mathematician. He is believed to have composed his seminal work Vrattajati Samuccaya (वृत्तजातिसमुच्चय:) no later than 600 CE.
202/N
Virahanka’s contributions to prosody expanded upon Pingala’s Chhanda-sutras (no later than 300 BCE). His work later served as the foundation for Gopala’s 12th-century commentary.
Virahanka’s contributions to prosody expanded upon Pingala’s Chhanda-sutras (no later than 300 BCE). His work later served as the foundation for Gopala’s 12th-century commentary.
203/N
So far in this thread we have worked with meters that are of type "Varna Vritta". It refers to a meter based on the specific arrangement of letters (varnas), where the pattern of light (Laghu) and heavy (Guru) syllables within a line is predetermined
So far in this thread we have worked with meters that are of type "Varna Vritta". It refers to a meter based on the specific arrangement of letters (varnas), where the pattern of light (Laghu) and heavy (Guru) syllables within a line is predetermined
204/N
"Matra Vritta" refers to a meter based on the duration of syllables (morae), where the number of "matras" (metrical units) in a line is fixed, with the syllable count also being important.
"Matra Vritta" refers to a meter based on the duration of syllables (morae), where the number of "matras" (metrical units) in a line is fixed, with the syllable count also being important.
205/N
Matra Vritta focuses on the timing of syllables, while Varna Vritta focuses on the specific letter combinations used in a line
Matra Vritta focuses on the timing of syllables, while Varna Vritta focuses on the specific letter combinations used in a line
206/N
Virahanka-Hemachandra sequence is related to the concept of Matra Vritta
Virahanka-Hemachandra sequence is related to the concept of Matra Vritta
207/N
Matra Vritta which enables metrical poetry based on syllabic duration was briefly touched upon by Pingala in the context of Arya and Vaitaliya meters. However, it gained prominence in Prakrit and regional Indian languages.
Matra Vritta which enables metrical poetry based on syllabic duration was briefly touched upon by Pingala in the context of Arya and Vaitaliya meters. However, it gained prominence in Prakrit and regional Indian languages.
208/N
Virahanka (विरहाङ्क) provided a comprehensive explanation of matra vrittas in his work Vrittajati Samuccaya (वृत्तजातिसमुच्चय:). He introduced mathematical techniques to list and count meters based on matras.
Virahanka (विरहाङ्क) provided a comprehensive explanation of matra vrittas in his work Vrittajati Samuccaya (वृत्तजातिसमुच्चय:). He introduced mathematical techniques to list and count meters based on matras.
209/N
The key question Virahanka addressed in this regard was “How many poetic meters are possible for a quarter having n matras? And how can we list all such meters?”
The key question Virahanka addressed in this regard was “How many poetic meters are possible for a quarter having n matras? And how can we list all such meters?”
210/N
Below I am providing the sutras from Vrittajati Samuccaya that deal with the solution to this above problem. The method is called Mātrā Prastāra (मात्रा प्रस्तार)
Below I am providing the sutras from Vrittajati Samuccaya that deal with the solution to this above problem. The method is called Mātrā Prastāra (मात्रा प्रस्तार)
211/N
Here is a modern translation of the Virahanka’s Mātrā Prastāra method
Here is a modern translation of the Virahanka’s Mātrā Prastāra method
212/N
Let’s construct a Mātrā Prastāra for a quarter having 4 matras using Virahanka’s method
Let’s construct a Mātrā Prastāra for a quarter having 4 matras using Virahanka’s method
213/N
Now let’s construct a Mātrā Prastāra for a quarter having 5 matras using Virahanka’s method
Now let’s construct a Mātrā Prastāra for a quarter having 5 matras using Virahanka’s method
214/N
Finally let’s construct a Mātrā Prastāra for a quarter having 6 matras using Virahanka’s method
Finally let’s construct a Mātrā Prastāra for a quarter having 6 matras using Virahanka’s method
215/N
Let’s closely observe how the Mātrā Prastāra unfolds when n = 6. The last column of the first 5 rows (rows 1–5) contains all G
Let’s closely observe how the Mātrā Prastāra unfolds when n = 6. The last column of the first 5 rows (rows 1–5) contains all G
216/N
Since the value of G = 2, the remaining columns in these rows must add up to 4 matras.
Since the value of G = 2, the remaining columns in these rows must add up to 4 matras.
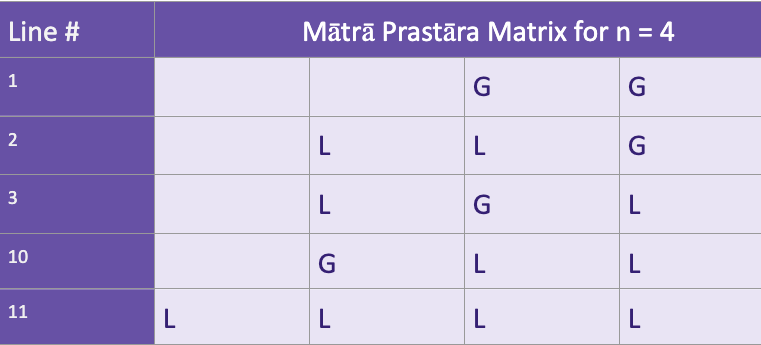
217/N
The remaining columns must follow the Prastāra for n = 4 matras. When you compare with the Prastāra table for n = 4, you’ll find that it exactly matches.
The remaining columns must follow the Prastāra for n = 4 matras. When you compare with the Prastāra table for n = 4, you’ll find that it exactly matches.
218/N
Now let’s analyze rows 6 to 13. The last column here contains all Ls. Since the value of L = 1, the remaining columns in these rows must add up to 5 matras.
Now let’s analyze rows 6 to 13. The last column here contains all Ls. Since the value of L = 1, the remaining columns in these rows must add up to 5 matras.
219/N
This means the remaining columns must follow the Prastāra for n = 5 matras. When you compare with the Prastāra table for n = 4, you’ll find that it exactly matches.
This means the remaining columns must follow the Prastāra for n = 5 matras. When you compare with the Prastāra table for n = 4, you’ll find that it exactly matches.
220/N
So, how do we count the total number of poetic meters for n = 6 matras? For n = 6, we observe:
S₆ = S₅ + S₄
So, how do we count the total number of poetic meters for n = 6 matras? For n = 6, we observe:
S₆ = S₅ + S₄
221/N
For any Prastāra with n matras, rows end with either:
G (2 matras) - Remaining columns must add up to n - 2.
Or
L (1 matra) - Remaining columns must add up to n - 1.
For any Prastāra with n matras, rows end with either:
G (2 matras) - Remaining columns must add up to n - 2.
Or
L (1 matra) - Remaining columns must add up to n - 1.
222/N
This leads to a beautiful recurrence relation: Sₙ = Sₙ₋₁ + Sₙ₋₂
Does this remind you of something? Yes, it’s the Fibonacci sequence hidden in poetry!
This leads to a beautiful recurrence relation: Sₙ = Sₙ₋₁ + Sₙ₋₂
Does this remind you of something? Yes, it’s the Fibonacci sequence hidden in poetry!
223/N
Virahanka explained this in his Sankhya Pratyay as follows and he identifies the numbers in the series as simply “Sankhyanka”
Virahanka explained this in his Sankhya Pratyay as follows and he identifies the numbers in the series as simply “Sankhyanka”
224/N
This gives us the following sequence of Virahanka’s Sankhyankas (सङ्ख्यांक) as a function of n
This gives us the following sequence of Virahanka’s Sankhyankas (सङ्ख्यांक) as a function of n
225/N
This gives us the following sequence of Virahanka’s Sankhyankas (सङ्ख्यांक) as a function of n
(the thread continues...)
This gives us the following sequence of Virahanka’s Sankhyankas (सङ्ख्यांक) as a function of n
(the thread continues...)
226/N
Hemacandra, one of the greatest Indian Jaina mathematicians, provided in-depth analysis of the numbers of variations of mātrā-vṛttas in his brilliant book Chandonuśāsana (no later than 1140 CE)
Hemacandra, one of the greatest Indian Jaina mathematicians, provided in-depth analysis of the numbers of variations of mātrā-vṛttas in his brilliant book Chandonuśāsana (no later than 1140 CE)
227/N
Like Virahanka, rather than counting meters based on a fixed number of syllables, Hemachandra analyzed meters with a fixed duration, assigning one beat to short syllables and two beats to long syllables
Like Virahanka, rather than counting meters based on a fixed number of syllables, Hemachandra analyzed meters with a fixed duration, assigning one beat to short syllables and two beats to long syllables
228/N
The number of possible patterns follows the sequence 1, 2, 3, 5, 8, 13, 21. . ., where each term is obtained by summing the two preceding terms.
The number of possible patterns follows the sequence 1, 2, 3, 5, 8, 13, 21. . ., where each term is obtained by summing the two preceding terms.
229/N
Here is an excerpt from chapter 8, section 16 & 17 from Chandonuśāsana by Hemachandra that provides description of how to analyze mātrā-vṛttas and in the process documents the numbers that is today known as Fibonacci sequence
Here is an excerpt from chapter 8, section 16 & 17 from Chandonuśāsana by Hemachandra that provides description of how to analyze mātrā-vṛttas and in the process documents the numbers that is today known as Fibonacci sequence
230/N
The 'Prākṛita-Paiṅgalaṃ' (composed no later than 1300 CE) is one of the most important documents on Prosody which is well known for its comprehensive treatment of Prākṛit and Apabhraṃśa meters, recording not only their definitions, but also copious illustrations
The 'Prākṛita-Paiṅgalaṃ' (composed no later than 1300 CE) is one of the most important documents on Prosody which is well known for its comprehensive treatment of Prākṛit and Apabhraṃśa meters, recording not only their definitions, but also copious illustrations
231/N
Prākṛita-Paiṅgalaṃ shows the connection between Virahanka-Hemachandra numbers & Pingala’s Meru Prastāra.
Prākṛita-Paiṅgalaṃ shows the connection between Virahanka-Hemachandra numbers & Pingala’s Meru Prastāra.
232/N
The author of Prākṛita-Paiṅgalaṃ demonstrated that the Virahanka-Hemachandra numbers are, in fact, sums of numbers on certain diagonals in the Meru Prastāra computed by Pingala
The author of Prākṛita-Paiṅgalaṃ demonstrated that the Virahanka-Hemachandra numbers are, in fact, sums of numbers on certain diagonals in the Meru Prastāra computed by Pingala
233/N
We will now look into brilliant work done by Nārāyaṇa Paṇḍita (1356 CE) in the field of Prosody.
We will now look into brilliant work done by Nārāyaṇa Paṇḍita (1356 CE) in the field of Prosody.
234/N
Nārāyaṇa Paṇḍita was a renowned mathematician of medieval India, celebrated for his profound contributions to arithmetic, algebra, and combinatorics.
Nārāyaṇa Paṇḍita was a renowned mathematician of medieval India, celebrated for his profound contributions to arithmetic, algebra, and combinatorics.
235/N
His masterpiece, Gaṇitakaumudī (The Moonlight of Mathematics), revolutionized combinatorics by generalizing earlier works on permutations, combinations, and enumerations, bridging practical applications with abstract mathematical principles.
His masterpiece, Gaṇitakaumudī (The Moonlight of Mathematics), revolutionized combinatorics by generalizing earlier works on permutations, combinations, and enumerations, bridging practical applications with abstract mathematical principles.
236/N
Complementing this, his Bījagaṇita Vātāṃsa (The Garland of Algebra) delved into algebraic equations and indeterminate analysis, showcasing his deep mathematical insight.
Complementing this, his Bījagaṇita Vātāṃsa (The Garland of Algebra) delved into algebraic equations and indeterminate analysis, showcasing his deep mathematical insight.
237/N
Nārāyaṇa Paṇḍita deserves a special mention in this thread because he treated the combinatorics problems with a broad mathematical viewpoint, generalizing and unifying many of the earlier results.
Nārāyaṇa Paṇḍita deserves a special mention in this thread because he treated the combinatorics problems with a broad mathematical viewpoint, generalizing and unifying many of the earlier results.
238/N
Specifically, Nārāyaṇa Paṇḍita considered prastāras of syllabic meters with more than two types of syllables generalising the work of Piṅgala, prastāras of permutations with repetitions generalising the work of Śārṅgadeva on svara-prastāra
Specifically, Nārāyaṇa Paṇḍita considered prastāras of syllabic meters with more than two types of syllables generalising the work of Piṅgala, prastāras of permutations with repetitions generalising the work of Śārṅgadeva on svara-prastāra
239/N
Nārāyaṇa Paṇḍita also generalized prastāras of combinations which were considered earlier by Varāhamihira (c. 550 AD) and Bhaṭṭotpala (c. 950 AD)
Nārāyaṇa Paṇḍita also generalized prastāras of combinations which were considered earlier by Varāhamihira (c. 550 AD) and Bhaṭṭotpala (c. 950 AD)
240/N
Nārāyaṇa Paṇḍita presents a brilliant generalization of the mātrā-vritta, which we will analyze in some depth here
Nārāyaṇa Paṇḍita presents a brilliant generalization of the mātrā-vritta, which we will analyze in some depth here
241/N
Nārāyaṇa extended earlier methods by allowing elements beyond binary values (L and G), introducing sequences with values 1, 2, …, q.
Nārāyaṇa extended earlier methods by allowing elements beyond binary values (L and G), introducing sequences with values 1, 2, …, q.
242/N
Instead of using laghus and gurus, Nārāyaa considers sequences of variable length p formed from the digits 1, 2,.. . q where q is the highest or the last digit, such that their total value or sum n is fixed.
Instead of using laghus and gurus, Nārāyaa considers sequences of variable length p formed from the digits 1, 2,.. . q where q is the highest or the last digit, such that their total value or sum n is fixed.
243/N
To explore the different patterns in the generalized mātrā-vritta-prastāra, Nārāyana introduces a range of sequences and tabular structures at the beginning of his chapter on combinatorics
To explore the different patterns in the generalized mātrā-vritta-prastāra, Nārāyana introduces a range of sequences and tabular structures at the beginning of his chapter on combinatorics
244/N
One of the most important sequences he describes is the sāmāsikī-pankti (additive sequence), which generalizes the Virahāṅka-Hemachandra sequence.
One of the most important sequences he describes is the sāmāsikī-pankti (additive sequence), which generalizes the Virahāṅka-Hemachandra sequence.
245/N
It plays a key role in calculating the saṅkhyā, or the total number of rows, in the prasthāra. In verses 13–14 of the Ankapaśa chapter of Gaitakaumudī, Nārāyana defines the sāmāsikī-pankti in detail.
It plays a key role in calculating the saṅkhyā, or the total number of rows, in the prasthāra. In verses 13–14 of the Ankapaśa chapter of Gaitakaumudī, Nārāyana defines the sāmāsikī-pankti in detail.
246/N
Below I am providing a translation of sāmāsikī-pankti by Nārāyaṇa Paṇḍita
Below I am providing a translation of sāmāsikī-pankti by Nārāyaṇa Paṇḍita
247/N
Here is sāmāsikī-pankti by Nārāyaṇa Paṇḍita using modern notation
Here is sāmāsikī-pankti by Nārāyaṇa Paṇḍita using modern notation
248/N
So, Nārāyaṇa Paṇḍita provided a method to generate a general purpose sequence for which Virahāṅka-Hemachandra sequence (later known as Fibonacci sequence) becomes a special case
So, Nārāyaṇa Paṇḍita provided a method to generate a general purpose sequence for which Virahāṅka-Hemachandra sequence (later known as Fibonacci sequence) becomes a special case
249/N
Now let's wrap up this thread
Now let's wrap up this thread
250/N
Chhanda Shastra (छन्द शास्त्र) - the ancient Indian study of prosody - reveals groundbreaking concepts, including binary representation, combinatorics, Pascal’s Triangle, and the Fibonacci sequence, developed in India at least 2000 years before their emergence in Europe
Chhanda Shastra (छन्द शास्त्र) - the ancient Indian study of prosody - reveals groundbreaking concepts, including binary representation, combinatorics, Pascal’s Triangle, and the Fibonacci sequence, developed in India at least 2000 years before their emergence in Europe
251/N
Chhanda Shastra is not just the heartbeat of Sanskrit poetry - it is a testament to the mathematical and philosophical genius of ancient India. Through patterns of sound and rhythm, it encodes truths that transcend language, bridging art and computation.
Chhanda Shastra is not just the heartbeat of Sanskrit poetry - it is a testament to the mathematical and philosophical genius of ancient India. Through patterns of sound and rhythm, it encodes truths that transcend language, bridging art and computation.
252/N
From combinatorics to recursion, the echoes of Chhanda resonate through modern mathematics and computer science, reminding us that algorithms once flowed from verses, and elegance was measured in syllables.
From combinatorics to recursion, the echoes of Chhanda resonate through modern mathematics and computer science, reminding us that algorithms once flowed from verses, and elegance was measured in syllables.
253/N
The genius of Chhanda lies in how ancient Indian scholars fused the realms of music, linguistics, and computation into a single, harmonious framework - transforming patterns of sound into algorithms and verses into mathematical blueprints.
The genius of Chhanda lies in how ancient Indian scholars fused the realms of music, linguistics, and computation into a single, harmonious framework - transforming patterns of sound into algorithms and verses into mathematical blueprints.
254/N
May we continue to uncover and honor the depth of this ancient Indian legacy - where poetry met precision, and imagination shaped infinity.
May we continue to uncover and honor the depth of this ancient Indian legacy - where poetry met precision, and imagination shaped infinity.
255/N
References
References
• • •
Missing some Tweet in this thread? You can try to
force a refresh
