Thread by @gf_256

In 2020, I solved a gnarly reverse engineering challenge in PlaidCTF. Only 9 teams solved.

It's a huge pile of Typescript. Everything is named after a fish.

The catch? There's no code, only types. How do they perform computation using just the type system?

(Spoiler: Circuits!)

Let's break this down into individual lines, at least.

That's better. We can even see some constants. But almost every type uses other types, that we still don't understand.

Let's try sorting all the lines by length, shortest to longest. That should put the simplest definitions first, so we can reverse it from the bottom up.

Now look at Dogfish. It's the first non-trivial type that isn't a constant.

Swordfish is true, Ponyfish is false, and Dogfish is an algebraic type that must satisfy both True and False; e.g., the null type never.

We can check this in a REPL:

Aha: They're using the type system itself to do computation. The types constrain what values belong to them. By doing computations on types, we can do arbitrary computation!

So this challenge is (ab)using the type system's Turing-completeness to build a flag checker!

Uh oh. I have a bad feeling about this.

First though, let's figure out how some primitive "gadgets" they use everywhere.

Here's how they check whether two types are equal, by abusing the extends operator:

type Equ = X extends Y ? (Y extends X ? True : False) : False;

I.e.: "If X ⊆ Y and Y ⊆ X, then X = Y".

Next is how they implement Car and Cdr from Lisp.

Here's how Car and Cdr work. Given a pair (tuple of 2 elements), Car gives you the first element. Cdr gives you the second element.

Can you see how it works?

What they're doing is extremely clever. It's pattern matching on the args of a dummy functional type. That's how they represent a tuple. Then, Car (Cdr) peels off the first (second) arg of a "…" expansion. The ... is like Python *args.

That's how they destructure a tuple.

If you thought that was crazy, wait till you see this.

Then they use Car and Cdr with tail recursion to accomplish iteration. This is how they check if two binary numbers are equal:

There’s a lot going on here.

It creates a dict and then indexes into it. It’s kind of like a switch statement. The dict part is responsible for either recursing or returning the base case. The index does combinatorial logic for what to do based on the current recursion level.

Our BinNums are essentially representations of integers in binary form, with LSB at the front of the array and MSB at the end.

So this “function” takes in two BinNums, and returns if they are equal by iterating through the bits in order and checking if they are all equal.

Remember everything is actually a type: our functions are conditional types. Our parameters are actually type parameters. Our numbers are actually just types representing arrays of binary digits.

To make this concrete, let me give an example.

Correct computations typecheck!

So this is basically building up bit-level computation. The types set up a circuit, and valid evaluations of the circuit type check.

The flag checker is implemented in this circuit, and we need to (1) reverse how logic is implemented in circuit form; then (2) reverse the logic.

Now you may be wondering... that's great but how can we do arithmetic? How do we add two BinNums?

Well...using a full adder of course :-)

What about bitwise arithmetic?

We can even build a multiplier!

Here is how they index into a list. They do this by recursively skipping every other element based on the bits of the index (!!!)

Keep in mind, all of these identifiers and strings were just names of fish.

So I was sitting there discovering how "Tuna" is actually a ripple-carry adder.

I was feeling pretty good at this point. I was understanding what everything was doing.

But then my heart sank when I saw this.

Can you guess what this does?

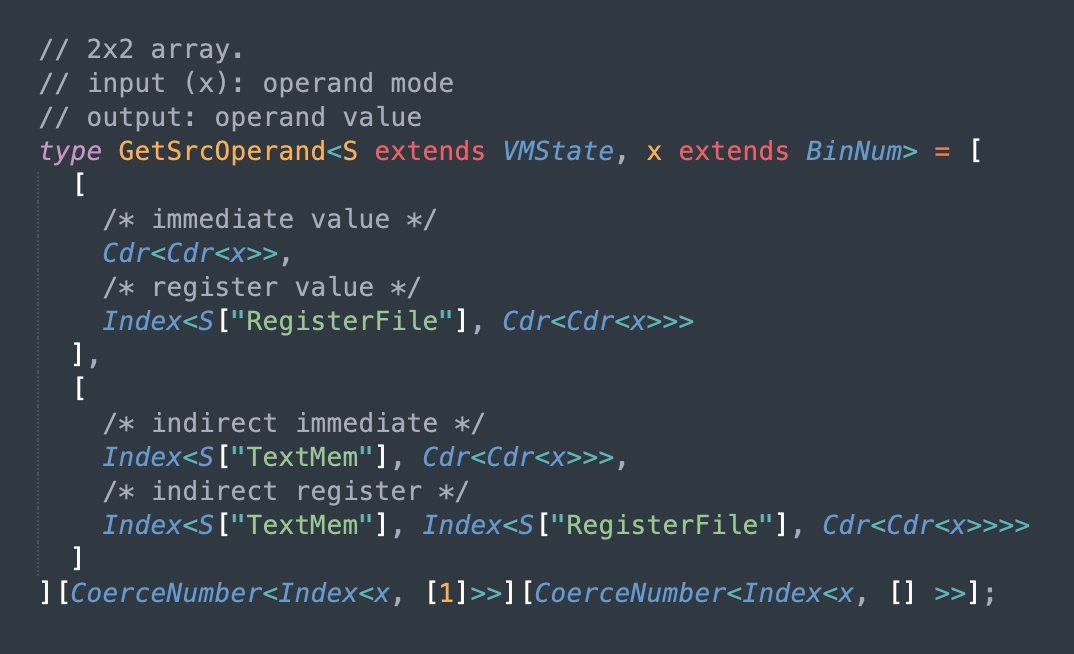
Yup... this is implementing computing the operand value for an instruction. Oh boy... this is probably going to be an entire RISC CPU.

RISC processors often fetch operand values during the instruction decode stage, and that's what's going on here.

Guess what! It's a virtual machine.

Here's the full processor state. It also implements binary heaps built in which is very very quirky.

Again, keep in mind every name here used to be the name of a fish🫠 This is all manually renamed

And here's the instruction set.

And here's how they actually launch the VM and check the flag with it. They pass the flag as input to the VM (the VM code is parameterized by the input; the VM is parameterized by the code)

Essentially, this entire VM is used as a type constraint on our input!

Meaning, the type system, not any interpreted code, checks our input! The computation is done in this circuit, that is executed through type checking.

It initializes a VM state using our input, then applies StepVM until the VM halts and returns a scalar. This scalar is the VM’s exit code (halt state). This final state is asserted to be zero. So our flag needs to satisfy this whole circuit.

And the big array of binary digits we saw in the very first screenshot is actually the VM’s bytecode.

Now, if you disassemble the bytecode, you'll realize there's control flow... even subroutines and functions!

Here's a screenshot from the Binary Ninja plugin @hgarrereyn independently wrote as part of his solve.

@hgarrereyn If you translate this to pseudocode, it basically implements this check:

@hgarrereyn This is asking us to find a permutation of (xs, ys) that results in the Manhattan distances between consecutive points sums to 0x470.

This is essentially finding a Hamiltonian cycle of specified length!

@hgarrereyn This is a NP complete problem, but luckily we can attack this with dynamic programming. My teammate Sampriti wrote a solver and it gave the solution
[0,9,15,2,1,4,3,8,10,5,13,11,14,6,7,12,0]

And if we feed this into the challenge, we actually get our flag!

@hgarrereyn I really enjoyed this challenge. This thread was excerpted from the full writeup, which you can find here: blog.perfect.blue/Lot-of-Fish-Pl…

@hgarrereyn Lastly:

We're sponsoring @PlaidCTF this year at Zellic. This is a lifelong dream of mine. Thank you so much to the organizers for putting on such an excellent CTF each year!

PlaidCTF will be running starting this Friday. Sign up here:

Cheers! plaidctf.com