Assortative mating and preferences towards intelligence -- a short criticism of a common argument
There's an argument that regularly pops up here. It goes something like:
A: "Men don't care about intelligence."
B: "The data says otherwise, intelligent men marry intelligent women."
Here I won't argue that B is wrong per se, but more that the argument or evidence provided as counter-argument isn't good.
First, we should recognize that there are two parties in a marriage. In theory, this assortative mating could be entirely driven by smart women's preferences to marry educated and smart men. (Not saying this is the case, but the symmetry of the correlation means that assortative mating doesn't tell us *whose* preference is operating)
Second -- and my more serious criticism -- is that assortative mating can arise for reasons other than preferences. In particular, society is stratified in terms of intelligence, and it might just arise because smart people live and partake in certain environments.
Smart people tend to mingle with other smart people. They meet, and sometimes form relationships. That could explain why smart people marry other smart people, without any need for any overt preference for intelligence.
I want to make this point clear: even if smart people had zero preference towards intelligence, you'd expect substantial assortative mating in terms of education/intelligence simply because of how people indirectly sort themselves throughout society.
This is not merely a "what-if" philosophical objection. There is a compelling Norwegian study which shows that the majority of the educational assortative mating can be explained by the fact that people tend to meet in specific institutions they attend (Kirkebøen, Leuven & Mogstad, 2021).
My point was not to disprove that (intelligent) men prefer intelligent women. It's more a call for people to think about the issues more carefully and present more compelling evidence either way.
There's an argument that regularly pops up here. It goes something like:
A: "Men don't care about intelligence."
B: "The data says otherwise, intelligent men marry intelligent women."
Here I won't argue that B is wrong per se, but more that the argument or evidence provided as counter-argument isn't good.
First, we should recognize that there are two parties in a marriage. In theory, this assortative mating could be entirely driven by smart women's preferences to marry educated and smart men. (Not saying this is the case, but the symmetry of the correlation means that assortative mating doesn't tell us *whose* preference is operating)
Second -- and my more serious criticism -- is that assortative mating can arise for reasons other than preferences. In particular, society is stratified in terms of intelligence, and it might just arise because smart people live and partake in certain environments.
Smart people tend to mingle with other smart people. They meet, and sometimes form relationships. That could explain why smart people marry other smart people, without any need for any overt preference for intelligence.
I want to make this point clear: even if smart people had zero preference towards intelligence, you'd expect substantial assortative mating in terms of education/intelligence simply because of how people indirectly sort themselves throughout society.
This is not merely a "what-if" philosophical objection. There is a compelling Norwegian study which shows that the majority of the educational assortative mating can be explained by the fact that people tend to meet in specific institutions they attend (Kirkebøen, Leuven & Mogstad, 2021).
My point was not to disprove that (intelligent) men prefer intelligent women. It's more a call for people to think about the issues more carefully and present more compelling evidence either way.
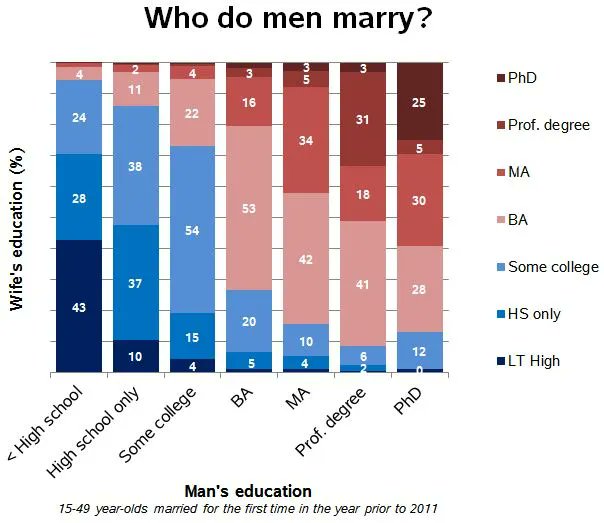
The graph:
familyinequality.wordpress.com/2013/04/04/edu…
The Norwegian study:
ssb.no/en/forskning/d…
familyinequality.wordpress.com/2013/04/04/edu…
The Norwegian study:
ssb.no/en/forskning/d…
• • •
Missing some Tweet in this thread? You can try to
force a refresh




















