Thread by @prathyvsh

Creating an infocomic to journal about my understanding of Lambda Calculus. I hope to reorganize this to create a structured product at some point in the future. But for now, here is what I have:

Lambda Calculus was invented by Alonzo Church as a response to Entscheidungsproblem posed by Hilbert and Ackermann. But let us bother ourselves with $2 technical words. Instead let us see Lambda Calculus as a tool to explore computational space and see where that notion takes us.

To understand a framework, we need to start from the fundamentals. We will start by using colors as the primitives for our exploration of Lambda Calculus.

Correction: Let us *not* bother. Computer Science and Mathematics is chockfull of technical words that are quite a mouthful but when you peek behind the curtains, you can see them to be really straightforward ideas that emerged in different contexts (of solving problems).

This is an easy and accessible introduction to Lambda Calculus (with a linguist slant) by @david2vec: imgur.com/a/XBHub

@david2vec List of math publications reviewed by Alonzo Church (the guy who invented Lambda Calculus) during his 43 year career in chairing the Journal of Symbolic Logic. It includes papers on Neural Nets, Kleene's recursive functions, Theology, Von Neumann's Quantum logic and more!

@david2vec A WIP screenshot of making sense out of the research I'm doing for this project. This is a good metaphor for the research — I need to put a lot of interlinked ideas together, study their connection, pick them apart and then put them back together to make sense.

@david2vec Computing is both a means and an end in itself. Former gives us the wonderful engineering artefacts and latter helps us understand the logic of life. It's a shame that we have very little people in the intersection of both to unify practice with theory and vice versa.

@david2vec Awesome to behold the braids of history. McCulloch and Pitts worked on understanding the logic of biological neural activity inspired from Turing's work. This work was used by Von Neumann in his EDVAC draft which birthed "stored program" computers:

https://twitter.com/prathyvsh/status/1162166080569335808

@david2vec What is odd about later developments in computer science is that this field which weaved together the three threads of biology, physics, and logic closely in one braid got ravelled into mutually exclusive disciplines that lost sight of original unity.

https://twitter.com/prathyvsh/status/1185025647011188736

@david2vec What we now have is a comedy/tragedy (depending on your perspective) where we have logicians in ivory towers far removed from day to day concerns of engineering; engineers not bothered with the theory because who cares; and God knows where to find a scientist engaged in both.

@david2vec Here are two visual representations of Lambda Calculus I found in the wild:

https://twitter.com/prathyvsh/status/1191384318620291072

There's also a survey + dissertation by @bntr: bntr.planet.ee/lambda/work/vi… and a really curious take on it by @mbuliga: imar.ro/~mbuliga/graph…

@david2vec @bntr @MBuliga Stories of the past are not ones with a fixed meaning but rather acquires dynamic meaning in the light of future events. This is evident in Hilbert's famous Entscheidungsproblem: en.wikipedia.org/wiki/Entscheid… that took on a new formulation after Gödel's incompleteness theorem.

@david2vec @bntr @MBuliga Paper on Logic, Arithmetic, and Automata by Alonzo Church accompanying the lecture he delivered in 1962. I haven't figured out the relevance of this one yet, but something tells me its significant for making sense of Church's oeuvre.

@david2vec @bntr @MBuliga Learnt that Alan Turing intended to build a machine to calculate Riemann Zeta Function. This is how the blueprint looks like. Source: turingarchive.org/viewer/?id=118…

At this point, I have learnt up some amount of historical antecedents leading to the creation of Lambda Calculus. Understood the core abstractions used to build the system and I am making an attempt to create a running system to interact with the mathematical structures.

For this purpose I have started looking at the Meta II paper:

https://twitter.com/prathyvsh/status/1195059983399804929?s=21

and I am adopting WebAssembly as the target language. An initial look at this gives me a feel that things arent going to be as straightforward as I thought.

A nice quote I found in this journey.

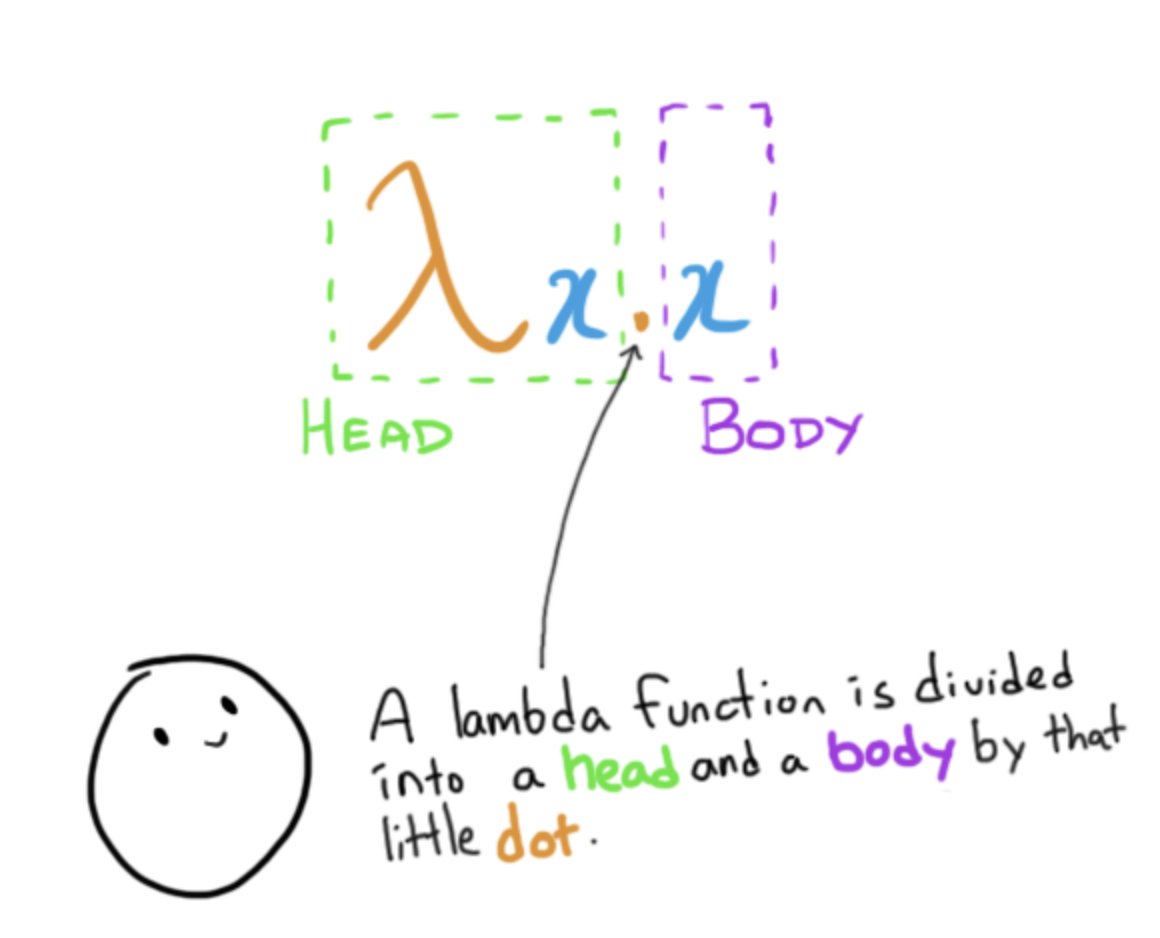
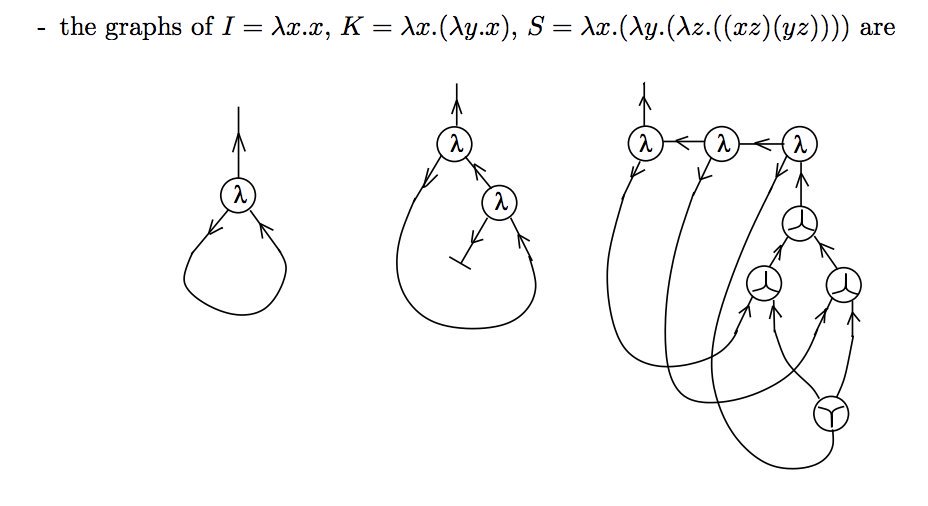
From J. Barkley Rosser: en.wikipedia.org/wiki/J._Barkle…

Source: cs.umd.edu/~gasarch/BLOGP… A paper that argues against being too formal with programming languages.

I would have something to talk about a new form of learning I am converging towards: "Understanding the present by remembering stories of the past". This articulation is sparked by two people who recently came into the picture when learning about compilers and lambda calculus.

Learnt about Alick Glennie when reading Meta II paper and stumbled on Christopher Strachey again when I was researching virtual machines to compile Lambda Calculus. What I learnt this time around was that both of them were friends of Alan Turing.

Glennie and Turing worked on Mark 1 and created an AI chess program together: chessgames.com/perl/chessgame…

Christopher Strachey, co-inventor of CPL and denotational semantics studied in King’s College with Alan Turing. Strachey would later reach out to Turing for Mark 1's handbook.

Stretch goal for this project: Implement this Draughts program (1951) by Strachey for Pilot ACE (Computer designed by Alan Turing) using a visual canvas and lambda calculus: historyofinformation.com/detail.php?id=…

Created this timeline/timebraid on how Alan Turing and peers collaborated to create Computer Science as we know it today!

Throughout this quest, I am coming to appreciate how history is not this linear one damn thing after another as popularly conceptualized but parallel threads of cross-pollination of ideas. They braid together promiscuously to create a new status quo.

Reading history of logic has helped me in slowly building a narrative framework of the intellectual history starting from a medieval monk Llull → Leibniz → Frege → Hilbert, Russell → Church, Turing → Kleene → McCarthy, Landin → now.

Here is a visualization of this story:

Using this as a tapestry, weaving in the stories of Gleick, Strachey, and Landin's collaboration into this becomes easy:

https://twitter.com/prathyvsh/status/1197525794245009408

I now perceive what is happening as a meaningful unfolding story of humans collectively building up the idea of computation.

Its only half a page of this paper on History of Lambda Calculus by Barkley Rosser and he has already made me examine the way functions work inside a computer closer. He puts forth the idea that all functions are operationally unary even when defined as multi-arity.

As the research deepens what I'm bumping against now is the opposition of Aristotelianism vs. Augustinism in Middle Age philosophical thought:

https://twitter.com/prathyvsh/status/1207313250733314050

Augustinian thought emphasized non-mechanizable intuition over Aristotelian mechanizable empiricism.

The characteristic number idea introduced by Leibniz here feels like a hidden link between logical transitivity and arithmetic/algebraic commutativity of multiplication on numbers: pron.github.io/posts/computat…

In terms of conceptual leaps, Gottfried Leibniz single handedly made significant contributions to the field of computation: Characteristica Universalis + idea of logical computation + built a mechanical computer + formalized binary arithmetic.

And all these ~350 years ago!

TIL in early days, algebra used to be known as “Universal Arithmetic”.

Source: A Treatise on Algebra by George Peacock (1830) — one of the early treatise on symbolic approach to algebra archive.org/details/atreat… /via pron.github.io/posts/computat…

Interesting to note that in 1840s Babbage's algebra was speculated to turn powerful enough to express the structure and function of human body — its “muscles, integuments, membranes &c.” and “functions of respiration, digestion, and assimilation”.

Source: pron.github.io/posts/computat…

A recurrent idea I bump on in this research is that some of the well-known mathematical systems emerged out of religious beliefs. George Boole, inventor of Boolean Algebra, as an ecumenist who rebelled against the Trinity worship of his time.

Source: pron.github.io/posts/computat…

This take on mathematical systems emerging out from faith based thought is outlined in the history of Victorian era Mathematics by Daniel J. Cohen: amzn.to/2NeEDKD

Boole’s original algebra had a notion of time which seems to be curiously missing in modern treatments. Unearthing these sort of subtle details that are brushed under the rug for fitting the cast of modern treatises is a good reason to go prospecting the history of a field.

TIL about Automated Mathematician: en.wikipedia.org/wiki/Automated…, a discovery system written in Lisp by Douglas Lenat (of Cyc fame) via Douglas Hofstadter's foreword to Gödel’s Proof:

Dana Scott’s recollection of how Lambda Calculus gets recycled every decade is well worth a watch for the personal anecdotes he shares. There’s also this instance of absurdity where he shares why the symbol ”Lambda” in Lambda Calculus was chosen :

https://twitter.com/prathyvsh/status/1026069704090107906

If you follow the threads of evolution of technology closely in different domains, say linguistics and logic in this case, one can’t help but find a sort of consilience among disparate seeming domains. Here is Frege replacing subject/predicate by argument/function dichotomy:

This ties together with the idea that there are links among disparate ideas appearing throughout the computational universe:

https://twitter.com/prathyvsh/status/1152945019071766528

Cf. Montague quantification (linguistics) has connections to continuations (functional programming): en.wikipedia.org/wiki/Montague_…

I’d be compiling and serializing this stories of computation into a browsable website up next. Collecting materials for research, feel free to suggest any articles/books you think would enrich the narrative this way:

https://twitter.com/prathyvsh/status/1198085261281779712?s=20

Robin Gandy, student of Turing, on ”the uncluttered mind”. If you are an entrant to the field of logic/scientific inquiry, it could be tempting to see this as an encouragement to forego learning about literature of a field to go at it with a “fresh mind”, but this could be naïve.

Alan Turing was a generalist and read widely on very different topics. He was fluent in German and up-to-date in the mathematical advances of his time as can be seen in the references of his paper:

https://twitter.com/prathyvsh/status/1168766689460150278

Gödel who produced a proof for God’s existence: en.wikipedia.org/wiki/G%C3%B6de… claimed Turing’s notion of computation as philosophically erroneous to model human cognition. Kleene rejected it as a “pie in the sky”.

Source: pron.github.io/posts/computat…

Finished this erudite three part essay on the history of intersection between computation, logic, and algebra by @pressron. I highly recommend this series to those interested in the history of computation: pron.github.io/posts/computat…

@pressron Conjecture: Alan Turing knew a thing or two about Poincare’s embezzlement at the three body problem of late 19th century: en.wikipedia.org/wiki/Three-bod… (or one of the related threads) which inspired him to answer the Entscheidungsproblem in the negative: en.wikipedia.org/wiki/Entscheid…

@pressron Pretty interesting essay on type theory by @mrkgrnao here: colimit.net/posts/normalis… Breaks down the more complex concepts to their composites and gives interesting metaphors to ground them.

@pressron @mrkgrnao Definition of types by Benjamin Pierce from his classic TAPL: amzn.to/31SzuOQ

Source: blog.steveklabnik.com/posts/2010-07-…

Defunctionalization technique is a nifty idea to optimize code execution by retaining the contextual knowledge: gresearch.co.uk/article/defunc…

As I explore this further, I sense that a lot of ideas in compiler design is yet to make it to mainstream programming, particularly frontend.

This stems from my deep seated belief that UI design is actually compiler construction under the hood. What a designer achieves by designing an interaction language is creating a ground for interpretation from user input to pixel grid transformations mirroring what compilers do.

This is a perspective that is heard very less in programming circles! Lambda Calculus is NOT functional programming:

https://twitter.com/wcrichton/status/1245080533966585856

Peter Landin and Dana Scott apparently learnt of Lambda Calculus from Paul Rosenbloom’s book: The Elements of Mathematical Logic (1950).

As seen in the footnote from Michael Mahoney’s paper on computation: rutherfordjournal.org/article030107.…

Interaction animation of ZX-Calculus done by @konstantinosmei is pure gold. Wish visual programming environments had this kind of #🧃 h/t @Westoncb @maxkriegers

https://twitter.com/konstantinosmei/status/1254083811064909824

Reading upon the history of Lattice theory today and apparently Boole, Peirce, and Schröder in Logic and Dedekind in Number Theory are the ones who brought legitimacy to this field of study.

Source:

https://twitter.com/prathyvsh/status/1258537300780175361

Difference in the takes of Schröder and Peirce is outlined. The work done by Schröder would then go on to influence the work of Post via his book on Logic that Post read resulting in the work on Post’s Lattice: en.wikipedia.org/wiki/Post%27s_…

More detail:

https://twitter.com/prathyvsh/status/1256317540705263616

Dedekind’s work on Number Theory yielded more general structures. He invented “dual groups” (lattices) that are modules of rings. Modularity being a weakened form of distributivity.

Garrett Birkhoff coined the word “lattice”: en.wikipedia.org/wiki/Garrett_B… and his work apparently spearheaded modern developments.

Completed Gödel’s Proof by Nagel & Newman. It is a neat exposition for the curious layman. But in order to make it short and accessible for laity, they paid the cost by compromising on the structure and intricacies of the original presentation.

https://twitter.com/prathyvsh/status/1224280673629786112

Ideas in Gödel’s proof (book):

1/ The proof is very much a finite vs. in(de)finite thing

2/ Many popular accounts that refer it are over-simplifying and using it for erroneous conclusions (Example: Gödel proved that logic is inconsistent!)

3/ Gödel called for Platonic realism

I recommend reading the N&N book if you are intrigued about what Gödel’s Proof entail and why it is of huge philosophical import. But I intensely feel that if you want to do creative work with it, that 🧃 is to be found in the nuances of the original: amzn.to/3bkABK9

Before I started this journey to make a Visual Lambda Calculus Explorer, my intuitions were guiding me to create a projection of the linguistic Lambda expressions. But what I slowly realized as I went ahead in this journey is that Lambda Calculus is inherently a visual entity.

My functional programming education was done with HtDP: github.com/prathyvsh/htdp and I was aware of the link between Lambda Calculus and Lisps. Having ASTs in their unadorned form enables creation of tree visualizations. I made this little proposal for a Scheme editor in 2015.

Tree editors are a common alternative when you explore the Lisp/functional programming landscape. Some examples are:

1/ Cirru: cirru.org
2/ Lamdu: lamdu.org
3/ Luna (DAGs): luna-lang.org
4/ Pure Data (DAGs): puredata.info

Now I keep hearing about Lambda Calculus as something worthy of great admiration in the functional programming circles and decide to investigate. Half true stories like MCarthy based Lisp on Lambda Calculus accentuates this:

https://twitter.com/wcrichton/status/1155898240753000449

I dig into Lambda Calculus, only to find myself in a community of practice that greatly values symbolic rune reading and manipulation. As an illustration, here is how you increment 1 to obtain 2 in Lambda Calculus.

Symbols of Lambda Calculus are a patterning devoid of any meaning themselves but stand together to create a new level of meaning. Let us see how this can be enacted with emojis. Here’s an Emoji Lambda Calculus:

Lambda Calculus seen in a way is a method to create meaningful constructs out of intrinsically meaningless patterns. Arrangements are chosen so as to create a semantically meaningful mapping on a meta layer. This is much akin to the “duality of patterning” idea in linguistics.

What I also figured out as I learnt more about Lambda Calculus is that the linguistic constructs and their evolutionary growth (trace) can be cast visually as tree structures.

In Lambda Calculus, successive evaluations to obtain redexes can be thought of as the evolution of a tree structure. Viewed from this perspective, the trace of this evaluation results in a forest of these trees.

Created a catalog of Visual Lambda Calculi: github.com/prathyvsh/lamb…

Found out two new books about Gödel’s Proof:

1/ Raymond Smullyan’s exposition: amzn.to/3bCcMxm

2/ Gödel’s Theorem — An Incomplete Guide to Its Use and Abuse: amzn.to/3607dYD This one addresses the unwarranted extrapolations seen in pop media. h/t @AlexanderKatt

Here is a collection of documents I am using to understand the history of Lambda Calculus: github.com/prathyvsh/hist…

One more resource for easily understanding Gödel’s proof — A Simple Exposition of Gödel’s Theorem by J. R. Lucas: users.ox.ac.uk/~jrlucas/Godel…

He made it so that first year undergrad students could understand it.

If you can make your way around the reductio ad absurdum conclusion of this post, it is a pretty accessible intro to grok what Kolmogorov complexity in the context of programming languages is: forwardscattering.org/post/7

A nice talk by Philip Wadler retelling the story of computability theory. An interesting part w.r.t. this thread thus far is how Church, Gödel, and Alan Turing each came up with a formalization of computability and all three were proved to be equivalent:

A realization with Curry-Howard correspondence: en.wikipedia.org/wiki/Curry%E2%… is that you get to see program evaluation is theorem proving. It is most evident in functional programming, with a stepper, you can see the same kind of tree evolution in logic:

https://twitter.com/prathyvsh/status/1260972217598271489

So a programmer can be thought of as transforming and arriving at certain computational structures and curating the ones that are meaningful for humans at the interaction level. And this corresponds directly to proof structures which signify theorems on a different plane.

Isomorphisms via Curry Howard Correspondence runs deeper. Here is a list of correspondences between logic and type theory from Wadler’s talk:

Found out about a programming language called Automath by Nicolaas Govert De Bruijn: en.wikipedia.org/wiki/Automath Funny thing is he discovered the Curry-Howard correspondence independently in this work.

Visualization of boolean operators as grid cells allows for studying their symmetries.

There is a notation called Randolf Diagrams which is used to denote boolean operators: en.wikipedia.org/wiki/Randolph_…

Here is McCullough (the co-inventor of artificial neurons) using them on a blackboard:

https://twitter.com/prathyvsh/status/1190645765036597250

Pretty intriguing article on computing with tiles: moyix.wordpress.com/2012/04/06/com…

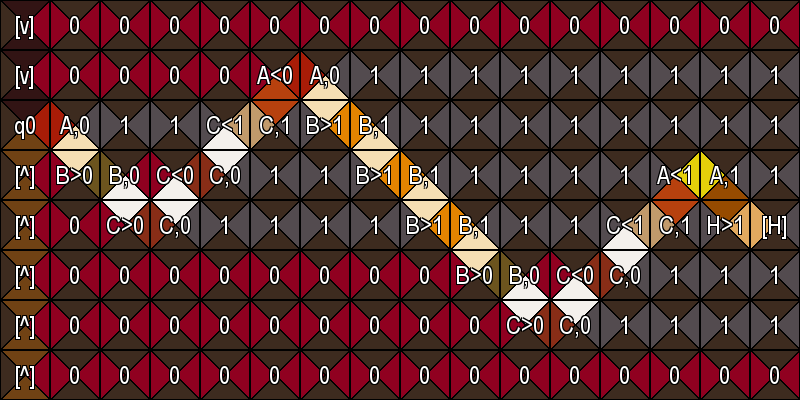
Second image is the trace of a Turing machine performing the busy beaver program represented using Wang tiles.

Found out a neat schema of different logical notations used for the 16 boolean operators:

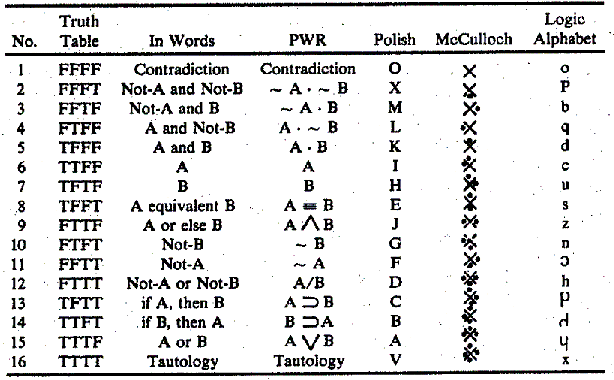
Source: logic-alphabet.net/notation_syste…

Really interesting to page through manuscripts of Charles Peirce. This guy has done some real notation design work. Here is him talking about the “likjo form” from his “The Simplest Mathematics”.

The manuscripts are available from the Harvard archive: hollis.harvard.edu/primo-explore/…

Finished reading “A Boolian Algebra with One Constant” by Peirce: rs.cms.hu-berlin.de/peircearchive/…

He builds up a minimal notational system in which a true assertion is expressed as P and it’s negation as PP. Elimination and development of these propositions is then conducted.

Going over through Huntington’s Sets of Independent Postulates for the Algebra (1904): archive.is/9NgN2 and can see some diagrams where a truth table notation is employed.

Came across this remarkable unpublished paper by Henry Sheffer on creating an invariant notational system that generalizes relative notations called “The General Theory of Notational Relativity”.

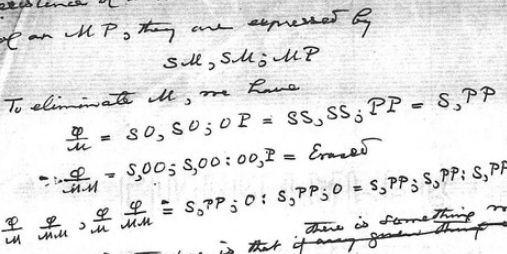
I downloaded it from HathiTrust and put it on this repo: github.com/prathyvsh/hist…

Just realized that all variables can be cast as a function:

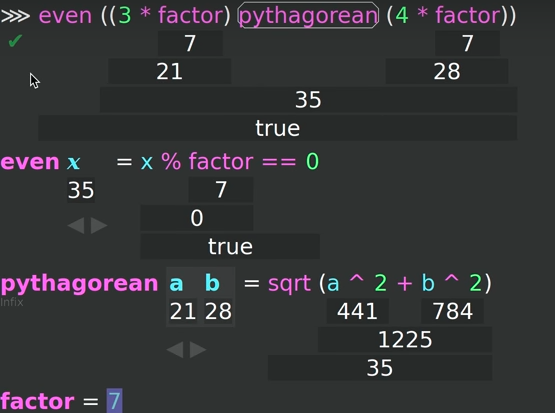
let x = 3; is equivalent to def x() => 3;

What is the use? This means, if you are after a language basis with least amount of primitives, you can do away with variables and just use functions like in Lambda Calculus.

Markov used the eponymous chains for analyzing Pushkin’s poetry! archive.vn/BBNum

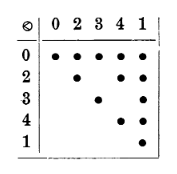
He wanted to show how interdependent samples converge to a stable configuration corresponding to the long term average behaviour of the system.

First figure from: archive.is/aVN4j

When you peruse the history of Mathematics, you come across a lot of great ideas that were ahead of their time. A classic example is how Grassmanian algebras were dismissed at the time but found application in quantum mechanics, 100 years later.

Stumbled on the work of Kneale and Kneale on “The Development of Logic”: amzn.to/2BQsWHX If you are interested in the history of logic, I am slowly accumulating the resources I come across in my explorations in this Git repo: github.com/prathyvsh/hist…

This idea of working on an idea over a long period with versioned open notes, I think is a good way to capture and communicate your research progress to others and your future self: github.com/prathyvsh/hist…

Wish research environments supported versioning of notes.

Learnt about this archbishop, Richard Whately who revived logic in England during the 19th Century. He influenced the work of Boole, DeMorgan, Jevons, and Peirce. His “Elements of Logic (1827)” was used as a textbook in prominent universities of the time: en.wikipedia.org/wiki/Richard_W…

Three ideas that have strong parallels in focussing on a thing as content and context:

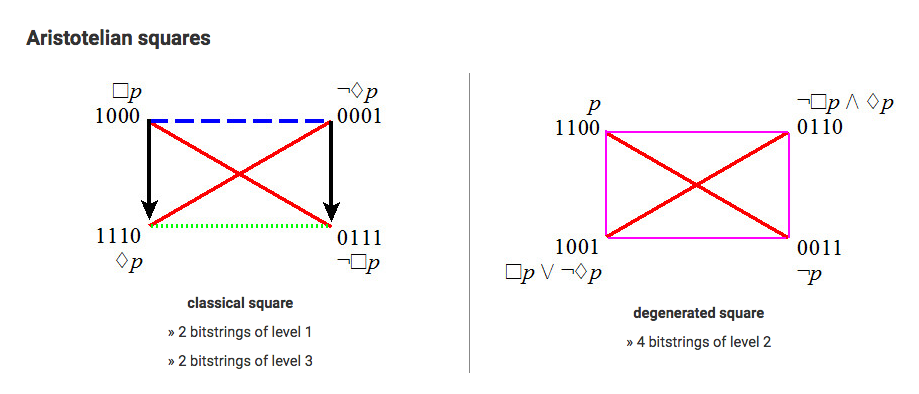
1/ Yoneda Lemma: en.wikipedia.org/wiki/Yoneda_le…

2/ The Pragmatic Maxim of Peirce: en.wikipedia.org/wiki/Pragmatic…

3/ Leibniz’ Compossibility: en.wikipedia.org/wiki/Compossib…

Church—Turing thesis is an as of yet unproven thesis on effective calculability. In my research so far I have ran across two lines of works that questions it’s validity:

1/ Robert Rosen’s work on (M, R) systems: link.springer.com/article/10.100…
2/ Yuri Gurevich’s: arxiv.org/abs/1901.04911

Stumbled on this website that represents Aristotle’s syllogisms using bit strings: logicalgeometry.org/diagrams/two_d…

Christopher Alexander famously had this affinity graph on the tradeoffs that happen with design choices in constructing a system. Think it would be a neat idea to plot mathematicians like this with their affinity to *-isms like Platonism, Empiricism, Logicism, Formalism etc.

Use quotes from their works that show agreement/conflict with each belief system (*-ism) and one can obtain a large network graph that can be partitioned algorithmically to acquire the least connected networks which suggests a picture of characteristic systems of thought.

But as Alexander rightly notes, if you attempt to acquire a picture of influences among systems of thought, what you’ll get is the shaded region of dependencies which will be unlike most algorithmically driven least network partitions.

Density of links can’t be evidenced as an indicator of influence between systems of thought. What is needed is at least a dynamic map of interactions: how people’s ideas got influenced over a lifetime as they assimilated and responded to compatible and contradictory theories.

Serendipitous discovery of the day. Connection between Lambda Calculus and the 4-Color Problem from graph theory!

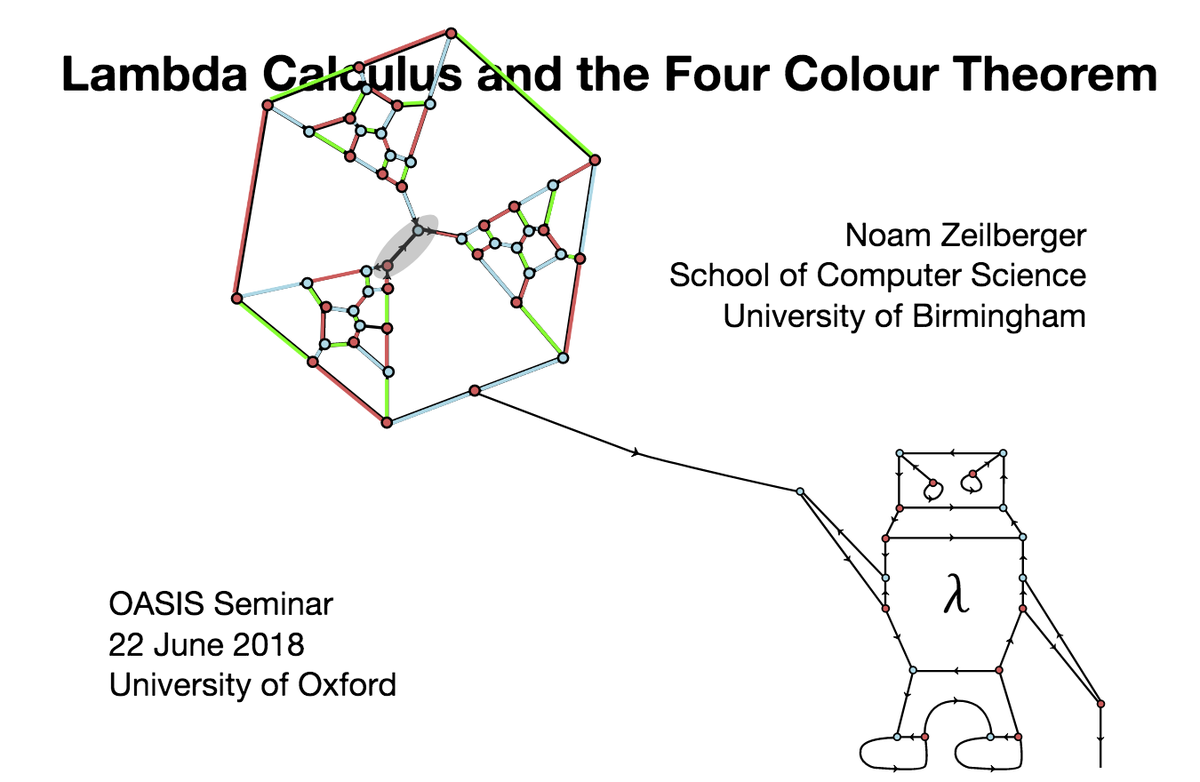
Slides here: cs.bham.ac.uk/~zeilbern/talk…

Cool Lambda Calculus map drawer by @jcreed: jcreedcmu.github.io/demo/lambda-ma…

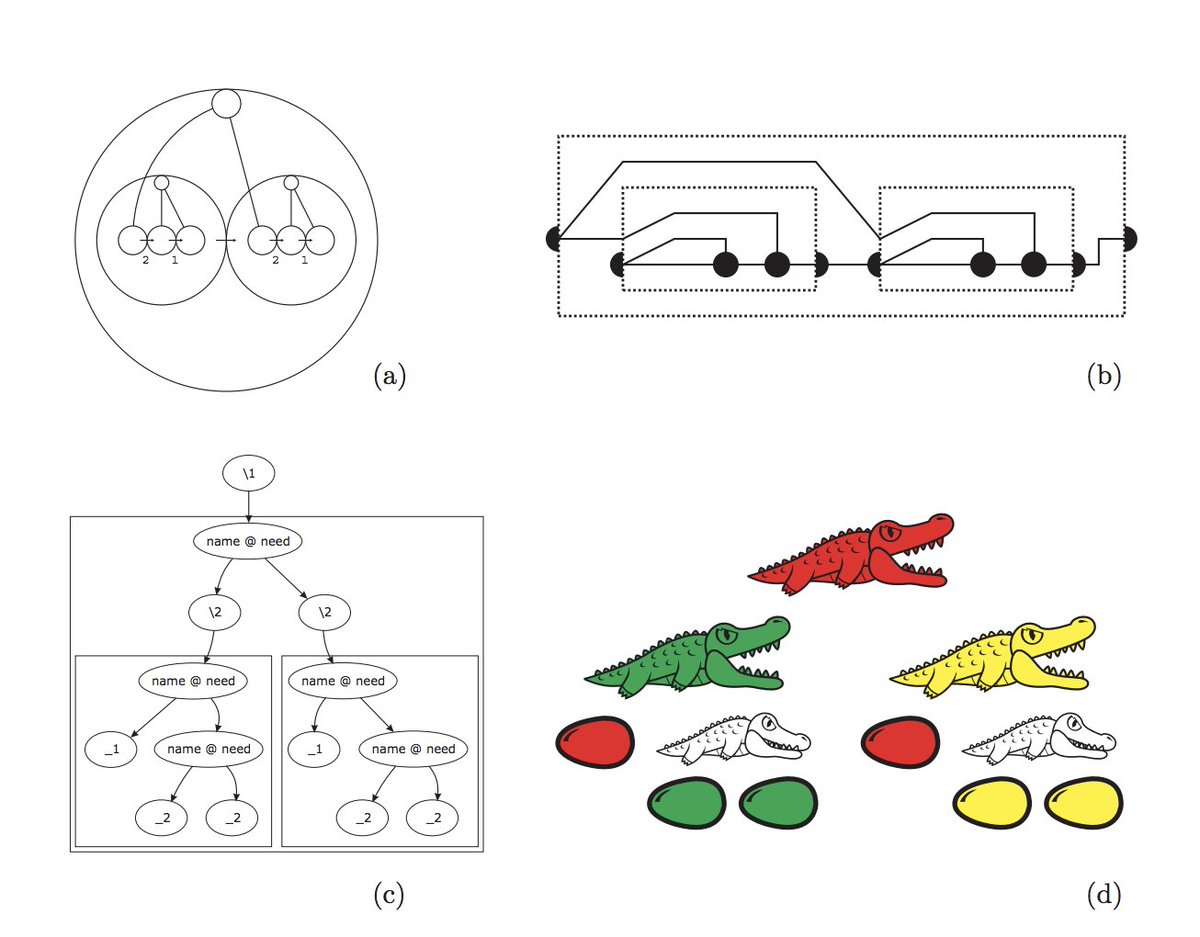
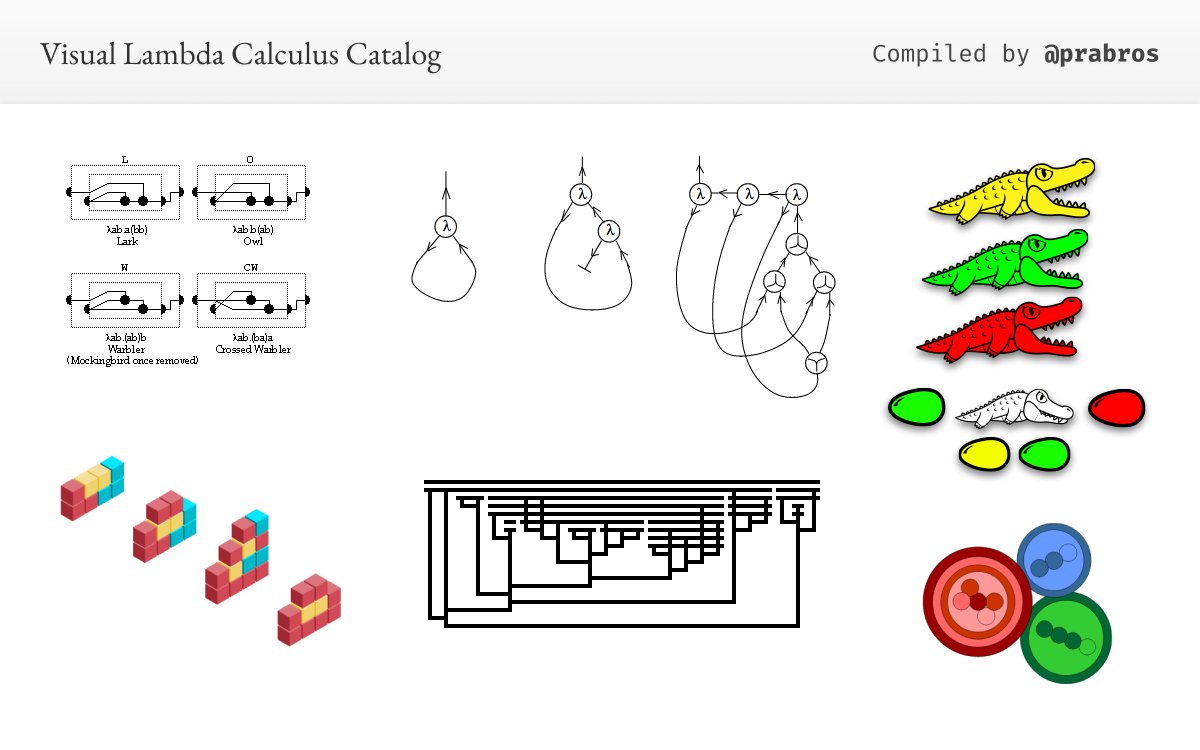
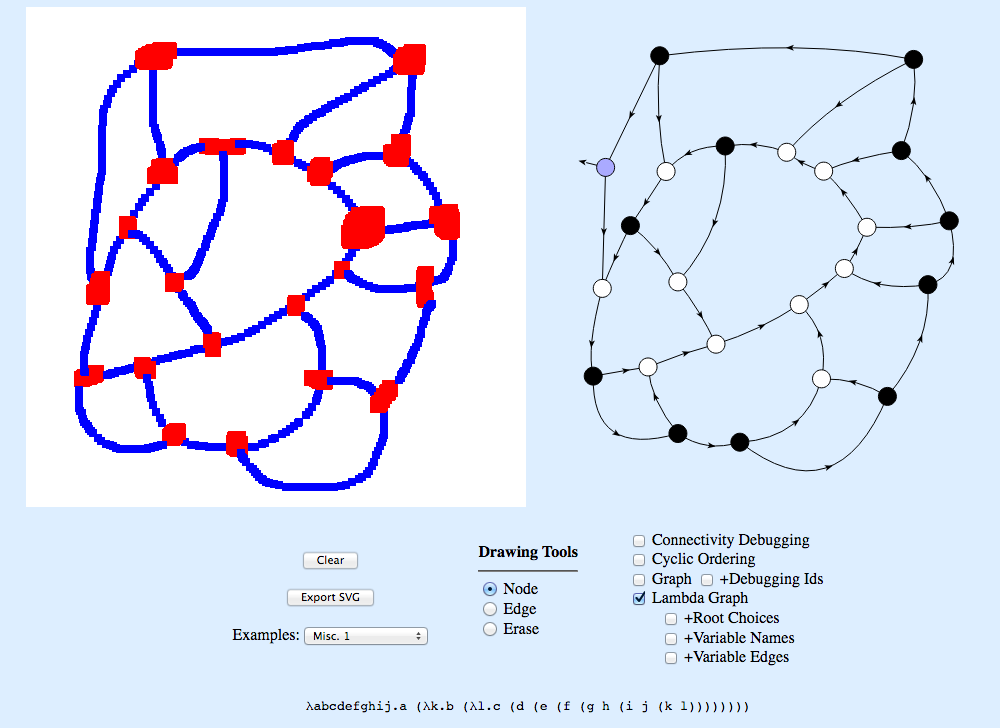
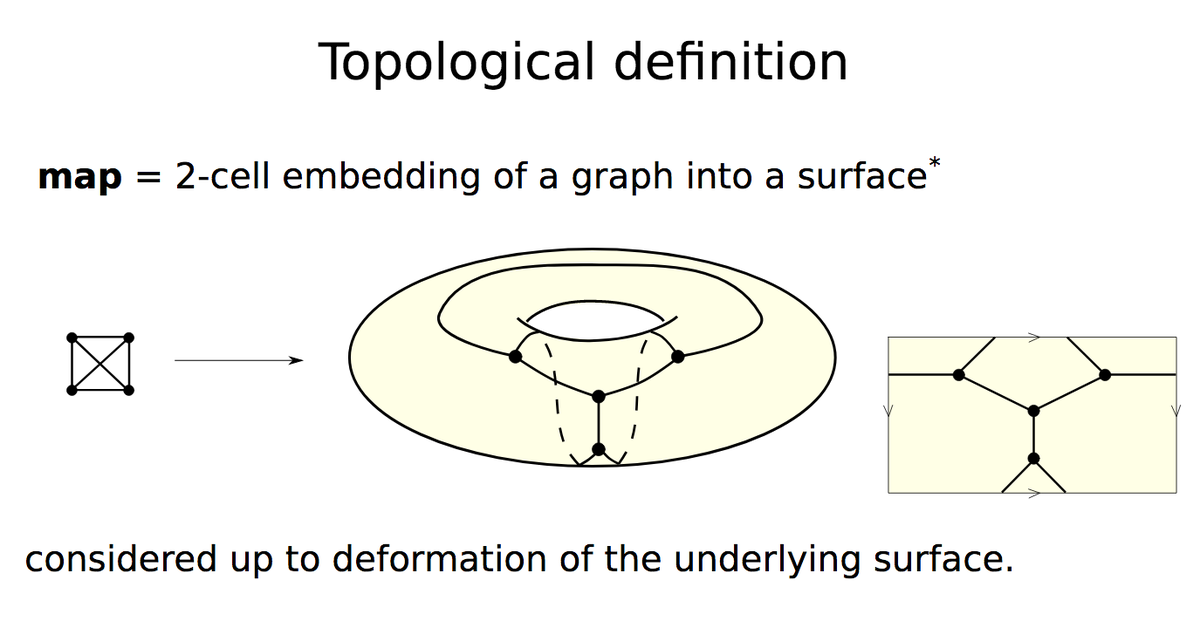
I had visualized Lambda terms as trees earlier:

https://twitter.com/prathyvsh/status/1260778160674664449

but this is a richer representation as maps connect lambda functions with topology.

Second slide from @noamzoam: noamz.org/talks/syco5.20…

Started reading @garlandus’ essay on Hilbert’s role in setting the stage for breakthroughs in computation: archive.is/yxeIm It is a less emphasized perspective and Garlandus does a great job in describing this.

I did a review of another one here:

https://twitter.com/prathyvsh/status/1275137413510164481

The title is from a famous quote by Hilbert where he outlined the formalist program. Article takes a close look at the contributions of Hilbert that lead to Gödel’s Theorem, framing of effective calculability, Category Theory, and their eventual applications in Computer Science.

Hilbert’s work starting out with invariant theory is outlined. An interesting idea here is how Hilbert thought of mathematical theories are going through successive stages of naïve, the formal, and the critical. This is an interesting way to evaluate any nascent field of enquiry.

There are 2 kinds of proofs: Existence proof and Constructive proof. Former establishes existence of an object and the latter describes how to construct what is said to exist. Classicists vs. Intuitionists are divided on this. Hilbert as a traditionalist valued existence proofs.

The idea of constancy vs. variability is a deep domain of study in Mathematics. Their appearance in the presence of the other gives rise to structure and morphism.

Study of invariance bore fruit in multiple domains: Erlangen program characterizes geometry by invariant group transformations, Einstein’s special theory of relativity uses invariant theory of group of Lorentz transformations, and resulted in advances in modern algebra:

Hilbert’s career at Göttingen is described up next. He is said to be popular among his students even though Felix Klein found him as “the most difficult person of all”:

The thinking and working style of Hilbert is detailed here. He had to work and reason out all the things for himself and he did so by going to the bottom of things:

After working on invariants, Hilbert moved on to formalize the work of Euclid. Moving away from the original Greek meaning of “axiom” (self-evident), he built a formalist system that can deduce the theorems from postulates. This is theme from which the titular quote is derived.

@garlandus Learnt that Poincaré termed Peano’s work on setting mathematics on formalist footings as “Pasigraphy”. His work and notation was later adopted by Russell and Whitehead in their magnum opus Principia Mathematica.

Second image from Peano’s text: archive.org/details/formul…

Just realized that this GIF can be thought of as a fixed point: Whatever transformations you do to a starting point, you end up at the same point after going through the process.

Got it from:

https://twitter.com/johncarlosbaez/status/1260223837133660160

Hilbert’s work is located as the beginning of the work on metamathematics, though I think, there are precursors to this, at least as far behind as Plato. The rigorous work of symbolically grounded formalism is I think what could be considered as Hilbert’s unique contribution.

The problems curated by Hilbert at the turn of the century paved way for the advancements that resulted in the idea of computation. These would also go on to influence the subsequent course of mathematics in a considerable manner.

Came across this neat 2✕2 of models of computation.

Source: cs.helsinki.fi/u/jllang/Intro…

A useful conceptual map of how different domains of study of computation are related to each other:

Source: cs.helsinki.fi/u/jllang/Intro…

TIL the first monograph on recursion was written by a woman logician called Rózsa Péter in 1951: en.wikipedia.org/wiki/R%C3%B3zs…

She is considered as the founding mother of recursive function theory. Reminisce here: sdsc.edu/ScienceWomen/p…

cc @valeriadepaiva @WomenInLogic1