Thread by @wiredmau5

I never realised the actual meaning of Logarithm and what value it delivered. It was just a bunch of rules I'd memorised, and applied numbly during exams

But WTF is Logarithms? Why is it needed, how did it originate, and more importantly, how is it that we were never taught that humans perceive most of the real world stimulus on a log scale!

I ended up doing some reading and think I found answers to some of the questions above. Here's a thread capturing all of it

If you had to remember just one thing from this thread, it is this - Logarithms is a way to compress information in a meaningful way

If this definition is not readily intuitive, that would make it the three of us - folks from the 16th century, you(the reader), and me from a while back

To understand what Logarithm has to do with compression of information, lets visit 16th century, where it all started

Curiosity of the times

People during the 16th century had directed much of their curiosity towards the heavens and the earth

People were figuring out their place in the grand scheme of things - measuring our world, measuring the orbits of planets, measuring sea distances for navigators

the perimeter of our curiosity had expanded like never before

This naturally led to intensive calculations with the need of thin error margins

The birth of Logarithm

Two people rose to the need, as demanded by the scientific community, to make calculations easier - They were John Napier & Joost Bürgi

Both were contemporaries who came up with their own version of Logarithms independently

Why were calculations so hard

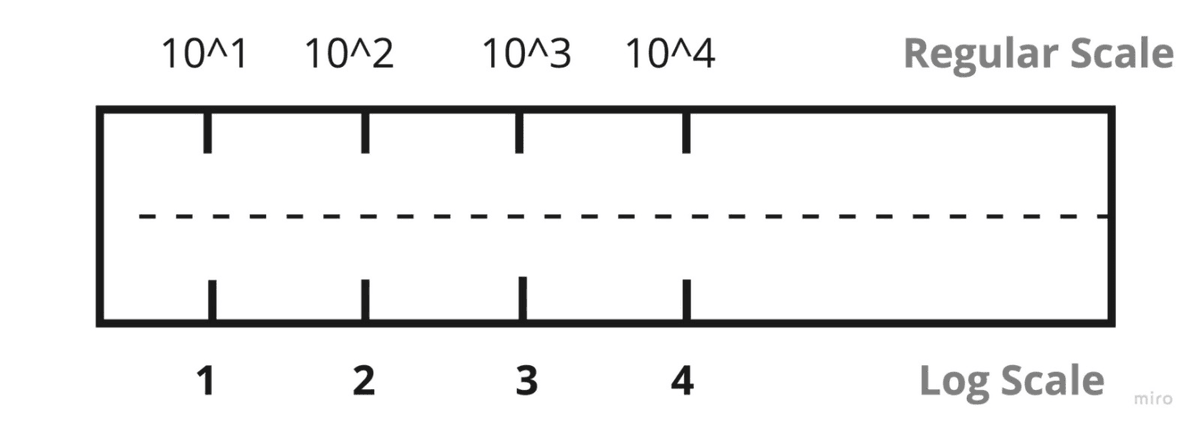
Imagine that you wanted to calculate area of some rectangular land mass with the length and breadth as 10³ units and 10⁴ units

Why should this be hard to calculate, you think, right? Remember, in the 16th century, all they had was pen, paper and a lot of time

Now let's say one fine day, Napier finds you, gives you a scale and asks you to do the following

1. Locate the numbers you wanted to multiply on the regular scale

2. Map the corresponding numbers on the log scale

3. Add them. Yes, add

That would be 7.

Next, he asks you to find 7 on the log scale, and read the corresponding number on the regular scale

That would give you 10⁷, which is the answer you were looking for

*****Powers of 10 were used for simplicity, you could instead use any other pair of numbers like 9³ and 11¹⁵

Take a moment to appreciate how, with the introduction of Log scales, calculations morphed from brutal multiplication into simple addition

This was a phenomenal shift in terms of how people did calculations

No wonder the French mathematician Pierre-Simon Laplace noted that logarithms "by shortening the labours, doubled the life of an astronomer"

If you are wondering how Napier/Joost came up with this scale - they manually calculated them 😳

Napier worked for 20 years to calculate more than 10 million rows to become an overnight success

Changing the scale of observation

So we realise that Logs made calculations easier. How?

By allowing us to compress large numbers to more manageable forms, without any loss of information

Let's take a real world example with a slightly different flavour to understand Logs better

To sense & respond to the natural world has been(and will be) critical to our survival. As we all know, natural world is notoriously random, and creates stimuli with all kinds of intensities

For eg, the natural world gives you the sensory stimulus of buzz of a bee and also the boom of eruption of a volcano - your ears register both!

How we hear is nothing short of an engineering marvel - we can hear an overwhelming range of sounds - we can hear anything from your best friend whispering to the sound of our favourite artist playing live.

If you were to map this range of what all you could hear on a linear scale, it would look like this

But something is odd. On the linear scale, the human ears would not be able to accurately tell apart between a whisper, a normal conversation or a lawn mover

But we know that's not true!
---
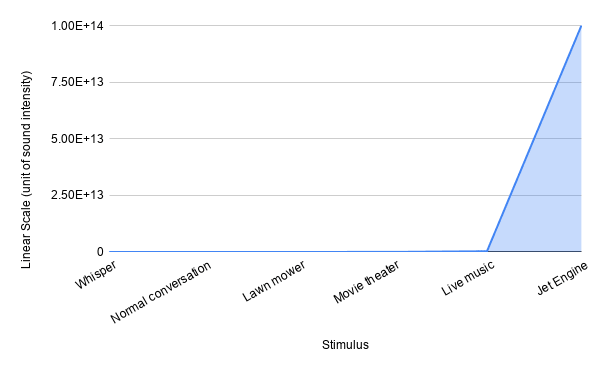
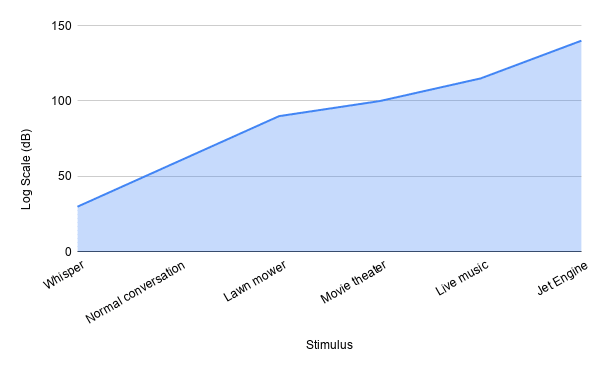
How is this possible? How are we able to differentiate between such wide range of sound intensities?

It is because we perceive sound on a log scale

This is how our ears perceive external stimulus on the log scale

Think about it!

Only because we perceive sound on a log scale, we are able to consume such a wide range of sounds

What's amazing is that this was true even before Napier came up with concept of Logarithms - he stumbled upon Logarithms trying to solve a very different problem

The next time you see observations on a log scale, just remember - It was done to compress information in a way to make it easier for you to consume

Armed with this new intuition, let's revisit another recent real world example - COVID-19.

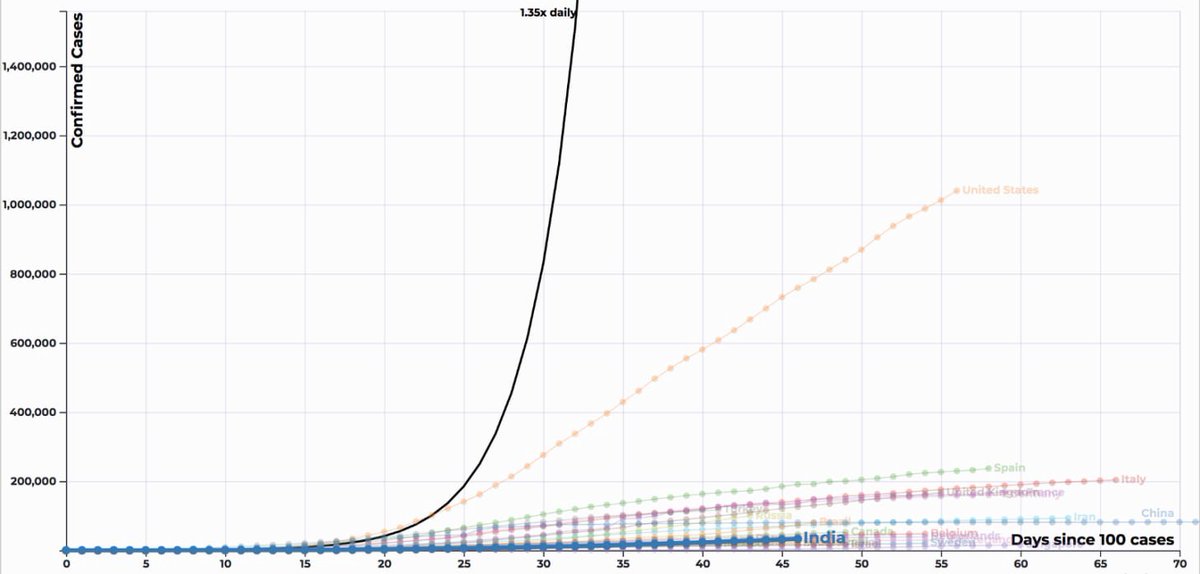
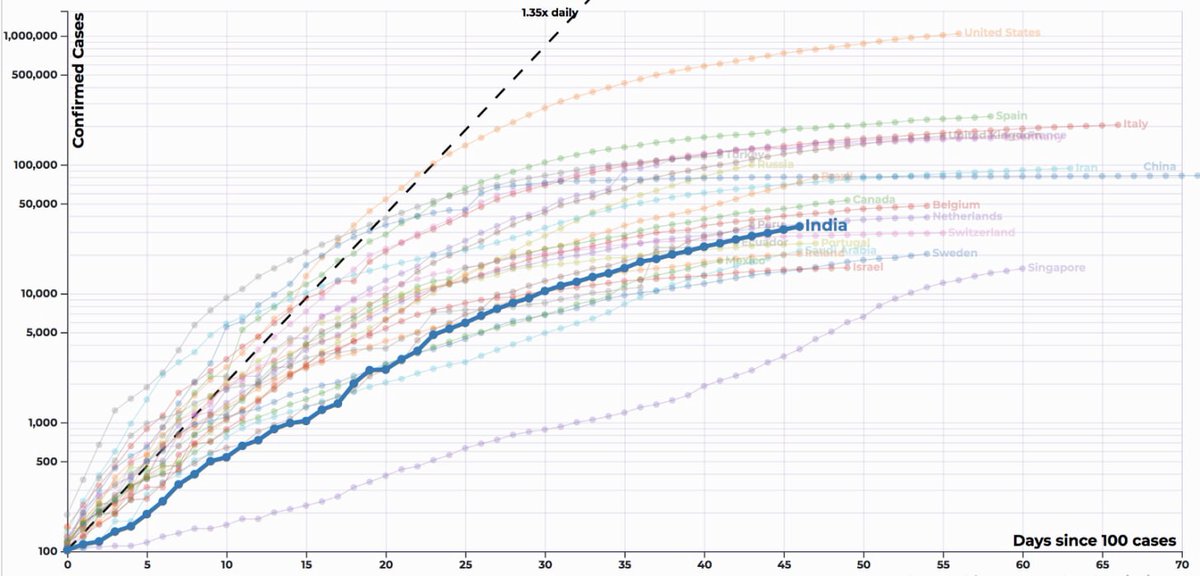
Unfortunate as it is, let's try to make sense of the scale of its impact on major countries around the world

COVID-19 & log scale

Following image shows the "Total no of confirmed cases" on the Y axis and the "No of days since 100 confirmed cases" on the X axis

I have highlighted India (blue, bottom) to indicate the trend. What can you ascertain from this image? Does it give much insight when compared to other countries?

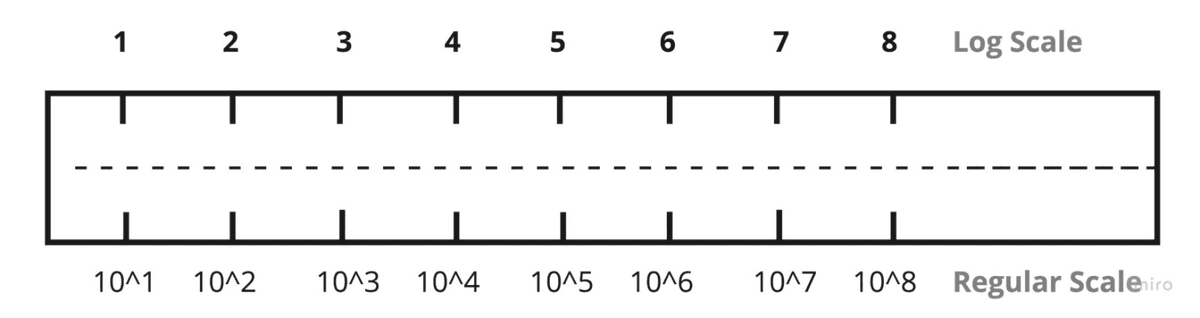
Now, let's use the log scale

We were able to compress the information (no of active cases) to make it easier to consume (and compare)

Note, how the exponential curve(1.3x daily) from the linear scale resolves into a pretty straight line - Neat demonstration of how information (things growing exponentially) get compressed (things growing linearly) so that you can consume & compare the information better

This is the power of Logs, and not Log(A*B) = Log(A)+Log(B).

Screw school curriculum

PS : The COVID-19 data can be found here (91-divoc.com/pages/covid-vi…) built by @profwade_ . Highly recommended!

So, in conclusion

Logarithms is a way to compress information that makes it easier to consume and compare - it is a shame that we were taught logarithms in a way bereft of this beautiful intuition

I would encourage you to read the fantastic article titled "Why do we perceive Logarithmically" to understand how we humans evolved with our perceptions attuned to a log scale, so that we could make more sense of this vast and beautiful world

rss.onlinelibrary.wiley.com/doi/pdf/10.111…

Feedback/Questions? Leave a comment

Thanks for reading!

Phew