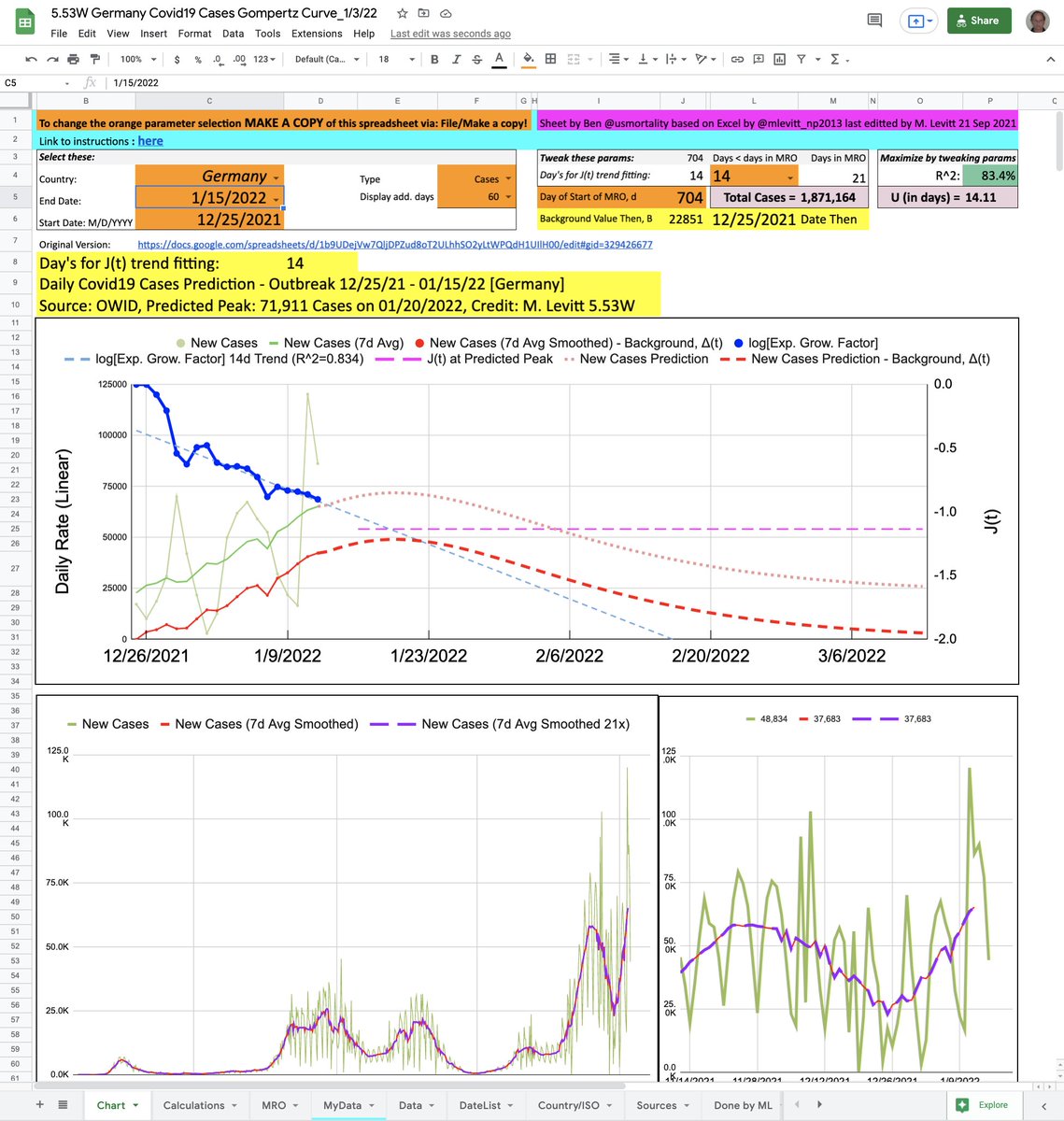
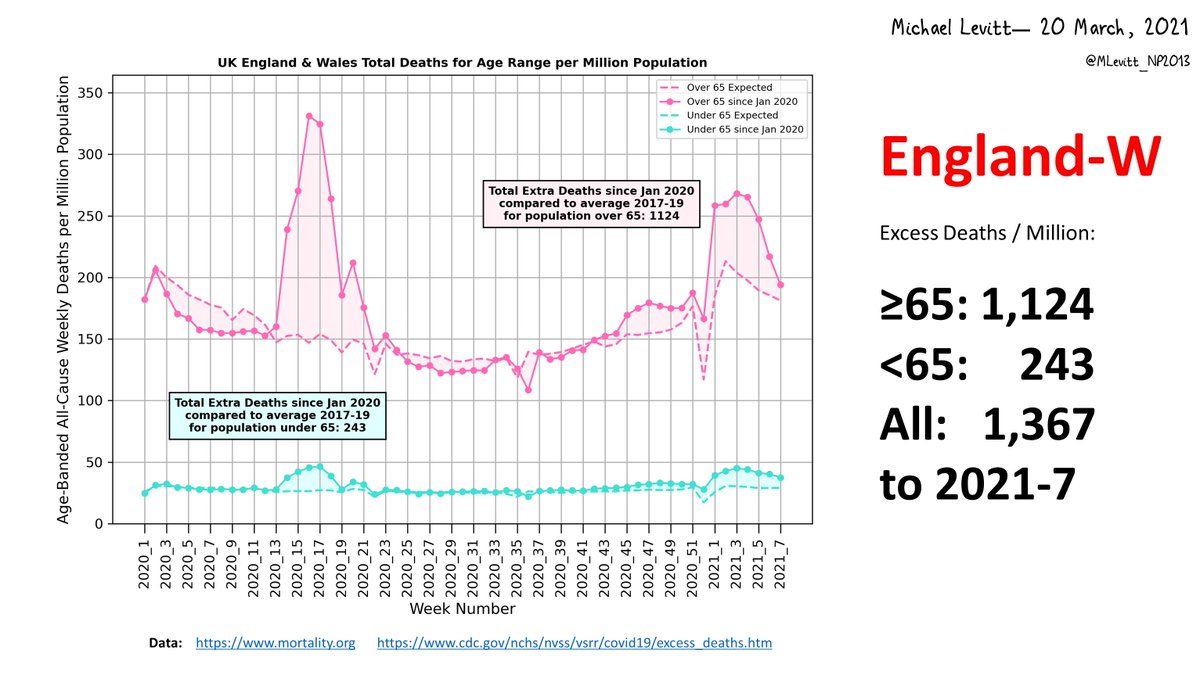
@EdConwaySky @benton328 @phil_luttazi @KielRobinson @CeeMacBee @ScottGottliebMD @CT_Bergstrom @BuckSexton @nataliexdean @sav_says_ @JamesOKeefeIII @NAChristakis Europe's COVID19 Excess Deaths plateau at 153,006, 15% more than 17/18 Flu with same age range counts. Details follow 







EuroMOMO euromomo.eu/graphs-and-maps Excess Deaths from 2020 Week 8 now match reported COVID Deaths @JHUSystems perfectly (better than 2%). In earlier weeks the reported deaths were lower. Not sure why? It allows me to do this in depth analysis & comparison with EuroMOMO influenza. 

Analysis of Europe's Excess Deaths is hard: EuroMOMO provides beautiful plots; data requires hand-recorded mouse-overs. COVID19 2020, Weeks 08-19 & flu 2018, Weeks 01-16 is relatively easy for all age ranges (totals 153,006 & 111,226). Getting Dec. 2017 flu peak is very tricky. 

Should be easy as mouse over gives two values a week: Actual death count & Baseline value. Tests on COVID19 peak gave total of 127,062 deaths & not 153,006. Plotting table & superimposing real plot showed why. Wrong Baseline values are actually 'Substantial increase' values!! 





Requiring two COVID19 death counts to match means reducing Baseline value by 23,774/12=1,981. Mouse-over 2017 weeks 46 to 52 gave table below. Negative excess death meant 2017 flu began Week 49 not 46. We tried to get Age Range data for 2017 but table just use 2018 flu data. 





• • •
Missing some Tweet in this thread? You can try to
force a refresh