Share this page!

Enter URL or ID to Unroll

You can paste full URL like: https://x.com/threadreaderapp/status/1644127596119195649
or just the ID like: 1644127596119195649

How to get URL link on X (Twitter) App

  1. On the Twitter thread, click on or icon on the bottom
  2. Click again on or Share Via icon
  3. Click on Copy Link to Tweet
  4. Paste it above and click "Unroll Thread"!
  5. More info at Twitter Help
Michael Levitt Profile picture
@MLevitt_NP2013
May 27, 2020 • 4 tweets • 4 min read • Read on X
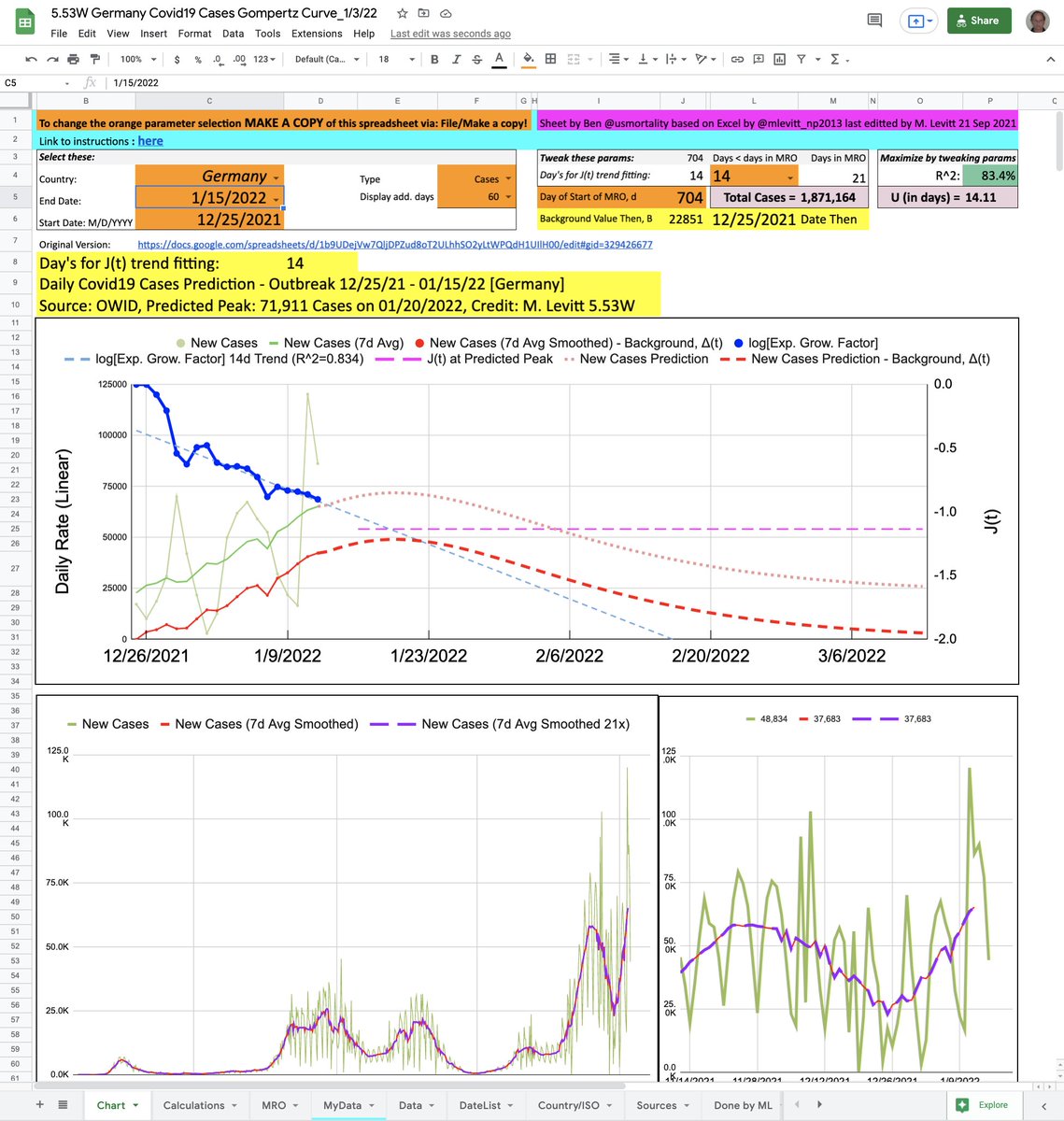
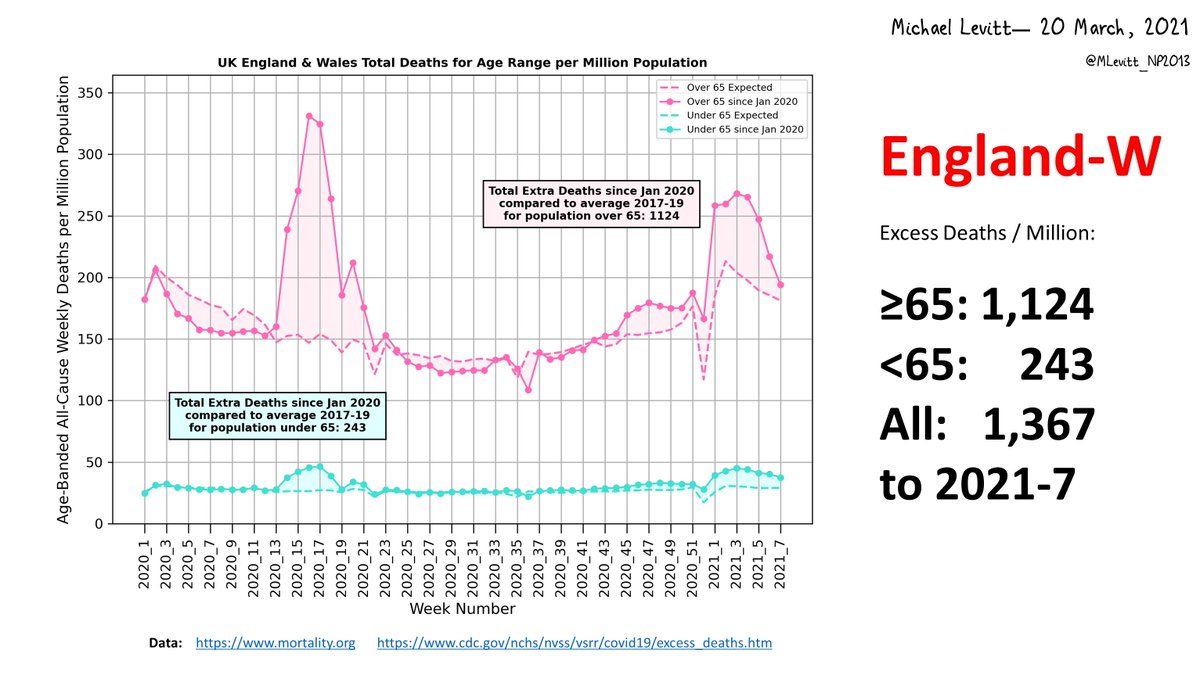
Here is my clearer analysis of the Population Fatality Rate (PFR) related to influential predictions by Ferguson et al. 2020. It use data released by the Chinese CDC on 14Apr20 @ChinaCDCWeekly, not full-text indexed by Google @Google but released in The @guardian on 1Mar20. ImageImageImage
Here is the evidence showing Google still does not full-text index this essential report. The Guardian @guardian finally gave CCDC @chinacdc age-range death numbers on 1 Apr. weekly.chinacdc.cn/en/article/id/…
theguardian.com/world/2020/mar… Vulnerability of OLDER people is not even headlined! ImageImageImage
A perceptive reader will ask for the Verity et al., 2020 IFR. My 25Mar report to UK scientific leaders used that data. After normalization to percent, Verity IFR data is identical (0.6% RMSD) to deaths/Chinese_population in Col. F on Tweet1 Excel. My numbers are unchanged. ImageImageImage
This analysis has been extraordinarily interesting. I will write it up as a PDF report with the Excel and also make a video today. Just shows that we can learn from every question and critique.

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Michael Levitt

Michael Levitt Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @MLevitt_NP2013

Michael Levitt Profile picture
Jan 16, 2022
Just so Europe does not feel left out, here are some of the larger countries.

All use the same 5.5W sheet
docs.google.com/spreadsheets/d…

Spain 133,000 cases/day at peak on 12-Jan.
docs.google.com/spreadsheets/d…
Italy 181,000 cases/day on peak on 13-Jan.

docs.google.com/spreadsheets/d…
Germany 72,000 cases/day on peak on 20-Jan.

This new Omicron outbreak comes on the heels of previous outbreak (Delta? that peaked 25-Nov-21). Set start to 25-Dec, later that with 13-Dec. start.

Anyone know if outbreaks in different places like Holland
Read 5 tweets
Michael Levitt Profile picture
Jan 16, 2022
USA Omicron has peaked. Daily new cases on the decline.

Open Sheet:
docs.google.com/spreadsheets/d…
Big states looking good too.

California 130K cases/day at peak on 19-Jan.

docs.google.com/spreadsheets/d…
Florida 59K cases/day at peak on 7-Jan.

docs.google.com/spreadsheets/d…
Read 5 tweets
Michael Levitt Profile picture
Aug 8, 2021
As someone who broke the news to Israeli leaders on Sweden’s handling of COVID-19 in Mar. 2020, I am so distressed to be reading this now m.ynet.co.il/articles/hj30k…

When will Homo Sapiens realize that we can never stop a tiny virus & re-engineer human biology by force not smarts?
Please note that the two translation are automatic. I give independent results from Microsoft and Google. The original is in Hebrew.

Taking this opportunity to rejoice in machine translation. It it so worthwhile to get used to its quirks.
Fortunately age-adjusted excess death in Israel for the 75 weeks from 1-Jan-20 to 6-Jun-21 is almost as small as that in Sweden (<2% of natural death in 75 weeks)

Economic, social, medical & educational cost to Israel likely higher than to Sweden.

Does anyone have good data?
Read 5 tweets
Michael Levitt Profile picture
Jul 11, 2021
1/n
 Growth of COVID-19 outbreaks may seems specialized, but is crucially important.

If growing by commonly used Logistic function, early growth is exponential & forecast of outcome is impossible.

For Gompertz function, growth is slowing from start allowing forecast of end.
2/n
 Described on YouTube year ago, this is still not widely understood


Then we focused on small outbreaks (1000's cases) well-contained in New Zealand and South Korea.

Stimulated by @Marco_Piani & @PienaarJm, we now analyze Lompardy, NYC, UK & Spain.
3/n
 Before releasing results & Excel fits, I describe the growth functions and then show raw data.

If you want to learn about growth functions, study the properties of the functions so that you can identify how the real data changes.

I got this wrong from 1-Feb-20 to 20-Mar-20. Image
Read 4 tweets
Michael Levitt Profile picture
May 30, 2021
I am sure that there will be something that correlates with COVID19 death rate better that the stringency of restrictions.

Finding it is important!

The entire world needs to know what to do the next time there is a serious viral threat.
1/8
 Interesting replies led me to carefully analyze data in @youyanggu GitHub table. Alway more objective when one collects data, another analyses it.

Looking at data so first tidy table in Excel.

Color formatting is red-yellow-green low value to high. Image
2/8
 Rather than make plots of one measure against another, we get the correlation coefficient of all pairs of measures.

Correlation coefficient, CC, of A to B is same as CC of B to A so table is symmetric. Correlation coefficient of A to A is always 1; it is whited out here. Image
Read 9 tweets
Michael Levitt Profile picture
Mar 21, 2021
1/7
 Excess death (E) in any period is the difference between the actual all-cause deaths and those that are expected. Expected deaths in the current year, c, can be calculated in many ways. Easiest is to use the data from a few recent years as a reference (we use, 2017 to 2019).
2/7
 Data can be used in 3 ways to calculate expected deaths.
(1) as average death in the reference years.
(2) as average corrected for the change in total population.
(3) as average for each age band corrected for its population, what we call age-adjusted.

We use 5 age bands.
3/7
 (1) If D(i) is death in reference years i, then expected death in year c is E(c)=average[D(i)].
(2) If P(i) is population; E(c)=P(c)*average[D(i)/P(i)].
(3) If (P(i,j) is population of age band j in year i, D(i,j) the corresponding death; E(c,j)=P(c,j)*average[D(i,j)/P(i,j)]
Read 7 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us!

Send Email!

:(