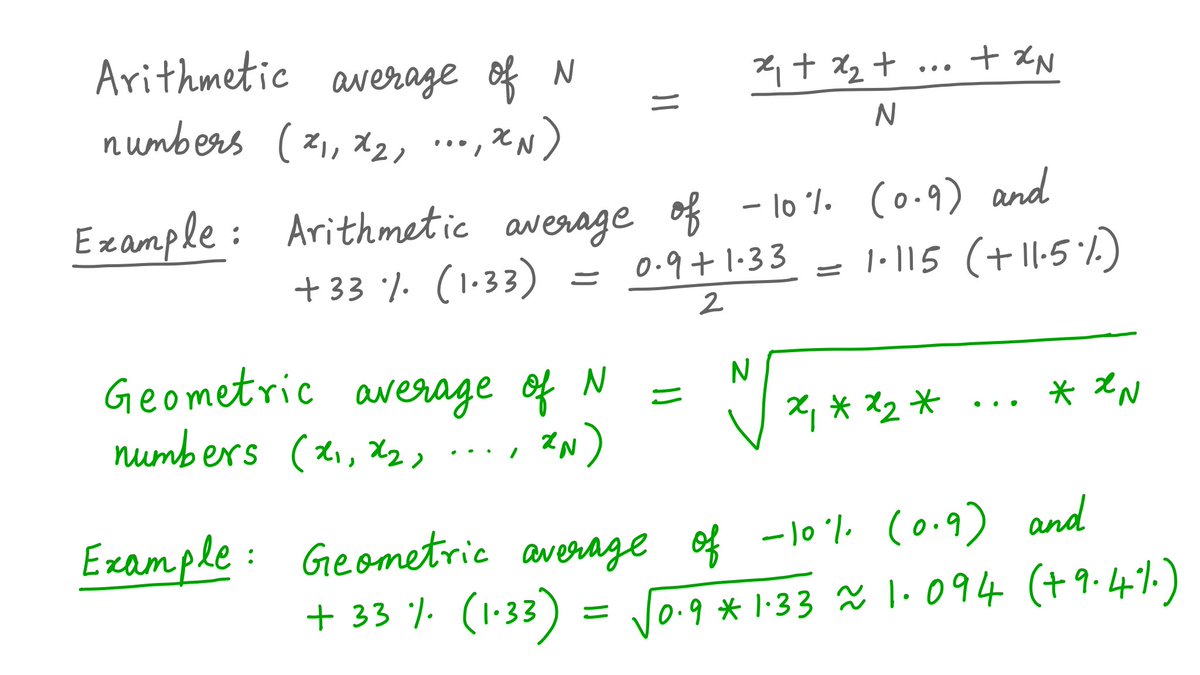Get a cup of coffee.
In this thread, I'll show you why "geometric thinking" is superior to "arithmetic thinking" while making investment decisions.
Let's start with an example.
There are 2 stocks, A and B.
A goes up 10% every year. Like clockwork.
B is more volatile. Half the years, it goes down 10%. But the other half, it compensates by going up 33%.
You have $10,000.
You have to pick a stock (A or B), put your entire $10K in it, and not touch it for 20 years.
Do you pick A or B?
Some mental math for Option B: half the years, B is down 10%. The other half, it's up 33%. On average, that's a 11.5% return, right? After all, (-10% + 33%)/2 = 11.5%.
That seems better than Option A's steady 10%.
So you should pick B over A, right?
Read on.
Say you choose Option B. You put your $10K in stock B. You hold for 20 years.
As advertised, B goes up 33% during 10 of those years, and down 10% during the other 10.
How much are you left with?
That's easy. You'd have $10K*(0.9^10)*(1.33^10) = $60,387.
Not bad.
If instead, you'd been a sucker and taken Option A's steady 10%, how much would you have?
Even easier. $10K*(1.1^20) = $67,275.
Wait, Option A gets you $6,888 *more* than Option B?
How's that possible?
The reason is: "arithmetic thinking" vs "geometric thinking".
Let me explain. How did we calculate the average 11.5% return for Option B?
We just took the average of -10% and +33%. (-10% + 33%)/2 = +11.5%. That's "arithmetic".
But how did the $10K invested in B actually behave?
Half the years (-10%), it got multiplied by 0.9. And the other half (+33%), it got multiplied by 1.33.
That's a growth rate of ((0.9^10)*(1.33^10))^(1/20), or 9.4%. Not 11.5%.
This 9.4% is the *geometric* average of -10% and +33%. The 11.5% was their *arithmetic* average.
To many people, average just means arithmetic average.
But if you make investment decisions all day long, you probably encounter geometric averages far more often.
Key lesson: Money does not grow arithmetically. It compounds geometrically.
So, when you make investment decisions, "geometric thinking" is superior to "arithmetic thinking".
Here's an interesting mathematical fact:
The geometric average of any N positive numbers *never* exceeds their arithmetic average.
This is called the "Arithmetic Mean/Geometric Mean theorem", or the "AM/GM theorem" for short.
en.wikipedia.org/wiki/Inequalit…
You may have noticed that I said "positive numbers" in the theorem above.
But don't worry. When we work with money, our numbers are always positive. Even a negative 10% return is just multiplication by 0.9, a positive number.
So the theorem always applies.
The AM/GM theorem means:
If you approximate annual returns by taking their arithmetic average, you will always *overestimate* your actual return.
So, arithmetic thinking is not just wrong. It's dangerous. It makes you think you'll have more money than you'll actually do.
Think about what this means for pension funds and 401-Ks that assume a steady 7% return.
If the fund loses money some years and makes it up in others, it may do worse than 7% long term.
And AM/GM *guarantees* it, if the average arithmetic annual return is 7%.
Humans are wired so that geometric thinking is much harder for most people than arithmetic thinking.
If you cultivate geometric thinking, you'll have an edge over most people.
Yes, geometric calculations are hard.
And we're not Buffett. Most of us can't do geometric averages in our heads.
But we're surrounded by calculating machines. Smartphones. Tablets. Laptops. Excel. Python.
No excuse for not using them while taking important decisions.
Thanks for reading. Enjoy your weekend. Be safe. Think geometric.😀
/End